Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T21:56:35.928Z Has data issue: false hasContentIssue false
  • English
  • Français

On the 2-Rank of the Hilbert Kernel of Number Fields

Published online by Cambridge University Press:  20 November 2018

Ross Griffiths  and
Mikaël Lescop
Ross Griffiths
Affiliation:
Department of Mathematics and Statistics, McMaster University, 1280 Main StreetWest, Hamilton, Ontario L8S 4K1, e-mail: [email protected]
Mikaël Lescop
Affiliation:
IUT de Brest, Départment GMP, Rue de Kergoat, 29200 Brest, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 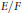$E/F$ be a quadratic extension of number fields. In this paper, we show that the genus formula for Hilbert kernels, proved by M. Kolster and A. Movahhedi, gives the 2-rank of the Hilbert kernel of $E$ provided that the 2-primary Hilbert kernel of $F$ is trivial. However, since the original genus formula is not explicit enough in a very particular case, we first develop a refinement of this formula in order to employ it in the calculation of the 2-rank of $E$ whenever $F$ is totally real with trivial 2-primary Hilbert kernel. Finally, we apply our results to quadratic, bi-quadratic, and tri-quadratic fields which include a complete 2-rank formula for the family of fields 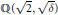$\mathbb{Q}(\sqrt{2},\sqrt{\delta )}$ where 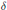$\delta $ is a squarefree integer.

Keywords

11R7019F15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 5 , 01 October 2009 , pp. 1073 - 1091
Copyright
Copyright © Canadian Mathematical Society 2009

References

[BC] Barrucand, P. and Cohn, H., Note on primes of type x 2 + 32y 2, class number, and residuacity. J. Reine Angew. Math. 238(1969), 67–70.Google Scholar
[BS] Browkin, J. and Schinzel, A., On Sylow-2 subgroups of K 2(OF) for quadratic number fields F. J. Reine Angew. Math. 331(1982), 104–113.Google Scholar
[CW] Chase, S. U. and Waterhouse, W. C., Moore's theorem on uniqueness of reciprocity laws. Invent. Math. 16(1972), 267–270.Google Scholar
[Ga] Garland, H., A finiteness theorem for K 2 of a number field. Ann. of Math. 94(1971), 534–548.Google Scholar
[Gr1] Griffiths, R., Multi-Quadratic Extensions of Q with Trivial 2-Primary Hilbert Kernel. Master’s thesis, Mc Master University, 2000.Google Scholar
[Gr2] Griffiths, R., A genus formula for étale Hilbert kernels in a cyclic p-power extension. Ph.D. thesis, Mc Master University, 2005.Google Scholar
[JSG] Jaulent, J.-F. and Soriano-Gafiuk, F., 2-Groupe des classes positives d’un corps de nombres et noyau sauvage de la K 2-théorie. J. Number Theory 108(2004), no 2, 187–208.Google Scholar
[Ka] Kahn, B., Descente galoisienne et K 2 des corps de nombres. K -theory 7(1993), 55–100.Google Scholar
[Ke] Keune, F., On the structure of the K 2 of the ring of integers in a number field. K -Theory 2(1989), no. 5, 625–645.Google Scholar
[K M] Kolster, M. and Movahhedi, A., Bi-quadratic number fields with trivial 2-primary Hilbert kernel. Proc. London Math. Soc. 87(2003), no. 1, 109–136.Google Scholar
[L1] Lescop, M., Sur les 2-extensions de Q dont la 2-partie du noyau sauvage est triviale. Thèse, Universit é de Limoges, 2003.Google Scholar
[L2] Lescop, M., 2-extensions of Q with trivial 2-primary Hilbert kernel. Acta Arith. 112(2004), no. 2, 345–366.Google Scholar
[Mi] Milnor, J., Introduction to Algebraic K-Theory. Annals of Mathematics Studies 72, Princeton University Press, Princeton, NJ, 1971.Google Scholar
[N] Neukirch, J., Class Field Theory. Grundlehren der Mathematischen Wissenschaften 280, Springer-Verlag, Berlin, 1986.Google Scholar
[T] Tate, J., Relations between K 2 and Galois cohomology. Invent. Math. 36(1976), 257–274.Google Scholar