Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T12:00:59.222Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some Twisted Chevalley Groups Over Laurent Polynomial Rings

Published online by Cambridge University Press:  20 November 2018

Jun Morita
Jun Morita*
Affiliation:
University of Tsukuba, Ibaraki, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We let Z denote the ring of rational integers, Q the field of rational numbers, R the field of real numbers, and C the field of complex numbers.

For elements e and f of a Lie algebra, [e,f] denotes the bracket of e and f. A generalized Cartan matrix C = (cij) is a square matrix of integers satisfying cii = 2, cij ≦ 0 if i ≠ j, cij = 0 if and only if cji = 0. For any generalized Cartan matrix C = (cij) of size l × l and for any field F of characteristic zero, 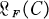denotes the Lie algebra over F generated by 3l generators e1, …, el, h1, …, hl, f1, …, fl with the defining relations

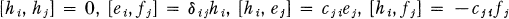
for all i, j,

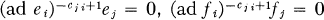
for distinct i, j.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 5 , 01 October 1981 , pp. 1182 - 1201
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Abe, E., Coverings of twisted Chevalley groups over commutative rings, Sci. Rep. Tōkyō Kyōiku Daigaku 13 (1977), 194–218.Google Scholar
2. Bourbaki, N., Groupes et algèbres de Lie, Chap. 4-6 (Hermann, Paris, 1968).Google Scholar
3. Humphreys, J. E., Introduction to Lie algebras and representation theory, (Springer, Berlin, 1972).Google Scholar
4. Iwahori, N., On the structure of a Hecke ring of a Chevalley group over a finite field, J. Fac. Sci., Univ. of Tokyo 10 (1964), 215–236.Google Scholar
5. Kac, V. G., Simple irreducible graded Lie algebras of finite growth, Math. USSR-Izvestija 2 (1968), 1271–1311.Google Scholar
6. Kac, V. G., Automorphisms of finite order of semisimple Lie algebras, Functional Anal. Appl. 3 (1969), 252–254.Google Scholar
7. Macdonald, I. G., Affine root systems and Dedekind's η-functions, Inventiones Math. 15 (1972), 91–143.Google Scholar
8. Moody, R. V., Euclidean Lie algebras, Can. J. Math. 21 (1969), 1432–1454.Google Scholar
9. Moody, R. V., Simple quotients oj'Euclidean Lie algebras, Can. J. Math. 22 (1970), 839–846.Google Scholar
10. Moody, R. V. and Teo, K. L., Tits’ systems with crystallo graphic Weyl groups, J. Algebra 21 (1972), 178–190.Google Scholar
11. Morita, J., Tits1 systems in Chevalley groups over Laurent polynomial rings, Tsukuba J. Math. 3 (1979), 41–51.Google Scholar
12. Steinberg, R., Lectures on Chevalley groups, Yale Univ. Lecture Notes (1967/68).Google Scholar
13. Teo, K. L., Simple quotients of the three tiered Euclidean Lie algebra, Bull. London Math. Soc. 9 (1977), 299–304.Google Scholar