Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T01:35:09.111Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some Exponential Equations of S. S. Pillai

Published online by Cambridge University Press:  20 November 2018

Michael A. Bennett
Michael A. Bennett*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

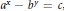In this paper, we establish a number of theorems on the classic Diophantine equation of S. S. Pillai, ${{a}^{x}}-{{b}^{y}}=c$ , where 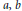$a,\,b$ and $c$ are given nonzero integers with 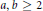$a,\,b\,\ge \,2$. In particular, we obtain the sharp result that there are at most two solutions in positive integers 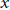$x$ and $y$ and deduce a variety of explicit conditions under which there exists at most a single such solution. These improve or generalize prior work of Le, Leveque, Pillai, Scott and Terai. The main tools used include lower bounds for linear forms in the logarithms of (two) algebraic numbers and various elementary arguments.

Keywords

11D6111D4511J86
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 5 , 01 October 2001 , pp. 897 - 922
Copyright
Copyright © Canadian Mathematical Society 2001

References

[BS] Beukers, F. and Schlickewei, H. P., The equation x + y = 1 in finitely generated groups. Acta Arith. (2) 78(1996), 189–199.Google Scholar
[Ca] Cassels, J. W. S., On the equation ax – by = 1 . Amer. J. Math. 75(1953), 159–162.Google Scholar
[Ch] Chein, E. Z., Some remarks on the exponential diophantine equation. Notices Amer. Math. Soc. 26(1979), A–426, A-427.Google Scholar
[FA] Fielder, D. C. and Alford, C. O., Observations from computer experiments on an integer equation. In: Applications of Fibonacci numbers, Vol. 7 (Graz, 1996), Kluwer Acad. Publ., Dordrecht, 1998, 93–103.Google Scholar
[He] Herschfeld, A., The equation 2 x – 3 y = d. Bull. Amer.Math. Soc. 42(1936), 231–234.Google Scholar
[Kh] Khinchin, A. Y., Continued Fractions. 3rd edition, P. Noordhoff Ltd., Groningen, 1963.Google Scholar
[Le] Le, M., A note on the diophantine equation axm – byn = k. Indag. Math. (N.S.) 3(1992), 185–191.Google Scholar
[Lev] Leveque, W. J., On the equation ax – by = 1 . Amer. J. Math. 74(1952), 325–331.Google Scholar
[Mi] Mignotte, M., A corollary to a theorem of Laurent-Mignotte-Nesterenko. Acta Arith. 86(1998), 101–111.Google Scholar
[Mi2] Mignotte, M., Catalan's equation just before 2000. Preprint.Google Scholar
[MP] Mignotte, M. and Pethő, A., On the Diophantine equation xp – x = yq – y. Publ. Math. 43(1999), 207–216.Google Scholar
[Mo] Mordell, L. J., On the integer solutions of y(y + 1) = x(x + 1)(x + 2). Pacific J. Math. 13(1963), 1347–1351.Google Scholar
[Pi1] Pillai, S. S., On the inequality 0 < ax – by ≤ n. J. Indian Math. Soc. 19(1931), 1–11.Google Scholar
[Pi2] Pillai, S. S., On ax – by = c. J. Indian Math. Soc. (N.S.) 2(1936), 119–122, and 215.Google Scholar
[Pi3] Pillai, S. S., On ax – bY = by ± ax . J. Indian Math. Soc. (N.S.) 8(1944), 10–13.Google Scholar
[Pi4] Pillai, S. S., On the equation 2 x – 3 y = 2 X + 3 Y . Bull. Calcutta Math. Soc. 37(1945), 18–20.Google Scholar
[Pin] Pintér, Á., On a diophantine problem of P. Erdoʺs. Arch. Math. 61(1993), 64–67.Google Scholar
[Po] Pólya, G., Zur Arithmetische Untersuchung der Polynome. Math. Z. 1(1918), 143–148.Google Scholar
[Ri] Ribenboim, P., Catalan's Conjecture. Academic Press, London, 1994.Google Scholar
[Sc] Scott, R., On the equations px – by = c and ax + by = cz . J. Number Theory 44(1993), 153–165.Google Scholar
[Sh] Shorey, T. N., On the equation axm – byn = k. Indag. Math. 48(1986), 353–358.Google Scholar
[ShTi] Shorey, T. N. and Tijdeman, R., Exponential Diophantine Equations. Cambridge, 1986.Google Scholar
[StTi] Stroeker, R. J. and Tijdeman, R., Diophantine Equations. In: Computational Methods in Number Theory, Math. Centre Tracts 155, Centr. Math. Comp. Sci., Amsterdam, 1982, 321–369.Google Scholar
[Te] Terai, N., Applications of a lower bound for linear forms in two logarithms to exponential Diophantine equations. Acta Arith. 90(1999), 17–35.Google Scholar
[Ti] Tijdeman, R., On the equation of Catalan. Acta Arith. 29(1976), 197–209.Google Scholar