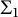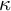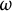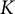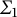1 Introduction
The concepts of closed unbounded and stationary subsets capture many of the key aspects of the combinatorics of cardinals of uncountable cofinalities. Recent developments in the study of canonical inner models of set theory provide strong motivations for analyzing the definability – specifically, the ordinal definability – of these objects. In particular, the notion of a
![]() $\omega $
-strongly measurable cardinal
$\omega $
-strongly measurable cardinal
![]() $\kappa $
in
$\kappa $
in
![]() $\mathrm {{HOD}}$
, introduced by Woodin (see [Reference H. Woodin21, Definition 189]) to measure local failures of the inner model
$\mathrm {{HOD}}$
, introduced by Woodin (see [Reference H. Woodin21, Definition 189]) to measure local failures of the inner model
![]() $\mathrm {{HOD}}$
to approximate the set-theoretic universe V, is equivalent to the fact that the restriction of the closed unbounded filter on
$\mathrm {{HOD}}$
to approximate the set-theoretic universe V, is equivalent to the fact that the restriction of the closed unbounded filter on
![]() $\{{\alpha <\kappa }~\vert ~{{\mathrm {{cof}}(\alpha )}=\omega }\}$
to
$\{{\alpha <\kappa }~\vert ~{{\mathrm {{cof}}(\alpha )}=\omega }\}$
to
![]() $\mathrm {{HOD}}$
identifies with the intersection of a small number of ordinal definable normal measures on
$\mathrm {{HOD}}$
identifies with the intersection of a small number of ordinal definable normal measures on
![]() $\kappa $
in
$\kappa $
in
![]() $\mathrm {{HOD}}$
(see [Reference Ben-Neria and Hayut2, Lemma 2.4]). Since, in
$\mathrm {{HOD}}$
(see [Reference Ben-Neria and Hayut2, Lemma 2.4]). Since, in
![]() $\mathrm {{HOD}}$
, many of the sets in this intersection do not contain a closed unbounded subset, it follows that there are many subsets of the cardinal
$\mathrm {{HOD}}$
, many of the sets in this intersection do not contain a closed unbounded subset, it follows that there are many subsets of the cardinal
![]() $\kappa $
that are
$\kappa $
that are
![]() $\mathrm {{HOD}}$
-stationary (i.e., that meet every closed unbounded subset of
$\mathrm {{HOD}}$
-stationary (i.e., that meet every closed unbounded subset of
![]() $\kappa $
that is an element of
$\kappa $
that is an element of
![]() $\mathrm {{HOD}}$
) but are not stationary subsets of
$\mathrm {{HOD}}$
) but are not stationary subsets of
![]() $\kappa $
in V.
$\kappa $
in V.
Motivated by this observation, the purpose of the work presented in this paper is to study the extent to which hierarchies of definable closed unbounded subsets of an uncountable cardinal
![]() $\kappa $
can approximate the full closed unbounded filter on
$\kappa $
can approximate the full closed unbounded filter on
![]() $\kappa $
, where the different hierarchies are given in terms of the complexity of the defining formulas (e.g.,
$\kappa $
, where the different hierarchies are given in terms of the complexity of the defining formulas (e.g.,
![]() $\Sigma _n$
-formulasFootnote
1
for some natural number n) and the set of parameters allowed in these formulas (e.g., ordinal parameters or parameters contained in
$\Sigma _n$
-formulasFootnote
1
for some natural number n) and the set of parameters allowed in these formulas (e.g., ordinal parameters or parameters contained in
![]() $\mathrm {H}_{\kappa }$
). Since ordinal definable sets of ordinals can be represented as the unique solutions of
$\mathrm {H}_{\kappa }$
). Since ordinal definable sets of ordinals can be represented as the unique solutions of
![]() $\Sigma _2$
-formulas with ordinal parameters (see the proof of [Reference Jech9, Lemma 13.25] for details) and closed unbounded subsets of uncountable cardinals
$\Sigma _2$
-formulas with ordinal parameters (see the proof of [Reference Jech9, Lemma 13.25] for details) and closed unbounded subsets of uncountable cardinals
![]() $\kappa $
that are definable by
$\kappa $
that are definable by
![]() $\Sigma _0$
-formulas with ordinals and elements of
$\Sigma _0$
-formulas with ordinals and elements of
![]() $\mathrm {H}_{\kappa }$
can be shown to have a very simple, eventually periodic structure,Footnote
2
the first place to expect different phenomena is with
$\mathrm {H}_{\kappa }$
can be shown to have a very simple, eventually periodic structure,Footnote
2
the first place to expect different phenomena is with
![]() $\Sigma _1$
-definable closed unbounded sets. In order to motivate the definitions and results contained in this paper, we start by presenting two settings in which
$\Sigma _1$
-definable closed unbounded sets. In order to motivate the definitions and results contained in this paper, we start by presenting two settings in which
![]() $\Sigma _1$
-definable closed unbounded sets give an optimal approximation to the collection of all closed unbounded sets:
$\Sigma _1$
-definable closed unbounded sets give an optimal approximation to the collection of all closed unbounded sets:
-
• In Gödel’s constructible universe L, every subset (and, in particular, every closed unbounded subset) of an infinite cardinal
 $\kappa $
is the unique solution of a
$\kappa $
is the unique solution of a
 $\Sigma _1$
-formula with parameters from
$\Sigma _1$
-formula with parameters from
 $\kappa ^+$
. This follows directly from the fact that every such subset is the
$\kappa ^+$
. This follows directly from the fact that every such subset is the
 $\eta $
-th element in the canonical well-ordering of L for some
$\eta $
-th element in the canonical well-ordering of L for some
 $\eta <\kappa ^+$
, and transitive models of
$\eta <\kappa ^+$
, and transitive models of
 ${\text {"}\hspace {0.3ex}{\mathrm {{ZFC}}^-+{V=L}}\hspace {0.3ex}\text {"}}$
containing an ordinal
${\text {"}\hspace {0.3ex}{\mathrm {{ZFC}}^-+{V=L}}\hspace {0.3ex}\text {"}}$
containing an ordinal
 $\eta $
can uniformly compute the initial segment of order-type
$\eta $
can uniformly compute the initial segment of order-type
 $\eta +1$
of this well-ordering.
$\eta +1$
of this well-ordering. -
• Martin’s Maximum
 $\mathrm {{M}}\mathrm {{M}}$
implies that every closed unbounded subset of
$\mathrm {{M}}\mathrm {{M}}$
implies that every closed unbounded subset of
 $\omega _1$
contains a closed unbounded subset that is the unique solution of a
$\omega _1$
contains a closed unbounded subset that is the unique solution of a
 $\Sigma _1$
-formula that only uses the ordinal
$\Sigma _1$
-formula that only uses the ordinal
 $\omega _1$
and real numbers as parameters. This statement follows directly from results of Woodin that show that
$\omega _1$
and real numbers as parameters. This statement follows directly from results of Woodin that show that
 $\mathrm {{M}}\mathrm {{M}}$
implies admissible club guessing (see [Reference H. Woodin20, Theorems 3.16, 3.17 & 3.19]).
$\mathrm {{M}}\mathrm {{M}}$
implies admissible club guessing (see [Reference H. Woodin20, Theorems 3.16, 3.17 & 3.19]).
In addition, results that will be contained in a sequel to this paper show that for every uncountable cardinal
![]() $\kappa $
satisfying
$\kappa $
satisfying
![]() $\kappa ^{{<}\kappa }=\kappa $
, there is cofinality-preserving forcing extension
$\kappa ^{{<}\kappa }=\kappa $
, there is cofinality-preserving forcing extension
![]() $V[G]$
of the ground model V in which there exists a subset E of
$V[G]$
of the ground model V in which there exists a subset E of
![]() $\kappa $
such that every closed unbounded subset of
$\kappa $
such that every closed unbounded subset of
![]() $\kappa $
contains a closed unbounded subset that is the unique solution of a
$\kappa $
contains a closed unbounded subset that is the unique solution of a
![]() $\Sigma _1$
-formula that only uses the set E and ordinals less than
$\Sigma _1$
-formula that only uses the set E and ordinals less than
![]() $\kappa ^+$
as parameters.
$\kappa ^+$
as parameters.
In contrast to these settings, the results of this paper will isolate several canonical contexts in which collections of
![]() $\Sigma _1$
-definable closed unbounded sets fail to approximate the closed unbounded filter. In order to formulate these results, we now specify the notions of definability used in this paper.
$\Sigma _1$
-definable closed unbounded sets fail to approximate the closed unbounded filter. In order to formulate these results, we now specify the notions of definability used in this paper.
Definition 1.1 A class
![]() $\Gamma $
is definable by a formula
$\Gamma $
is definable by a formula
![]() $\varphi (v_0,\ldots ,v_n)$
and parameters
$\varphi (v_0,\ldots ,v_n)$
and parameters
![]() $y_0,\ldots ,y_{n-1}$
if
$y_0,\ldots ,y_{n-1}$
if
Throughout this paper, we study the definability of certain sets of ordinals. Given such a set E, we will mostly consider the questions that ask whether the set
![]() $\{E\}$
is definable (in the sense of Definition 1.1) by certain formulas with parameters coming from a given class. Note that this form of definability differs from the statement that the set E itself is definable (again in the sense of Definition 1.1) in the given way. While the former implies the latter, it is easy to see that the converse implication fails for the set
$\{E\}$
is definable (in the sense of Definition 1.1) by certain formulas with parameters coming from a given class. Note that this form of definability differs from the statement that the set E itself is definable (again in the sense of Definition 1.1) in the given way. While the former implies the latter, it is easy to see that the converse implication fails for the set
![]() $\omega _1$
of all countable ordinals and definability by
$\omega _1$
of all countable ordinals and definability by
![]() $\Sigma _1$
-formulas without parameters.
$\Sigma _1$
-formulas without parameters.
We now introduce the main concepts studied in this paper:
Definition 1.2 Let n be a natural number, let
![]() $\kappa $
be a uncountable cardinal, and let S be a subset of
$\kappa $
be a uncountable cardinal, and let S be a subset of
![]() $\kappa $
.
$\kappa $
.
-
(1) Given a class R, the subset S is
 $\Sigma _n(R)$
-stationary in
$\Sigma _n(R)$
-stationary in
 $\kappa $
if
$\kappa $
if
 $C\cap S\neq \emptyset $
holds for every closed unbounded subset C of
$C\cap S\neq \emptyset $
holds for every closed unbounded subset C of
 $\kappa $
with the property that the set
$\kappa $
with the property that the set
 $\{C\}$
is definable by a
$\{C\}$
is definable by a
 $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
 $R\cup \{\kappa \}$
.
$R\cup \{\kappa \}$
. -
(2) The subset S is
 $\Sigma _n$
-stationary in
$\Sigma _n$
-stationary in
 $\kappa $
if it is
$\kappa $
if it is
 $\Sigma _n(\emptyset )$
-stationary in
$\Sigma _n(\emptyset )$
-stationary in
 $\kappa $
.
$\kappa $
. -
(3) Given a class R, the subset S is
 $\boldsymbol {\Sigma }_n(R)$
-stationary in
$\boldsymbol {\Sigma }_n(R)$
-stationary in
 $\kappa $
if it is
$\kappa $
if it is
 $\Sigma _n(R\cup \mathrm {H}_{\kappa })$
-stationary in
$\Sigma _n(R\cup \mathrm {H}_{\kappa })$
-stationary in
 $\kappa $
.
$\kappa $
. -
(4) The subset S is
 $\boldsymbol {\Sigma }_n$
-stationary in
$\boldsymbol {\Sigma }_n$
-stationary in
 $\kappa $
if it is
$\kappa $
if it is
 $\boldsymbol {\Sigma }_n(\emptyset )$
-stationary in
$\boldsymbol {\Sigma }_n(\emptyset )$
-stationary in
 $\kappa $
.
$\kappa $
.
Trivially, all stationary subsets of a given uncountable cardinal
![]() $\kappa $
are
$\kappa $
are
![]() $\Sigma _n(R)$
-stationary in
$\Sigma _n(R)$
-stationary in
![]() $\kappa $
for every parameter class R and every natural number n. As indicated by Definition 1.2, our focus in this paper will be on natural classes R such as
$\kappa $
for every parameter class R and every natural number n. As indicated by Definition 1.2, our focus in this paper will be on natural classes R such as
![]() $\mathrm {{Ord}}$
,
$\mathrm {{Ord}}$
,
![]() $\mathrm {H}_{\kappa }$
,
$\mathrm {H}_{\kappa }$
,
![]() $\mathrm {H}_{\mu }$
for some
$\mathrm {H}_{\mu }$
for some
![]() $\mu < \kappa $
, and their combinations. We therefore view the existence of nonstationary
$\mu < \kappa $
, and their combinations. We therefore view the existence of nonstationary
![]() $\Sigma _n(R)$
-stationary sets as a measure for the discrepancy between the collection of
$\Sigma _n(R)$
-stationary sets as a measure for the discrepancy between the collection of
![]() $\Sigma _n(R)$
-definable closed unbounded subsets and the collection of all closed unbounded subsets. Our results will isolate several settings in which highly nonstationary sets (such as singletons, or sets of successor cardinals below a limit cardinal) are stationary for rich collections of definable sets. In particular, even in the case of singular cardinals of countable cofinality, where stationarity coincides with coboundedness, we will present canonical examples of such cardinals in which sparse subsets are
$\Sigma _n(R)$
-definable closed unbounded subsets and the collection of all closed unbounded subsets. Our results will isolate several settings in which highly nonstationary sets (such as singletons, or sets of successor cardinals below a limit cardinal) are stationary for rich collections of definable sets. In particular, even in the case of singular cardinals of countable cofinality, where stationarity coincides with coboundedness, we will present canonical examples of such cardinals in which sparse subsets are
![]() $\Sigma _n(R)$
-stationary. The proofs of all these results reveal that, in the given settings, the considered collections of
$\Sigma _n(R)$
-stationary. The proofs of all these results reveal that, in the given settings, the considered collections of
![]() $\Sigma _n(R)$
-definable closed unbounded subsets and
$\Sigma _n(R)$
-definable closed unbounded subsets and
![]() $\Sigma _n(R)$
-stationary sets possess many of the structural features provable for the collections of closed unbounded and stationary subsets of regular uncountable cardinals. Below, we list six of our main results that best illustrate the phenomenon described above:
$\Sigma _n(R)$
-stationary sets possess many of the structural features provable for the collections of closed unbounded and stationary subsets of regular uncountable cardinals. Below, we list six of our main results that best illustrate the phenomenon described above:
-
• If
 $\kappa $
is a Ramsey cardinal, then every unbounded subset of
$\kappa $
is a Ramsey cardinal, then every unbounded subset of
 $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
 $\boldsymbol {\Sigma }_1$
-stationary (Theorem 4.1).
$\boldsymbol {\Sigma }_1$
-stationary (Theorem 4.1). -
• If
 $\kappa $
is a (possibly singular) limit of measurable cardinals, then every unbounded subset of
$\kappa $
is a (possibly singular) limit of measurable cardinals, then every unbounded subset of
 $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary (Theorem 4.6).
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary (Theorem 4.6). -
• If
 $\omega _\omega $
is a Jónsson cardinal, then every unbounded subset of
$\omega _\omega $
is a Jónsson cardinal, then every unbounded subset of
 $\{{\omega _n}~\vert ~{n<\omega }\}$
is
$\{{\omega _n}~\vert ~{n<\omega }\}$
is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\omega _\omega $
(Theorem 4.13).
$\omega _\omega $
(Theorem 4.13). -
• It is equiconsistent with the existence of a measurable cardinal that every unbounded subset of
 $\{{\omega _n}~\vert ~{n<\omega }\}$
is
$\{{\omega _n}~\vert ~{n<\omega }\}$
is
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
 $\omega _\omega $
(Theorem 5.3).
$\omega _\omega $
(Theorem 5.3). -
• It is equiconsistent with the existence of a Mahlo cardinal that there is a regular cardinal
 $\mu $
for which the singleton
$\mu $
for which the singleton
 $\{\mu \}$
is
$\{\mu \}$
is
 $\Sigma _1(\mathrm {H}_{\mu })$
-stationary in
$\Sigma _1(\mathrm {H}_{\mu })$
-stationary in
 $\mu ^+$
(Theorem 5.11).
$\mu ^+$
(Theorem 5.11). -
• While it is provable that for every set A of cardinality less than the reaping number
 $\mathfrak {r}$
Footnote
3
and every singular cardinal
$\mathfrak {r}$
Footnote
3
and every singular cardinal
 $\kappa $
of countable cofinality, there are disjoint
$\kappa $
of countable cofinality, there are disjoint
 $\Sigma _1(A)$
-stationary subsets of
$\Sigma _1(A)$
-stationary subsets of
 $\kappa $
(Proposition 2.8), it is equiconsistent with the existence of a measurable cardinal that there is a singular cardinal
$\kappa $
(Proposition 2.8), it is equiconsistent with the existence of a measurable cardinal that there is a singular cardinal
 $\kappa $
of countable cofinality such that for every subset A of
$\kappa $
of countable cofinality such that for every subset A of
 $\mathrm {H}_{\kappa }$
of cardinality
$\mathrm {H}_{\kappa }$
of cardinality
 $\mathfrak {r}$
, there are are disjoint
$\mathfrak {r}$
, there are are disjoint
 $\Sigma _1(A)$
-stationary subsets of
$\Sigma _1(A)$
-stationary subsets of
 $\kappa $
(Corollary 5.10).
$\kappa $
(Corollary 5.10).
We now briefly outline the structure of this paper: In Section 2, we prove preliminary results about the theory of
![]() $\Sigma _n(R)$
-stationary sets using mostly combinatorial arguments. In addition, we introduce an auxiliary property of
$\Sigma _n(R)$
-stationary sets using mostly combinatorial arguments. In addition, we introduce an auxiliary property of
![]() $\Sigma _n$
-undefinability of an ordinal, which plays a key role in the result of the paper. In Section 3, we examine
$\Sigma _n$
-undefinability of an ordinal, which plays a key role in the result of the paper. In Section 3, we examine
![]() $\Sigma _1$
-definability in the Dodd-Jensen core model and prove several results regarding
$\Sigma _1$
-definability in the Dodd-Jensen core model and prove several results regarding
![]() $\Sigma _1$
-stationary sets in
$\Sigma _1$
-stationary sets in
![]() $\mathrm {{K}}^{DJ}$
. Section 4 is devoted to showing that
$\mathrm {{K}}^{DJ}$
. Section 4 is devoted to showing that
![]() $\Sigma _1$
-stationarity is weak in the presence of sufficiently large cardinals (e.g., measurable cardinals or stably measurable cardinals) or at small cardinals with strong partition properties (e.g., when
$\Sigma _1$
-stationarity is weak in the presence of sufficiently large cardinals (e.g., measurable cardinals or stably measurable cardinals) or at small cardinals with strong partition properties (e.g., when
![]() $\omega _\omega $
is Jónsson). In Section 5, we build on the results about
$\omega _\omega $
is Jónsson). In Section 5, we build on the results about
![]() $\mathrm {{K}}^{DJ}$
as well as on forcing results with large cardinals to prove several equiconsistency results about weakness of
$\mathrm {{K}}^{DJ}$
as well as on forcing results with large cardinals to prove several equiconsistency results about weakness of
![]() $\Sigma _1(\mathrm{Ord})$
-definable closed unbounded sets. In Section 6, we conclude the paper by listing some problems left open by our results.
$\Sigma _1(\mathrm{Ord})$
-definable closed unbounded sets. In Section 6, we conclude the paper by listing some problems left open by our results.
2 Preliminaries about
 $\Sigma _n$
-Stationary sets
$\Sigma _n$
-Stationary sets
In this section, we start to develop the theory of
![]() $\Sigma _n(R)$
-stationary sets for natural classes R.
$\Sigma _n(R)$
-stationary sets for natural classes R.
2.1 A proper hierarchy
In order to motivate the below results, we start our investigations of
![]() $\Sigma _n(R)$
-stationary sets by presenting a setting in which these sets form a properly descending hierarchy in the parameter n.
$\Sigma _n(R)$
-stationary sets by presenting a setting in which these sets form a properly descending hierarchy in the parameter n.
Theorem 2.1 Assume that the
![]() $\mathrm {{GCH}}$
holds. Then, for every uncountable regular cardinal
$\mathrm {{GCH}}$
holds. Then, for every uncountable regular cardinal
![]() $\kappa $
and every cardinal
$\kappa $
and every cardinal
![]() $\theta $
satisfying
$\theta $
satisfying
![]() $\theta =\theta ^\kappa $
, there is a uniformly definable partial order
$\theta =\theta ^\kappa $
, there is a uniformly definable partial order
![]() $\mathbb {P}_{\kappa ,\theta }$
such that forcing with
$\mathbb {P}_{\kappa ,\theta }$
such that forcing with
![]() $\mathbb {P}_{\kappa ,\theta }$
preserves cofinalities, and if G is
$\mathbb {P}_{\kappa ,\theta }$
preserves cofinalities, and if G is
![]() $\mathbb {P}_{\kappa ,\theta }$
-generic over V, then, in
$\mathbb {P}_{\kappa ,\theta }$
-generic over V, then, in
![]() $V[G]$
, for every natural number
$V[G]$
, for every natural number
![]() $n>0$
and every set A of cardinality less than
$n>0$
and every set A of cardinality less than
![]() $\theta $
with the property that the set
$\theta $
with the property that the set
![]() $\{A\}$
is definable by a
$\{A\}$
is definable by a
![]() $\Sigma _2$
-formula with parameters in A, there is a subset of
$\Sigma _2$
-formula with parameters in A, there is a subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
and not
$\kappa $
and not
![]() $\Sigma _{n+1}(A)$
-stationary in
$\Sigma _{n+1}(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
Note that the definability assumptions on the parameter set A stated in the above theorem are satisfied in the case where
![]() $\theta =\kappa ^{++}$
and
$\theta =\kappa ^{++}$
and
![]() $A=\mathrm {H}_{\kappa }\cup \kappa ^+$
. We therefore directly get the following corollary whose statement should be compared with the two settings discussed in Section 1, in which all
$A=\mathrm {H}_{\kappa }\cup \kappa ^+$
. We therefore directly get the following corollary whose statement should be compared with the two settings discussed in Section 1, in which all
![]() $\boldsymbol {\Sigma }_1(\kappa ^+)$
-stationary subsets of an uncountable cardinal
$\boldsymbol {\Sigma }_1(\kappa ^+)$
-stationary subsets of an uncountable cardinal
![]() $\kappa $
are stationary.
$\kappa $
are stationary.
Corollary 2.2 If the
![]() $\mathrm {{GCH}}$
holds, then for every uncountable regular cardinal
$\mathrm {{GCH}}$
holds, then for every uncountable regular cardinal
![]() $\kappa $
, there is a uniformly definable cofinality preserving partial order
$\kappa $
, there is a uniformly definable cofinality preserving partial order
![]() $\mathbb {P}_\kappa $
with the property that whenever G is
$\mathbb {P}_\kappa $
with the property that whenever G is
![]() $\mathbb {P}_\kappa $
-generic over V and
$\mathbb {P}_\kappa $
-generic over V and
![]() $n>0$
is a natural number, then, in
$n>0$
is a natural number, then, in
![]() $V[G]$
, there is a subset of
$V[G]$
, there is a subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\boldsymbol {\Sigma }_n(\kappa ^+)$
-stationary in
$\boldsymbol {\Sigma }_n(\kappa ^+)$
-stationary in
![]() $\kappa $
and not
$\kappa $
and not
![]() $\boldsymbol {\Sigma }_{n+1}(\kappa ^+)$
-stationary in
$\boldsymbol {\Sigma }_{n+1}(\kappa ^+)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
The above result is a consequence of the following two observations that might be of independent interest:
Proposition 2.3 Let
![]() $n>0$
be a natural number, let
$n>0$
be a natural number, let
![]() $\kappa $
be an uncountable cardinal with
$\kappa $
be an uncountable cardinal with
![]() ${\mathcal {P}}({\kappa })\subseteq \mathrm {{HOD}}$
, and let A be a set with the property that the set
${\mathcal {P}}({\kappa })\subseteq \mathrm {{HOD}}$
, and let A be a set with the property that the set
![]() $\{A\}$
is definable by a
$\{A\}$
is definable by a
![]() $\Sigma _{n+1}$
-formula with parameters in A. If there is a nonstationary subset of
$\Sigma _{n+1}$
-formula with parameters in A. If there is a nonstationary subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
, then there is a subset of
$\kappa $
, then there is a subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
and not
$\kappa $
and not
![]() $\Sigma _{n+1}(A)$
-stationary in
$\Sigma _{n+1}(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
Proof Let E be the least nonstationary subset of
![]() $\kappa $
in the canonical well-ordering of
$\kappa $
in the canonical well-ordering of
![]() $\mathrm {{HOD}}$
that is
$\mathrm {{HOD}}$
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
. Since the collection of all initial segments of the canonical well-ordering of
$\kappa $
. Since the collection of all initial segments of the canonical well-ordering of
![]() $\mathrm {{HOD}}$
is definable by a
$\mathrm {{HOD}}$
is definable by a
![]() $\Sigma _2$
-formula without parameters, and the collection
$\Sigma _2$
-formula without parameters, and the collection
![]() $C^{(n)}$
of all ordinals
$C^{(n)}$
of all ordinals
![]() $\lambda $
with
$\lambda $
with
![]() $V_\lambda \prec _{\Sigma _n}V$
is definable by a
$V_\lambda \prec _{\Sigma _n}V$
is definable by a
![]() $\Pi _n$
-formula without parameters (see [Reference Bagaria1, Section 1]), we know that the set
$\Pi _n$
-formula without parameters (see [Reference Bagaria1, Section 1]), we know that the set
![]() $\{E\}$
is definable by a
$\{E\}$
is definable by a
![]() $\Sigma _{n+1}$
-formula with parameters in A. Let C denote the least closed unbounded subset of
$\Sigma _{n+1}$
-formula with parameters in A. Let C denote the least closed unbounded subset of
![]() $\kappa $
in the canonical well-ordering of
$\kappa $
in the canonical well-ordering of
![]() $\mathrm {{HOD}}$
that is disjoint from E. But then we know that the set
$\mathrm {{HOD}}$
that is disjoint from E. But then we know that the set
![]() $\{C\}$
is also definable by a
$\{C\}$
is also definable by a
![]() $\Sigma _{n+1}$
-formula with parameters in A, and therefore, C witnesses that E is not
$\Sigma _{n+1}$
-formula with parameters in A, and therefore, C witnesses that E is not
![]() $\Sigma _{n+1}(A)$
-stationary in
$\Sigma _{n+1}(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
Proposition 2.4 Let
![]() $\kappa $
be an uncountable cardinal with
$\kappa $
be an uncountable cardinal with
![]() $\kappa ^{{<}\kappa }=\kappa $
, let
$\kappa ^{{<}\kappa }=\kappa $
, let
![]() $\theta>\kappa $
be a cardinal with
$\theta>\kappa $
be a cardinal with
![]() $\theta ^\kappa =\theta $
, let G be
$\theta ^\kappa =\theta $
, let G be
![]() $\mathrm {{Add}}({\kappa },{\theta })$
-generic over
$\mathrm {{Add}}({\kappa },{\theta })$
-generic over
![]() $\mathrm {{V}}$
, and let
$\mathrm {{V}}$
, and let
![]() $\mathcal {C}$
be a collection of closed unbounded subsets of
$\mathcal {C}$
be a collection of closed unbounded subsets of
![]() $\kappa $
of cardinality less than
$\kappa $
of cardinality less than
![]() $\theta $
in
$\theta $
in
![]() $V[G]$
. Then, in
$V[G]$
. Then, in
![]() $\mathrm {{V}}[G]$
, there exists a nonstationary subset E of
$\mathrm {{V}}[G]$
, there exists a nonstationary subset E of
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $C\cap E\neq \emptyset $
holds for all
$C\cap E\neq \emptyset $
holds for all
![]() $C\in \mathcal {C}$
.
$C\in \mathcal {C}$
.
Proof By our assumptions, we can find a generic extension M of
![]() $\mathrm {{V}}$
such that
$\mathrm {{V}}$
such that
![]() $\mathcal {C}\in M\subsetneq \mathrm {{V}}[G]$
and
$\mathcal {C}\in M\subsetneq \mathrm {{V}}[G]$
and
![]() $\mathrm {{V}}[G]$
is a nontrivial
$\mathrm {{V}}[G]$
is a nontrivial
![]() $\mathrm {{Add}}({\kappa },{\theta })$
-generic extension of M. Let
$\mathrm {{Add}}({\kappa },{\theta })$
-generic extension of M. Let
![]() $H\in \mathrm {{V}}[G]$
be
$H\in \mathrm {{V}}[G]$
be
![]() $\mathrm {{Add}}({\kappa },{1})$
-generic over M, let X denote the subset of
$\mathrm {{Add}}({\kappa },{1})$
-generic over M, let X denote the subset of
![]() $\kappa $
corresponding to H, and set
$\kappa $
corresponding to H, and set
![]() $E=X\setminus \mathrm {{Lim}}(X)$
. Genericity then ensures that E intersects every unbounded subset of
$E=X\setminus \mathrm {{Lim}}(X)$
. Genericity then ensures that E intersects every unbounded subset of
![]() $\kappa $
in M. In particular, we know that
$\kappa $
in M. In particular, we know that
![]() $C\cap E\neq \emptyset $
holds for every
$C\cap E\neq \emptyset $
holds for every
![]() $C\in \mathcal {C}$
. Finally, since E is disjoint from
$C\in \mathcal {C}$
. Finally, since E is disjoint from
![]() $\mathrm {{Lim}}(X)$
, we know that E is a nonstationary subset of
$\mathrm {{Lim}}(X)$
, we know that E is a nonstationary subset of
![]() $\kappa $
in
$\kappa $
in
![]() $\mathrm {{V}}[G]$
.
$\mathrm {{V}}[G]$
.
A combination of these two observations now directly yields the desired consistency proof:
Proof of Theorem 2.1
Assume that the
![]() $\mathrm {{GCH}}$
holds. Given an uncountable regular cardinal
$\mathrm {{GCH}}$
holds. Given an uncountable regular cardinal
![]() $\kappa $
and a cardinal
$\kappa $
and a cardinal
![]() $\theta $
satisfying
$\theta $
satisfying
![]() $\theta =\theta ^\kappa $
, we define
$\theta =\theta ^\kappa $
, we define
![]() $\mathbb {P}_{\kappa ,\theta }$
to be the two-step iteration
$\mathbb {P}_{\kappa ,\theta }$
to be the two-step iteration
![]() $\mathrm {{Add}}({\kappa },{\theta })*\dot {{\mathbb {Q}}}$
, where
$\mathrm {{Add}}({\kappa },{\theta })*\dot {{\mathbb {Q}}}$
, where
![]() $\dot {{\mathbb {Q}}}$
is the canonical
$\dot {{\mathbb {Q}}}$
is the canonical
![]() $\mathrm {{Add}}({\kappa },{\theta })$
-name for the
$\mathrm {{Add}}({\kappa },{\theta })$
-name for the
![]() ${<}\theta ^+$
-closed partial order that codes
${<}\theta ^+$
-closed partial order that codes
![]() ${\mathcal {P}}({\kappa })$
into the
${\mathcal {P}}({\kappa })$
into the
![]() $\mathrm {{GCH}}$
-pattern above
$\mathrm {{GCH}}$
-pattern above
![]() $\theta ^+$
(see, for example, [Reference Fuchs, Hamkins and Reitz7]). Let
$\theta ^+$
(see, for example, [Reference Fuchs, Hamkins and Reitz7]). Let
![]() $G*H$
be (
$G*H$
be (
![]() $\mathrm {{Add}}({\kappa },{\theta })*\dot {{\mathbb {Q}}}$
)-generic over V. Fix a natural number
$\mathrm {{Add}}({\kappa },{\theta })*\dot {{\mathbb {Q}}}$
)-generic over V. Fix a natural number
![]() $n>0$
and a set
$n>0$
and a set
![]() $A\in V[G,H]$
of cardinality less than
$A\in V[G,H]$
of cardinality less than
![]() $\theta $
with the property that, in
$\theta $
with the property that, in
![]() $V[G,H]$
, the set
$V[G,H]$
, the set
![]() $\{A\}$
is definable by a
$\{A\}$
is definable by a
![]() $\Sigma _2$
-formula with parameters in A. Since
$\Sigma _2$
-formula with parameters in A. Since
![]() ${\mathcal {P}}({{\mathcal {P}}({\kappa })})^{V[G]}={\mathcal {P}}({{\mathcal {P}}({\kappa })})^{V[G,H]}$
and, in
${\mathcal {P}}({{\mathcal {P}}({\kappa })})^{V[G]}={\mathcal {P}}({{\mathcal {P}}({\kappa })})^{V[G,H]}$
and, in
![]() $V[G,H]$
, there are less than
$V[G,H]$
, there are less than
![]() $\theta $
-many closed unbounded subsets C of
$\theta $
-many closed unbounded subsets C of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
, an application of Proposition 2.4 shows that, in
$A\cup \{\kappa \}$
, an application of Proposition 2.4 shows that, in
![]() $V[G,H]$
, there is a nonstationary subset of
$V[G,H]$
, there is a nonstationary subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
. But our setup ensures that
$\kappa $
. But our setup ensures that
![]() ${\mathcal {P}}({\kappa })^{V[G]}={\mathcal {P}}({\kappa })^{V[G,H]}\subseteq \mathrm {{HOD}}^{V[G,H]}$
, and hence, Proposition 2.3 allows us to conclude that, in
${\mathcal {P}}({\kappa })^{V[G]}={\mathcal {P}}({\kappa })^{V[G,H]}\subseteq \mathrm {{HOD}}^{V[G,H]}$
, and hence, Proposition 2.3 allows us to conclude that, in
![]() $V[G,H]$
, there is a subset of
$V[G,H]$
, there is a subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
and not
$\kappa $
and not
![]() $\Sigma _{n+1}(A)$
-stationary in
$\Sigma _{n+1}(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
In a sequel to this paper, we will provide analogous results about the properness of the hierarchy of
![]() $\Sigma _n(A)$
-stationary sets for singular cardinals.
$\Sigma _n(A)$
-stationary sets for singular cardinals.
2.2 Combinatorial arguments
We now continue by analyzing basic structural features of the collection of all
![]() $\Sigma _n(A)$
-stationary sets. All results presented in this section are purely combinatorial in the sense that they only rely on counting arguments. We nevertheless decided to phrase them in such a way that they make statements about collections of definable subsets. These formulations motivate several of our later results that will show that, in general, we cannot relax the stated assumptions on the sizes of parameter sets. We start our analysis by comparing
$\Sigma _n(A)$
-stationary sets. All results presented in this section are purely combinatorial in the sense that they only rely on counting arguments. We nevertheless decided to phrase them in such a way that they make statements about collections of definable subsets. These formulations motivate several of our later results that will show that, in general, we cannot relax the stated assumptions on the sizes of parameter sets. We start our analysis by comparing
![]() $\Sigma _n(A)$
-stationarity with standard stationarity and isolating settings in which counting arguments ensure the existence of
$\Sigma _n(A)$
-stationarity with standard stationarity and isolating settings in which counting arguments ensure the existence of
![]() $\Sigma _n(A)$
-stationary sets that are not stationary.
$\Sigma _n(A)$
-stationary sets that are not stationary.
Proposition 2.5 If
![]() $\kappa $
is a cardinal of uncountable cofinality, A is a set of cardinality at most
$\kappa $
is a cardinal of uncountable cofinality, A is a set of cardinality at most
![]() ${\mathrm {{cof}}(\kappa )}$
, and n is a natural number, then there is an unbounded, nonstationary subset of
${\mathrm {{cof}}(\kappa )}$
, and n is a natural number, then there is an unbounded, nonstationary subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
Proof Let
![]() $\langle {C_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
be an enumeration of all closed unbounded subsets C of
$\langle {C_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
be an enumeration of all closed unbounded subsets C of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
. In addition, define C to be a diagonal intersection of these sets with respect to some strictly increasing continuous sequence of order type
$A\cup \{\kappa \}$
. In addition, define C to be a diagonal intersection of these sets with respect to some strictly increasing continuous sequence of order type
![]() ${\mathrm {{cof}}(\kappa )}$
in
${\mathrm {{cof}}(\kappa )}$
in
![]() $\kappa $
. Define
$\kappa $
. Define
![]() $S=C\setminus \mathrm {{Lim}}(C)$
. Then S is an unbounded and nonstationary subset of
$S=C\setminus \mathrm {{Lim}}(C)$
. Then S is an unbounded and nonstationary subset of
![]() $\kappa $
. Moreover, we have
$\kappa $
. Moreover, we have
![]() $C\cap S\neq \emptyset $
whenever C is a closed unbounded subset of
$C\cap S\neq \emptyset $
whenever C is a closed unbounded subset of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
.
$A\cup \{\kappa \}$
.
The results of this paper show that the implication in the above proposition can fail if we consider sets of parameters of cardinality
![]() ${\mathrm {{cof}}(\kappa )}^+$
. In the case of regular cardinals, the examples given in Section 1 about L and under
${\mathrm {{cof}}(\kappa )}^+$
. In the case of regular cardinals, the examples given in Section 1 about L and under
![]() $MM$
provide examples of such failures. For singular cardinals
$MM$
provide examples of such failures. For singular cardinals
![]() $\kappa $
of uncountable cofinality, Corollary 3.4 below will show that, in the Dodd-Jensen core model, stationarity coincides with
$\kappa $
of uncountable cofinality, Corollary 3.4 below will show that, in the Dodd-Jensen core model, stationarity coincides with
![]() $\Sigma _1({\mathcal {P}}({{\mathrm {{cof}}(\kappa )}}))$
-stationarity and therefore also with
$\Sigma _1({\mathcal {P}}({{\mathrm {{cof}}(\kappa )}}))$
-stationarity and therefore also with
![]() $\boldsymbol {\Sigma }_1$
-stationarity in
$\boldsymbol {\Sigma }_1$
-stationarity in
![]() $\kappa $
. Moreover, 5.2 shows that when
$\kappa $
. Moreover, 5.2 shows that when
![]() $\kappa $
is singular of uncountable cofinality, the existence of
$\kappa $
is singular of uncountable cofinality, the existence of
![]() $\boldsymbol {\Sigma }_1$
-stationarity subset of
$\boldsymbol {\Sigma }_1$
-stationarity subset of
![]() $\kappa $
that is not stationary is equiconsistent with the existence of
$\kappa $
that is not stationary is equiconsistent with the existence of
![]() ${\mathrm {{cof}}(\kappa )}$
many measurable cardinals. In the case of singular cardinals of countable cofinalities, Theorem 5.3 will give an analogous equiconsistency result. We start with a quick combinatorial argument.
${\mathrm {{cof}}(\kappa )}$
many measurable cardinals. In the case of singular cardinals of countable cofinalities, Theorem 5.3 will give an analogous equiconsistency result. We start with a quick combinatorial argument.
Proposition 2.6 If
![]() $\kappa $
is a singular cardinal of countable cofinality, A is a set of cardinality less than
$\kappa $
is a singular cardinal of countable cofinality, A is a set of cardinality less than
![]() $\kappa ^\omega $
, and n is a natural number, then there is an unbounded subset of
$\kappa ^\omega $
, and n is a natural number, then there is an unbounded subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
and whose complement in
$\kappa $
and whose complement in
![]() $\kappa $
is unbounded in
$\kappa $
is unbounded in
![]() $\kappa $
.
$\kappa $
.
Proof Since the set
![]() $[\kappa ]^\omega $
contains an almost disjoint family of cardinality
$[\kappa ]^\omega $
contains an almost disjoint family of cardinality
![]() $\kappa ^\omega $
that consists of unbounded subsets of
$\kappa ^\omega $
that consists of unbounded subsets of
![]() $\kappa $
, we can find an element
$\kappa $
, we can find an element
![]() $b\in [\kappa ]^\omega $
that is unbounded in
$b\in [\kappa ]^\omega $
that is unbounded in
![]() $\kappa $
and has the property that no infinite subset of b is definable by a
$\kappa $
and has the property that no infinite subset of b is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
. Then,
$A\cup \{\kappa \}$
. Then,
![]() $\kappa \setminus b$
is
$\kappa \setminus b$
is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
and the complement of this set in
$\kappa $
and the complement of this set in
![]() $\kappa $
is unbounded in
$\kappa $
is unbounded in
![]() $\kappa $
.
$\kappa $
.
We continue by comparing the structural properties of
![]() $\Sigma _n(A)$
-stationary sets with those of standard stationary sets. Our first focus in this comparison will be the question of the existence of disjoint
$\Sigma _n(A)$
-stationary sets with those of standard stationary sets. Our first focus in this comparison will be the question of the existence of disjoint
![]() $\Sigma _n(A)$
-stationary sets at various uncountable cardinals. In the case of cardinals of uncountable cofinality, the fact that all stationary sets are
$\Sigma _n(A)$
-stationary sets at various uncountable cardinals. In the case of cardinals of uncountable cofinality, the fact that all stationary sets are
![]() $\Sigma _n(A)$
-stationary already ensures the existence of such sets. The next result strengthens this conclusion by showing that a version of Solovay’s Theorem on the splitting of stationary sets holds for
$\Sigma _n(A)$
-stationary already ensures the existence of such sets. The next result strengthens this conclusion by showing that a version of Solovay’s Theorem on the splitting of stationary sets holds for
![]() $\Sigma _n(A)$
-stationary sets.
$\Sigma _n(A)$
-stationary sets.
Proposition 2.7 Suppose that
![]() $\kappa $
is a cardinal of uncountable cofinality, A is a set of cardinality
$\kappa $
is a cardinal of uncountable cofinality, A is a set of cardinality
![]() ${\mathrm {{cof}}(\kappa )}$
with
${\mathrm {{cof}}(\kappa )}$
with
![]() $A\cap \kappa $
cofinal in
$A\cap \kappa $
cofinal in
![]() $\kappa $
,
$\kappa $
,
![]() $n < \omega $
, and S is a
$n < \omega $
, and S is a
![]() $\Sigma _n(A)$
-stationary subset of
$\Sigma _n(A)$
-stationary subset of
![]() $\kappa $
. Then, there exists a partition
$\kappa $
. Then, there exists a partition
![]() $\langle {S_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
of S into
$\langle {S_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
of S into
![]() $\Sigma _n(A)$
-stationary subsets.
$\Sigma _n(A)$
-stationary subsets.
Proof Since
![]() $A\cap \kappa $
is unbounded in
$A\cap \kappa $
is unbounded in
![]() $\kappa $
, we know that there are
$\kappa $
, we know that there are
![]() ${\mathrm {{cof}}(\kappa )}$
-many
${\mathrm {{cof}}(\kappa )}$
-many
![]() $\Sigma _n(A)$
-definable closed unbounded subsets of
$\Sigma _n(A)$
-definable closed unbounded subsets of
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\langle {C_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
be an enumeration of all closed unbounded subsets C of
$\langle {C_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
be an enumeration of all closed unbounded subsets C of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
. Since the assumption that
$A\cup \{\kappa \}$
. Since the assumption that
![]() $A\cap \kappa $
is unbounded in
$A\cap \kappa $
is unbounded in
![]() $\kappa $
implies that
$\kappa $
implies that
![]() $C_\alpha \cap S$
is unbounded in
$C_\alpha \cap S$
is unbounded in
![]() $\kappa $
for all
$\kappa $
for all
![]() $\alpha <{\mathrm {{cof}}(\kappa )}$
, we can find a strictly increasing sequence
$\alpha <{\mathrm {{cof}}(\kappa )}$
, we can find a strictly increasing sequence
![]() $\langle {\sigma _\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
of elements of S with the property that
$\langle {\sigma _\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
of elements of S with the property that
![]() $\sigma _{{\prec }{\alpha _0},{\alpha _1}{\succ }}\in C_{\alpha _1}$
for all
$\sigma _{{\prec }{\alpha _0},{\alpha _1}{\succ }}\in C_{\alpha _1}$
for all
![]() $\alpha _0,\alpha _1<{\mathrm {{cof}}(\kappa )}$
, where
$\alpha _0,\alpha _1<{\mathrm {{cof}}(\kappa )}$
, where
![]() ${{\prec }{\cdot },{\cdot }{\succ }}:{\mathrm{Ord}\times \mathrm{Ord}}\longrightarrow {\mathrm{Ord}}$
denotes the Gödel pairing function. If we now pick a partition
${{\prec }{\cdot },{\cdot }{\succ }}:{\mathrm{Ord}\times \mathrm{Ord}}\longrightarrow {\mathrm{Ord}}$
denotes the Gödel pairing function. If we now pick a partition
![]() $\langle {S_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
of S with the property that
$\langle {S_\alpha }~\vert ~{\alpha <{\mathrm {{cof}}(\kappa )}}\rangle $
of S with the property that
![]() $\{{\sigma _{\alpha ,\beta }}~\vert ~{\beta <{\mathrm {{cof}}(\kappa )}}\}\subseteq S_\alpha $
holds for all
$\{{\sigma _{\alpha ,\beta }}~\vert ~{\beta <{\mathrm {{cof}}(\kappa )}}\}\subseteq S_\alpha $
holds for all
![]() $\alpha <{\mathrm {{cof}}(\kappa )}$
, then each
$\alpha <{\mathrm {{cof}}(\kappa )}$
, then each
![]() $S_\alpha $
is
$S_\alpha $
is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
In the case of cardinals of countable cofinality, the existence of disjoint
![]() $\Sigma _n(A)$
-stationary sets turns out to be closely connected to the reaping number
$\Sigma _n(A)$
-stationary sets turns out to be closely connected to the reaping number
![]() $\mathfrak {r}$
.
$\mathfrak {r}$
.
Definition 2.1
![]() $\mathfrak {r}$
is the least cardinality of a subset A of
$\mathfrak {r}$
is the least cardinality of a subset A of
![]() $[\omega ]^\omega $
with the property that for every
$[\omega ]^\omega $
with the property that for every
![]() $b\in [\omega ]^\omega $
, there is
$b\in [\omega ]^\omega $
, there is
![]() $a\in A$
such that either
$a\in A$
such that either
![]() $a\setminus b$
or
$a\setminus b$
or
![]() $a\cap b$
is finite.
$a\cap b$
is finite.
We will later show that, in general, the conclusion of the following proposition cannot be extended to sets of parameters of cardinality
![]() $\mathfrak {r}$
(see Corollaries 3.6 and 5.10 below).
$\mathfrak {r}$
(see Corollaries 3.6 and 5.10 below).
Proposition 2.8 Let
![]() $\kappa $
be a singular cardinal of countable cofinality, let A be a set of cardinality less than
$\kappa $
be a singular cardinal of countable cofinality, let A be a set of cardinality less than
![]() $\mathfrak {r}$
, and let n be a natural number. Then, there exists a subset E of
$\mathfrak {r}$
, and let n be a natural number. Then, there exists a subset E of
![]() $\kappa $
with the property that both E and
$\kappa $
with the property that both E and
![]() $\kappa \setminus E$
are
$\kappa \setminus E$
are
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
The proof of this proposition relies on the equivalence provided by the next lemma:
Lemma 2.9 The following statements are equivalent for every infinite cardinal
![]() $\theta $
:
$\theta $
:
-
(1)
 $\theta <\mathfrak {r}$
.
$\theta <\mathfrak {r}$
. -
(2) For every singular cardinal
 $\kappa $
of countable cofinality and every subset A of
$\kappa $
of countable cofinality and every subset A of
 $[\kappa ]^\omega $
that consists of cofinal subsets of
$[\kappa ]^\omega $
that consists of cofinal subsets of
 $\kappa $
and has cardinality at most
$\kappa $
and has cardinality at most
 $\theta $
, there exists a subset E of
$\theta $
, there exists a subset E of
 $\kappa $
such that for every
$\kappa $
such that for every
 $a\in A$
, both
$a\in A$
, both
 $a\cap E$
and
$a\cap E$
and
 $a\setminus E$
are infinite.
$a\setminus E$
are infinite. -
(3) There is a singular cardinal
 $\kappa $
of countable cofinality with the property that for every subset A of
$\kappa $
of countable cofinality with the property that for every subset A of
 $[\kappa ]^\omega $
that consists of cofinal subsets of
$[\kappa ]^\omega $
that consists of cofinal subsets of
 $\kappa $
and has cardinality at most
$\kappa $
and has cardinality at most
 $\theta $
, there exists a subset E of
$\theta $
, there exists a subset E of
 $\kappa $
such that for every
$\kappa $
such that for every
 $a\in A$
, both
$a\in A$
, both
 $a\cap E$
and
$a\cap E$
and
 $a\setminus E$
are infinite.
$a\setminus E$
are infinite.
Proof First, assume that (1) holds and (2) fails. Then, there is a singular cardinal
![]() $\kappa $
of countable cofinality and a subset A of
$\kappa $
of countable cofinality and a subset A of
![]() $[\kappa ]^\omega $
such that A consists of cofinal subsets of
$[\kappa ]^\omega $
such that A consists of cofinal subsets of
![]() $\kappa $
,
$\kappa $
,
![]() $\vert {A}\vert \leq \theta $
, and for every subset E of
$\vert {A}\vert \leq \theta $
, and for every subset E of
![]() $\kappa $
, there is
$\kappa $
, there is
![]() $a\in A$
such that either
$a\in A$
such that either
![]() $a\cap E$
or
$a\cap E$
or
![]() $a\setminus E$
is finite. Let
$a\setminus E$
is finite. Let
![]() $\langle {\kappa _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence that is cofinal in
$\langle {\kappa _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence that is cofinal in
![]() $\kappa $
with
$\kappa $
with
![]() $\kappa _0=0$
. Given
$\kappa _0=0$
. Given
![]() $a\in A$
, define
$a\in A$
, define
Since
![]() $\vert {A}\vert <\mathfrak {r}$
, we can now find
$\vert {A}\vert <\mathfrak {r}$
, we can now find
![]() $c\in [\omega ]^\omega $
with the property that for all
$c\in [\omega ]^\omega $
with the property that for all
![]() $a\in A$
, both
$a\in A$
, both
![]() $b_a\setminus c$
and
$b_a\setminus c$
and
![]() $b_a\cap c$
are infinite. Set
$b_a\cap c$
are infinite. Set
By our assumptions, there is
![]() $a\in A$
with the property that either
$a\in A$
with the property that either
![]() $a\setminus E$
or
$a\setminus E$
or
![]() $a\cap E$
is finite. But this implies that either
$a\cap E$
is finite. But this implies that either
![]() $b_a\setminus c$
or
$b_a\setminus c$
or
![]() $b_a\cap c$
is finite, a contradiction.
$b_a\cap c$
is finite, a contradiction.
Now, assume that (3) holds and (1) fails. Then, there is a singular cardinal
![]() $\kappa $
of countable cofinality with the property that for every subset A of
$\kappa $
of countable cofinality with the property that for every subset A of
![]() $[\kappa ]^\omega $
that consists of cofinal subsets of
$[\kappa ]^\omega $
that consists of cofinal subsets of
![]() $\kappa $
and has cardinality at most
$\kappa $
and has cardinality at most
![]() $\theta $
, there exists a subset E of
$\theta $
, there exists a subset E of
![]() $\kappa $
such that for every
$\kappa $
such that for every
![]() $a\in A$
, both
$a\in A$
, both
![]() $a\cap E$
and
$a\cap E$
and
![]() $a\setminus E$
are infinite. Fix
$a\setminus E$
are infinite. Fix
![]() $A\subseteq [\omega ]^\omega $
of cardinality
$A\subseteq [\omega ]^\omega $
of cardinality
![]() $\mathfrak {r}$
such that for every
$\mathfrak {r}$
such that for every
![]() $b\in [\omega ]^\omega $
, there exists
$b\in [\omega ]^\omega $
, there exists
![]() $a\in A$
with the property that either
$a\in A$
with the property that either
![]() $a\setminus b$
or
$a\setminus b$
or
![]() $a\cap b$
is finite. Pick a s strictly increasing sequence
$a\cap b$
is finite. Pick a s strictly increasing sequence
![]() $\langle {\kappa _n}~\vert ~{n<\omega }\rangle $
that is cofinal in
$\langle {\kappa _n}~\vert ~{n<\omega }\rangle $
that is cofinal in
![]() $\kappa $
and, given
$\kappa $
and, given
![]() $a\in A$
, define
$a\in A$
, define
![]() $b_a=\{{\kappa _n}~\vert ~{n\in a}\}\in [\kappa ]^\omega $
. Since
$b_a=\{{\kappa _n}~\vert ~{n\in a}\}\in [\kappa ]^\omega $
. Since
![]() $b_a$
is cofinal in
$b_a$
is cofinal in
![]() $\kappa $
for all
$\kappa $
for all
![]() $a\in A$
, we can now find a subset E of
$a\in A$
, we can now find a subset E of
![]() $\kappa $
such that for every
$\kappa $
such that for every
![]() $a\in A$
, both
$a\in A$
, both
![]() $b_a\cap E$
and
$b_a\cap E$
and
![]() $b_a\setminus E$
are infinite. Set
$b_a\setminus E$
are infinite. Set
![]() $c=\{{n<\omega }~\vert ~{\kappa _n\in E}\}\in [\omega ]^\omega $
. If
$c=\{{n<\omega }~\vert ~{\kappa _n\in E}\}\in [\omega ]^\omega $
. If
![]() $a\in A$
, then both
$a\in A$
, then both
![]() $a\setminus c$
and
$a\setminus c$
and
![]() $a\cap c$
are infinite, contradicting our assumptions on A.
$a\cap c$
are infinite, contradicting our assumptions on A.
Proof of Proposition 2.8
Let
![]() $\kappa $
be a singular cardinal of countable cofinality, let A be a set of cardinality less than
$\kappa $
be a singular cardinal of countable cofinality, let A be a set of cardinality less than
![]() $\mathfrak {r}$
, and let
$\mathfrak {r}$
, and let
![]() $n>0$
be a natural number. Then, there exists a subset
$n>0$
be a natural number. Then, there exists a subset
![]() $A'$
of
$A'$
of
![]() $[\kappa ]^\omega $
of cardinality less than
$[\kappa ]^\omega $
of cardinality less than
![]() $\mathfrak {r}$
that consists of cofinal sequences and has the property that for every closed unbounded subset C of
$\mathfrak {r}$
that consists of cofinal sequences and has the property that for every closed unbounded subset C of
![]() $\kappa $
such that the set
$\kappa $
such that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
, there exists
$A\cup \{\kappa \}$
, there exists
![]() $a\in A'$
with
$a\in A'$
with
![]() $a\subseteq C$
. Using Lemma 2.9, we can now find a subset E of
$a\subseteq C$
. Using Lemma 2.9, we can now find a subset E of
![]() $\kappa $
such that for every
$\kappa $
such that for every
![]() $a\in A$
, both
$a\in A$
, both
![]() $a\setminus E$
and
$a\setminus E$
and
![]() $a\cap E$
are infinite. Then, both E and
$a\cap E$
are infinite. Then, both E and
![]() $\kappa \setminus E$
are
$\kappa \setminus E$
are
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
.
$\kappa $
.
We close this section by comparing another aspect of the behavior of stationary sets with its counterpart in the definable context. While the collection of all closed unbounded subsets of a cardinal of uncountable cofinality is closed under intersections, and therefore, all of these subsets are stationary, these implications can obviously fail at a singular cardinal of countable cofinality, where all unbounded sets of order type
![]() $\omega $
are closed unbounded and stationarity coincides with coboundedness. The following lemma completely characterizes the settings in which these implications also hold in the definable context:
$\omega $
are closed unbounded and stationarity coincides with coboundedness. The following lemma completely characterizes the settings in which these implications also hold in the definable context:
Lemma 2.10 Given a class A and a natural number
![]() $n>0$
, the following statements are equivalent for every singular cardinal
$n>0$
, the following statements are equivalent for every singular cardinal
![]() $\kappa $
of countable cofinality:
$\kappa $
of countable cofinality:
-
(1) There is a cofinal function
 ${c}:{\omega }\longrightarrow {\kappa }$
that is definable by a
${c}:{\omega }\longrightarrow {\kappa }$
that is definable by a
 $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
 $A\cup \{\kappa \}$
.
$A\cup \{\kappa \}$
. -
(2) There are disjoint closed unbounded subsets
 $C_0$
and
$C_0$
and
 $C_1$
of
$C_1$
of
 $\kappa $
with the property that the sets
$\kappa $
with the property that the sets
 $\{C_0\}$
and
$\{C_0\}$
and
 $\{C_1\}$
are both definable by
$\{C_1\}$
are both definable by
 $\Sigma _n$
-formulas with parameters in
$\Sigma _n$
-formulas with parameters in
 $A\cup \{\kappa \}$
.
$A\cup \{\kappa \}$
. -
(3) There are closed unbounded subsets
 $C_0$
and
$C_0$
and
 $C_1$
of
$C_1$
of
 $\kappa $
with
$\kappa $
with
 $C_0\cap C_1$
bounded in
$C_0\cap C_1$
bounded in
 $\kappa $
and the property that the sets
$\kappa $
and the property that the sets
 $\{C_0\}$
and
$\{C_0\}$
and
 $\{C_1\}$
are both definable by
$\{C_1\}$
are both definable by
 $\Sigma _n$
-formulas with parameters in
$\Sigma _n$
-formulas with parameters in
 $A\cup \{\kappa \}$
.
$A\cup \{\kappa \}$
.
Proof First, we assume that there is a cofinal function
![]() ${c}:{\omega }\longrightarrow {\kappa }$
that is definable by a
${c}:{\omega }\longrightarrow {\kappa }$
that is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
. Define
$A\cup \{\kappa \}$
. Define
![]() $C_0=\{{c(n)+\omega }~\vert ~{n<\omega }\}$
and
$C_0=\{{c(n)+\omega }~\vert ~{n<\omega }\}$
and
![]() $C_1=\{{c(n)+\omega +1}~\vert ~{n<\omega }\}$
. Then,
$C_1=\{{c(n)+\omega +1}~\vert ~{n<\omega }\}$
. Then,
![]() $C_0$
and
$C_0$
and
![]() $C_1$
are disjoint closed unbounded in
$C_1$
are disjoint closed unbounded in
![]() $\kappa $
, and the sets
$\kappa $
, and the sets
![]() $\{C_0\}$
and
$\{C_0\}$
and
![]() $\{C_1\}$
are definable by
$\{C_1\}$
are definable by
![]() $\Sigma _n$
-formulas with parameters in
$\Sigma _n$
-formulas with parameters in
![]() $A\cup \{\kappa \}$
. In the other direction, assume that there are closed unbounded subsets
$A\cup \{\kappa \}$
. In the other direction, assume that there are closed unbounded subsets
![]() $C_0$
and
$C_0$
and
![]() $C_1$
of
$C_1$
of
![]() $\kappa $
with
$\kappa $
with
![]() $C_0\cap C_1$
bounded in
$C_0\cap C_1$
bounded in
![]() $\kappa $
and the property that the sets
$\kappa $
and the property that the sets
![]() $\{C_0\}$
and
$\{C_0\}$
and
![]() $\{C_1\}$
are both definable by
$\{C_1\}$
are both definable by
![]() $\Sigma _n$
-formulas with parameters in
$\Sigma _n$
-formulas with parameters in
![]() $A\cup \{\kappa \}$
. We define
$A\cup \{\kappa \}$
. We define
![]() $\mu =\max (C_0\cap C_1)<\kappa $
and let
$\mu =\max (C_0\cap C_1)<\kappa $
and let
![]() ${c}:{\omega }\longrightarrow {\kappa }$
denote the unique function with
${c}:{\omega }\longrightarrow {\kappa }$
denote the unique function with
![]() $c(0)=\mu $
and
$c(0)=\mu $
and
for all
![]() $k<\omega $
and
$k<\omega $
and
![]() $i<2$
. The
$i<2$
. The
![]() $\Sigma _n$
-Recursion Theorem then implies that c is definable by a
$\Sigma _n$
-Recursion Theorem then implies that c is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
. Moreover, we know that c is cofinal in
$A\cup \{\kappa \}$
. Moreover, we know that c is cofinal in
![]() $\kappa $
because otherwise,
$\kappa $
because otherwise,
![]() $\mu <\sup _{k<\omega }c(k)\in C_0\cap C_1$
.
$\mu <\sup _{k<\omega }c(k)\in C_0\cap C_1$
.
Using an argument similar to the one of the previous Lemma, we obtain the following corollary, which will later allow us to show that definable closed unbounded sets behave nicely in various settings.
Corollary 2.11 Let
![]() $\kappa $
be a singular cardinal of countable cofinality, let A be a class, and let
$\kappa $
be a singular cardinal of countable cofinality, let A be a class, and let
![]() $n>0$
be a natural number with the property that there exists a subset of
$n>0$
be a natural number with the property that there exists a subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _n(A)$
-stationary in
$\Sigma _n(A)$
-stationary in
![]() $\kappa $
and consists of cardinals. Then, the collection of all closed unbounded subsets C of
$\kappa $
and consists of cardinals. Then, the collection of all closed unbounded subsets C of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $A\cup \{\kappa \}$
is closed under intersections.
$A\cup \{\kappa \}$
is closed under intersections.
2.3 The
 $\boldsymbol {\Sigma }_n$
-undefinability property
$\boldsymbol {\Sigma }_n$
-undefinability property
We introduce a notion that will allow us to show that various nonstationary sets of cardinals
![]() $E \subseteq \kappa $
of an uncountable cardinal
$E \subseteq \kappa $
of an uncountable cardinal
![]() $\kappa $
are
$\kappa $
are
![]() $\boldsymbol {\Sigma }_n$
-stationary.
$\boldsymbol {\Sigma }_n$
-stationary.
Definition 2.2 Given uncountable cardinals
![]() $\mu <\kappa $
, an ordinal
$\mu <\kappa $
, an ordinal
![]() $\gamma \geq \kappa $
, and a natural number n, we say that the cardinal
$\gamma \geq \kappa $
, and a natural number n, we say that the cardinal
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _n(\mu ,\gamma )$
-undefinability property if no ordinal
$\Sigma _n(\mu ,\gamma )$
-undefinability property if no ordinal
![]() $\alpha $
in the interval
$\alpha $
in the interval
![]() $[\mu ,\kappa )$
has the property that the set
$[\mu ,\kappa )$
has the property that the set
![]() $\{\alpha \}$
is definable by a
$\{\alpha \}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in the set
$\Sigma _n$
-formula with parameters in the set
![]() $\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
. Moreover, we say that
$\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
. Moreover, we say that
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _n(\mu )$
-undefinability property if it has the
$\Sigma _n(\mu )$
-undefinability property if it has the
![]() $\Sigma _n(\mu ,\kappa )$
-undefinability property.
$\Sigma _n(\mu ,\kappa )$
-undefinability property.
The next lemma shows how this undefinability property is connected to
![]() $\Sigma _n$
-stationarity:
$\Sigma _n$
-stationarity:
Lemma 2.12 Given uncountable cardinals
![]() $\mu <\kappa $
, an ordinal
$\mu <\kappa $
, an ordinal
![]() $\gamma \geq \kappa $
, and a natural number
$\gamma \geq \kappa $
, and a natural number
![]() $n>0$
, if
$n>0$
, if
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _n(\mu ,\gamma )$
-undefinability property, then the set
$\Sigma _n(\mu ,\gamma )$
-undefinability property, then the set
![]() $\{\mu \}$
is
$\{\mu \}$
is
![]() $\Sigma _n(\mathrm {H}_{\mu }\cup \{\gamma \})$
-stationary in
$\Sigma _n(\mathrm {H}_{\mu }\cup \{\gamma \})$
-stationary in
![]() $\kappa $
.
$\kappa $
.
Proof Let C be a closed unbounded subset of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
. Assume, toward a contradiction, that
$\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
. Assume, toward a contradiction, that
![]() $\mu $
is not an element of C. Set
$\mu $
is not an element of C. Set
![]() $\nu =\min (C\setminus \mu )>\mu $
. Then,
$\nu =\min (C\setminus \mu )>\mu $
. Then,
![]() $C\cap \mu \neq \emptyset $
because otherwise,
$C\cap \mu \neq \emptyset $
because otherwise,
![]() $\nu =\min (C)$
, and this would imply that the set
$\nu =\min (C)$
, and this would imply that the set
![]() $\{\nu \}$
is definable by a
$\{\nu \}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
. This allows us to define
$\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
. This allows us to define
![]() $\rho =\max (C\cap \mu )<\mu $
. But then,
$\rho =\max (C\cap \mu )<\mu $
. But then,
![]() $\nu =\min (C\setminus (\rho +1))$
, and hence,
$\nu =\min (C\setminus (\rho +1))$
, and hence,
![]() $\{\nu \}$
is definable by a
$\{\nu \}$
is definable by a
![]() $\Sigma _n$
-formula with parameters in
$\Sigma _n$
-formula with parameters in
![]() $\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
, a contradiction.
$\mathrm {H}_{\mu }\cup \{\kappa ,\gamma \}$
, a contradiction.
The following direct corollary of the above lemma will later allow us to isolate various examples of
![]() $\boldsymbol {\Sigma }_1$
-stationary subsets of cardinals of countable cofinality that are not stationary (i.e., not cobounded) in the given limit cardinal.
$\boldsymbol {\Sigma }_1$
-stationary subsets of cardinals of countable cofinality that are not stationary (i.e., not cobounded) in the given limit cardinal.
Corollary 2.13 Let
![]() $\kappa $
be a limit cardinal, let
$\kappa $
be a limit cardinal, let
![]() $\gamma \geq \kappa $
be an ordinal, let
$\gamma \geq \kappa $
be an ordinal, let
![]() $n>0$
be a natural number, and let E be the set of uncountable cardinals
$n>0$
be a natural number, and let E be the set of uncountable cardinals
![]() $\mu <\kappa $
with the property that
$\mu <\kappa $
with the property that
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _n(\mu ,\gamma )$
-undefinability property for all
$\Sigma _n(\mu ,\gamma )$
-undefinability property for all
![]() $\mu \in E$
. If E is unbounded in
$\mu \in E$
. If E is unbounded in
![]() $\kappa $
, then E is
$\kappa $
, then E is
![]() $\boldsymbol {\Sigma }_n(\{\gamma \})$
-stationary in
$\boldsymbol {\Sigma }_n(\{\gamma \})$
-stationary in
![]() $\kappa $
.
$\kappa $
.
3 Undefinability in the Dodd-Jensen core model
In the following, we establish basic definability and undefinability results dealing with Dodd-Jensen core model
![]() $\mathrm {{K}}^{DJ}$
. These results make use of the presentation of this model in [Reference Donder and Koepke5] and [Reference Koepke11]. In this setting, a set M is a premouse at an ordinal
$\mathrm {{K}}^{DJ}$
. These results make use of the presentation of this model in [Reference Donder and Koepke5] and [Reference Koepke11]. In this setting, a set M is a premouse at an ordinal
![]() $\mu>\omega $
if M is of the form
$\mu>\omega $
if M is of the form
![]() $J^U_\eta $
and
$J^U_\eta $
and
Moreover, if M is a premouse at
![]() $\mu $
, then we define the lower part of M to be the set
$\mu $
, then we define the lower part of M to be the set
![]() $lp(M)=M\cap V_\mu $
. Given a premouse M and an ordinal
$lp(M)=M\cap V_\mu $
. Given a premouse M and an ordinal
![]() $\delta $
, an iteration of M of length
$\delta $
, an iteration of M of length
![]() $\delta $
is given by a sequence
$\delta $
is given by a sequence
![]() $\langle {M_\alpha }~\vert ~{\alpha <\delta }\rangle $
of premice and a commuting system
$\langle {M_\alpha }~\vert ~{\alpha <\delta }\rangle $
of premice and a commuting system
![]() $\langle {{j_{\alpha ,\beta }}:{M_\alpha }\longrightarrow {M_\beta }}~\vert ~{\alpha \leq \beta <\delta }\rangle $
of
$\langle {{j_{\alpha ,\beta }}:{M_\alpha }\longrightarrow {M_\beta }}~\vert ~{\alpha \leq \beta <\delta }\rangle $
of
![]() $\Sigma _1$
-elementary embeddings such that the following statements hold:
$\Sigma _1$
-elementary embeddings such that the following statements hold:
-
•
 $M=M_0$
and
$M=M_0$
and
 $j_{\alpha ,\alpha }=\mathrm {{id}}_{M_\alpha }$
for all
$j_{\alpha ,\alpha }=\mathrm {{id}}_{M_\alpha }$
for all
 $\alpha <\delta $
.
$\alpha <\delta $
. -
• If
 $\alpha +1<\delta $
,
$\alpha +1<\delta $
,
 $M_\alpha =J_\eta ^U$
is a premouse at
$M_\alpha =J_\eta ^U$
is a premouse at
 $\mu $
and
$\mu $
and
 $M_{\alpha +1}=J_\zeta ^W$
is a premouse at
$M_{\alpha +1}=J_\zeta ^W$
is a premouse at
 $\nu $
, then
$\nu $
, then
 $M_{\alpha +1}$
is the transitive collapse of the ultrapower of
$M_{\alpha +1}$
is the transitive collapse of the ultrapower of
 $M_\alpha $
using U,
$M_\alpha $
using U,
 $j_{\alpha ,\alpha +1}$
as the corresponding ultrapower embedding,
$j_{\alpha ,\alpha +1}$
as the corresponding ultrapower embedding,
 $j_{\alpha ,\alpha +1}(\mu )=\nu $
, and
$j_{\alpha ,\alpha +1}(\mu )=\nu $
, and  $$ \begin{align*}W ~ = ~ \{{[f]_U}~\vert~{f\in {}^\mu M_\alpha\cap M_\alpha, \{{\xi<\mu}~\vert~{f(\xi)\in U}\}\in U}\}.\end{align*} $$
$$ \begin{align*}W ~ = ~ \{{[f]_U}~\vert~{f\in {}^\mu M_\alpha\cap M_\alpha, \{{\xi<\mu}~\vert~{f(\xi)\in U}\}\in U}\}.\end{align*} $$
-
• If
 $\gamma \in \mathrm {{Lim}}\cap \delta $
, then
$\gamma \in \mathrm {{Lim}}\cap \delta $
, then
 $\langle M_\gamma ,\langle {{j_{\alpha ,\gamma }}:{M_\alpha }\longrightarrow {M_\gamma }}~\vert ~{\alpha <\gamma }\rangle \rangle $
is a direct limit of
$\langle M_\gamma ,\langle {{j_{\alpha ,\gamma }}:{M_\alpha }\longrightarrow {M_\gamma }}~\vert ~{\alpha <\gamma }\rangle \rangle $
is a direct limit of
 $\langle \langle {M_\alpha }~\vert ~{\alpha <\gamma }\rangle ,\langle {{j_{\alpha ,\beta }}:{M_\alpha }\longrightarrow {M_\beta }}~\vert ~{\alpha \leq \beta <\gamma }\rangle \rangle $
.
$\langle \langle {M_\alpha }~\vert ~{\alpha <\gamma }\rangle ,\langle {{j_{\alpha ,\beta }}:{M_\alpha }\longrightarrow {M_\beta }}~\vert ~{\alpha \leq \beta <\gamma }\rangle \rangle $
.
If such an iteration exists, then it is uniquely determined, and it is called the
![]() $\delta $
-iteration of M. A premouse M is then called a mouse if
$\delta $
-iteration of M. A premouse M is then called a mouse if
![]() $\delta $
-iterations of M exist for all
$\delta $
-iterations of M exist for all
![]() $\delta \in \mathrm {{\mathrm{Ord}}}$
. Note that since the iterability of a premouse can be checked in every transitive structure of uncountable ordinal height that contains the mouse and satisfies a sufficiently strong fragment of
$\delta \in \mathrm {{\mathrm{Ord}}}$
. Note that since the iterability of a premouse can be checked in every transitive structure of uncountable ordinal height that contains the mouse and satisfies a sufficiently strong fragment of
![]() $\mathrm {{ZFC}}$
(see [Reference Koepke11, Theorem 2.7]), it follows that the class of all mice is
$\mathrm {{ZFC}}$
(see [Reference Koepke11, Theorem 2.7]), it follows that the class of all mice is
![]() $\Sigma _1$
-definable from every uncountable ordinal. We can now use such iterations to compare a mouse
$\Sigma _1$
-definable from every uncountable ordinal. We can now use such iterations to compare a mouse
![]() $M=J^U_\eta $
at some ordinal
$M=J^U_\eta $
at some ordinal
![]() $\mu $
with a mouse
$\mu $
with a mouse
![]() $N=J^W_\zeta $
at an ordinal
$N=J^W_\zeta $
at an ordinal
![]() $\nu $
, in the sense that they allow us to find mice
$\nu $
, in the sense that they allow us to find mice
![]() $M^\prime =J^C_{\eta ^\prime }$
and
$M^\prime =J^C_{\eta ^\prime }$
and
![]() $N^\prime =J^C_{\zeta ^\prime }$
at the same ordinal
$N^\prime =J^C_{\zeta ^\prime }$
at the same ordinal
![]() $\rho $
and
$\rho $
and
![]() $\Sigma _1$
-elementary embeddings
$\Sigma _1$
-elementary embeddings
![]() ${j}:{M}\longrightarrow {M^\prime }$
and
${j}:{M}\longrightarrow {M^\prime }$
and
![]() ${i}:{N}\longrightarrow {N^\prime }$
with
${i}:{N}\longrightarrow {N^\prime }$
with
![]() $j(\mu )=i(\nu )=\rho $
(see [Reference Donder and Koepke5, Lemma 1.13]). In our arguments below, we will frequently make use of results of Dodd and Jensen (see [Reference Donder and Koepke5, pp. 238-241]) that show that the Dodd-Jensen core model
$j(\mu )=i(\nu )=\rho $
(see [Reference Donder and Koepke5, Lemma 1.13]). In our arguments below, we will frequently make use of results of Dodd and Jensen (see [Reference Donder and Koepke5, pp. 238-241]) that show that the Dodd-Jensen core model
![]() $\mathrm {{K}}^{DJ}$
is equal to the union of the constructible universe L and the lower parts
$\mathrm {{K}}^{DJ}$
is equal to the union of the constructible universe L and the lower parts
![]() $lp(M)$
of all mice M.
$lp(M)$
of all mice M.
We now prove three lemmata that show that various objects that witness the accessibility of cardinals in
![]() $\mathrm {{K}}^{DJ}$
are simply definable.
$\mathrm {{K}}^{DJ}$
are simply definable.
Lemma 3.1 If
![]() $\kappa $
is an infinite cardinal that is not inaccessible in
$\kappa $
is an infinite cardinal that is not inaccessible in
![]() $\mathrm {{K}}^{DJ}$
, then the set
$\mathrm {{K}}^{DJ}$
, then the set
![]() $\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
$\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
.
$\kappa $
.
Proof Since the
![]() $\mathrm {GCH}$
holds in
$\mathrm {GCH}$
holds in
![]() $\mathrm {K}^{DJ}$
and
$\mathrm {K}^{DJ}$
and
![]() $\mathrm {H}_{\aleph _0}^{\mathrm {K}^{DJ}} = \mathrm {L}_\omega $
, we may assume that either
$\mathrm {H}_{\aleph _0}^{\mathrm {K}^{DJ}} = \mathrm {L}_\omega $
, we may assume that either
![]() $\kappa $
is a successor cardinal in
$\kappa $
is a successor cardinal in
![]() $\mathrm {{K}}^{DJ}$
or
$\mathrm {{K}}^{DJ}$
or
![]() $\kappa $
is singular in
$\kappa $
is singular in
![]() $\mathrm {K}^{DJ}$
. Moreover, we may assume that there exists a mouse because otherwise,
$\mathrm {K}^{DJ}$
. Moreover, we may assume that there exists a mouse because otherwise,
![]() $\mathrm {K}^{DJ}=\mathrm {L}$
, and
$\mathrm {K}^{DJ}=\mathrm {L}$
, and
![]() $\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}=\{\mathrm {L}_{\kappa }\}$
is
$\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}=\{\mathrm {L}_{\kappa }\}$
is
![]() $\Sigma _1$
-definable in the desired way.
$\Sigma _1$
-definable in the desired way.
Claim If M is a mouse at some
![]() $\nu>\kappa $
such that
$\nu>\kappa $
such that
![]() $\kappa $
is either a successor cardinal or a singular cardinal in M, then
$\kappa $
is either a successor cardinal or a singular cardinal in M, then
![]() $\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\subseteq M$
.
$\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\subseteq M$
.
Proof of the Claim
Fix
![]() $x\in \mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}$
. Then, there exists a mouse
$x\in \mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}$
. Then, there exists a mouse
![]() $N_0$
at some cardinal
$N_0$
at some cardinal
![]() $\mu <\kappa $
such that
$\mu <\kappa $
such that
![]() $\vert {N_0}\vert <\kappa $
and
$\vert {N_0}\vert <\kappa $
and
![]() $x\in lp(N_0)$
. Let N be the mouse obtained by iterating the top measure of
$x\in lp(N_0)$
. Let N be the mouse obtained by iterating the top measure of
![]() $N_0$
$N_0$
![]() $\kappa $
-many times. Then clearly, we have
$\kappa $
-many times. Then clearly, we have
![]() $x \in lp(N)$
, and
$x \in lp(N)$
, and
![]() $\kappa $
is the critical point of the top measure of N and is therefore inaccessible in N. The coiteration of M and N, which can only involve the top measures of the two mice, results in
$\kappa $
is the critical point of the top measure of N and is therefore inaccessible in N. The coiteration of M and N, which can only involve the top measures of the two mice, results in
![]() $\Sigma _1$
-elementary embeddings
$\Sigma _1$
-elementary embeddings
![]() ${\pi _M}:{M}\longrightarrow {M^\prime }$
and
${\pi _M}:{M}\longrightarrow {M^\prime }$
and
![]() ${\pi _N}:{N}\longrightarrow {N^\prime }$
with the following properties:
${\pi _N}:{N}\longrightarrow {N^\prime }$
with the following properties:
-
•
 $\kappa $
is inaccessible in
$\kappa $
is inaccessible in
 $N^{\prime }$
, but not in
$N^{\prime }$
, but not in
 $M^{\prime }$
,
$M^{\prime }$
, -
•
 $x \in lp(N^{\prime })$
,
$x \in lp(N^{\prime })$
, -
•
 $\mathcal {P}(\kappa )^M = \mathcal {P}(\kappa )^{M'}$
, and
$\mathcal {P}(\kappa )^M = \mathcal {P}(\kappa )^{M'}$
, and -
• one of
 $M^\prime $
,
$M^\prime $
,
 $N^\prime $
is an initial segment of the other.
$N^\prime $
is an initial segment of the other.
It is therefore clear that
![]() $N^{\prime }$
must be an initial segment of
$N^{\prime }$
must be an initial segment of
![]() $M^{\prime }$
, from which we conclude that
$M^{\prime }$
, from which we conclude that
![]() $x \in \mathcal {P}^{M'}(\kappa )$
and therefore that
$x \in \mathcal {P}^{M'}(\kappa )$
and therefore that
![]() $x \in M$
.
$x \in M$
.
As outlined earlier, the assumption that
![]() $\mathrm {{K}}^{DJ}\neq \mathrm {{L}}$
implies that
$\mathrm {{K}}^{DJ}\neq \mathrm {{L}}$
implies that
![]() $\mathrm {{K}}^{DJ}$
is equal to the union of all lower parts of mice. In particular, there exists a mouse M at an ordinal above
$\mathrm {{K}}^{DJ}$
is equal to the union of all lower parts of mice. In particular, there exists a mouse M at an ordinal above
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $\kappa $
is either a successor cardinal or a singular cardinal in M. By the above claim, we know that
$\kappa $
is either a successor cardinal or a singular cardinal in M. By the above claim, we know that
![]() $\mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}=\mathrm {H}_{\kappa }^M$
holds for every mouse M with these properties. By combining this implication with earlier remarks about the definability of the class of all mice, we can derive the statement of the lemma.
$\mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}=\mathrm {H}_{\kappa }^M$
holds for every mouse M with these properties. By combining this implication with earlier remarks about the definability of the class of all mice, we can derive the statement of the lemma.
Lemma 3.2 If
![]() $\kappa $
is an infinite cardinal, then the set
$\kappa $
is an infinite cardinal, then the set
![]() $\{{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}\}$
is definable by a
$\{{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
.
$\kappa $
.
Proof This is trivial in the case
![]() $\kappa $
is not singular in
$\kappa $
is not singular in
![]() $\mathrm {{K}}^{DJ}$
. Assuming it is singular, we know that
$\mathrm {{K}}^{DJ}$
. Assuming it is singular, we know that
![]() ${\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
is the unique ordinal
${\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
is the unique ordinal
![]() $\xi <\kappa $
with the property that
$\xi <\kappa $
with the property that
![]() $\xi $
is regular in
$\xi $
is regular in
![]() $\mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}$
and
$\mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}$
and
![]() $\mathrm {{K}}^{DJ}$
contains a cofinal function
$\mathrm {{K}}^{DJ}$
contains a cofinal function
![]() ${c}:{\xi }\longrightarrow {\kappa }$
. Since the class
${c}:{\xi }\longrightarrow {\kappa }$
. Since the class
![]() $\mathrm {{K}}^{DJ}$
is definable by a
$\mathrm {{K}}^{DJ}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
(see, for example, the proof of [Reference Lücke14, Lemma 4.13]), we can apply Lemma 3.1 to conclude that the set
$\kappa $
(see, for example, the proof of [Reference Lücke14, Lemma 4.13]), we can apply Lemma 3.1 to conclude that the set
![]() $\{{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}\}$
is also definable by a
$\{{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}\}$
is also definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
.
$\kappa $
.
Lemma 3.3 If
![]() $\kappa $
is an infinite cardinal and c is the
$\kappa $
is an infinite cardinal and c is the
![]() $<_{\mathrm {{K}}^{DJ}}$
-least cofinal function from
$<_{\mathrm {{K}}^{DJ}}$
-least cofinal function from
![]() ${\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
to
${\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
to
![]() $\kappa $
in
$\kappa $
in
![]() $\mathrm {{K}}^{DJ}$
, then the set
$\mathrm {{K}}^{DJ}$
, then the set
![]() $\{c\}$
is definable by a
$\{c\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
.
$\kappa $
.
Proof This is an immediate consequence of the proof of [Reference Lücke and Schlicht16, Lemma 2.3], which shows that the collection of initial segments of the restriction of
![]() $<_{\mathrm {{K}}^{DJ}}$
to
$<_{\mathrm {{K}}^{DJ}}$
to
![]() ${\mathcal {P}}({\kappa })$
is definable by a
${\mathcal {P}}({\kappa })$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
, and Lemma 3.2 above.
$\kappa $
, and Lemma 3.2 above.
We now use the above results to show that, in the case of singular cardinals
![]() $\kappa $
of uncountable cardinality, the statement of Proposition 2.5 cannot be strengthened in
$\kappa $
of uncountable cardinality, the statement of Proposition 2.5 cannot be strengthened in
![]() $\mathrm {{ZFC}}$
. We will later improve this result to obtain
$\mathrm {{ZFC}}$
. We will later improve this result to obtain
![]() ${\mathrm {{cof}}(\kappa )}$
-many measurable cardinals from the existence of a singular cardinal
${\mathrm {{cof}}(\kappa )}$
-many measurable cardinals from the existence of a singular cardinal
![]() $\kappa $
of uncountable cofinality with the property that there exists a nonstationary
$\kappa $
of uncountable cofinality with the property that there exists a nonstationary
![]() $\boldsymbol {\Sigma }_1$
-stationary subset of
$\boldsymbol {\Sigma }_1$
-stationary subset of
![]() $\kappa $
(see Theorem 5.1 and Corollary 5.2 below).
$\kappa $
(see Theorem 5.1 and Corollary 5.2 below).
Corollary 3.4 Assume that there is no inner model with a measurable cardinal. If
![]() $\kappa $
is a singular cardinal of uncountable cofinality and S is
$\kappa $
is a singular cardinal of uncountable cofinality and S is
![]() $\Sigma _1({\mathcal {P}}({{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}))$
-stationary in
$\Sigma _1({\mathcal {P}}({{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}))$
-stationary in
![]() $\kappa $
, then S is a stationary subset of
$\kappa $
, then S is a stationary subset of
![]() $\kappa $
.
$\kappa $
.
Proof By our assumption, the results of [Reference Dodd and Jensen4] ensure that
![]() $\kappa $
is a singular cardinal in
$\kappa $
is a singular cardinal in
![]() $\mathrm {{K}}^{DJ}$
. Using Lemma 3.3, we find a closed unbounded subset
$\mathrm {{K}}^{DJ}$
. Using Lemma 3.3, we find a closed unbounded subset
![]() $C_0$
of
$C_0$
of
![]() $\kappa $
of order-type
$\kappa $
of order-type
![]() ${\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
with the property that both the set
${\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
with the property that both the set
![]() $\{C_0\}$
and the monotone enumeration of
$\{C_0\}$
and the monotone enumeration of
![]() $C_0$
are definable by a
$C_0$
are definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
. Given an arbitrary closed unbounded subset C of
$\kappa $
. Given an arbitrary closed unbounded subset C of
![]() $\kappa $
, we then know that the intersection
$\kappa $
, we then know that the intersection
![]() $C\cap C_0$
is a closed unbounded subset and the set
$C\cap C_0$
is a closed unbounded subset and the set
![]() $\{C\cap C_0\}$
is definable by a
$\{C\cap C_0\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${\mathcal {P}}({{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}})\cup \{\kappa \}$
. This shows that every subset of
${\mathcal {P}}({{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}})\cup \{\kappa \}$
. This shows that every subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _1({\mathcal {P}}({{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}))$
-stationary in
$\Sigma _1({\mathcal {P}}({{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}))$
-stationary in
![]() $\kappa $
is stationary in
$\kappa $
is stationary in
![]() $\kappa $
.
$\kappa $
.
We now derive further consequences of the above lemmata. The results of the subsequent sections will show that it is possible to use large cardinals to obtain singular cardinals
![]() $\kappa $
where the negations of all of the listed statements hold.
$\kappa $
where the negations of all of the listed statements hold.
Corollary 3.5 Assume that there is no inner model with a measurable cardinal. If
![]() $\kappa $
is a singular cardinal, then the following statements hold:
$\kappa $
is a singular cardinal, then the following statements hold:
-
(1) If
 $\alpha <\kappa $
, then the set
$\alpha <\kappa $
, then the set
 $\{\alpha \}$
is not
$\{\alpha \}$
is not
 $\Sigma _1(\alpha )$
-stationary in
$\Sigma _1(\alpha )$
-stationary in
 $\kappa $
.
$\kappa $
. -
(2) There is an unbounded subset of
 $\kappa $
that consists of cardinals and is not
$\kappa $
that consists of cardinals and is not
 $\Sigma _1$
-stationary.
$\Sigma _1$
-stationary. -
(3) There exists a regressive function
 ${r}:{\kappa }\longrightarrow {\kappa }$
that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
that is definable by a
 $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
 $\kappa $
and is not constant on any unbounded subset of
$\kappa $
and is not constant on any unbounded subset of
 $\kappa $
.
$\kappa $
.
Proof Set
![]() $\lambda ={\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
and let
$\lambda ={\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}$
and let
![]() ${c}:{\lambda }\longrightarrow {\kappa }$
denote the the
${c}:{\lambda }\longrightarrow {\kappa }$
denote the the
![]() $<_{\mathrm {{K}}^{DJ}}$
-least cofinal function from
$<_{\mathrm {{K}}^{DJ}}$
-least cofinal function from
![]() $\lambda $
to
$\lambda $
to
![]() $\kappa $
in
$\kappa $
in
![]() $\mathrm {{K}}^{DJ}$
. By our assumption, the results of [Reference Dodd and Jensen4] imply that
$\mathrm {{K}}^{DJ}$
. By our assumption, the results of [Reference Dodd and Jensen4] imply that
![]() $\lambda <\kappa $
, and we can use Lemma 3.1 to show that the set
$\lambda <\kappa $
, and we can use Lemma 3.1 to show that the set
![]() $\mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}$
is definable by a
$\mathrm {H}_{\kappa }^{\mathrm {{K}}^{DJ}}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
. Moreover, Lemma 3.2 and Lemma 3.3 ensure that both the set
$\kappa $
. Moreover, Lemma 3.2 and Lemma 3.3 ensure that both the set
![]() $\{\lambda \}$
and the function c are definable by a
$\{\lambda \}$
and the function c are definable by a
![]() $\Sigma _1$
-formulas with parameter
$\Sigma _1$
-formulas with parameter
![]() $\kappa $
.
$\kappa $
.
Now, fix
![]() $\alpha <\kappa $
. If
$\alpha <\kappa $
. If
![]() $\alpha \leq \lambda $
, then
$\alpha \leq \lambda $
, then
![]() $C=(\lambda ,\kappa )$
is a closed unbounded subset of
$C=(\lambda ,\kappa )$
is a closed unbounded subset of
![]() $\kappa $
that is disjoint from
$\kappa $
that is disjoint from
![]() $\{\alpha \}$
and has the property that the set
$\{\alpha \}$
and has the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
. In the other case, if
$\kappa $
. In the other case, if
![]() $\lambda <\alpha $
, then there is
$\lambda <\alpha $
, then there is
![]() $\xi <\lambda $
with
$\xi <\lambda $
with
![]() $c(\xi )>\alpha $
, and
$c(\xi )>\alpha $
, and
![]() $C=(c(\xi ),\kappa )$
is a closed unbounded subset of
$C=(c(\xi ),\kappa )$
is a closed unbounded subset of
![]() $\kappa $
disjoint from
$\kappa $
disjoint from
![]() $\{\alpha \}$
with the property that the set
$\{\alpha \}$
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\alpha \cup \{\kappa \}$
.
$\alpha \cup \{\kappa \}$
.
Next, assume that
![]() $\kappa $
is a limit of limit cardinals in
$\kappa $
is a limit of limit cardinals in
![]() $\mathrm {{K}}^{DJ}$
, and define C to be the closed unbounded set of all ordinals
$\mathrm {{K}}^{DJ}$
, and define C to be the closed unbounded set of all ordinals
![]() $\rho <\kappa $
with the property that, in
$\rho <\kappa $
with the property that, in
![]() $\mathrm {{K}}^{DJ}$
, the ordinal
$\mathrm {{K}}^{DJ}$
, the ordinal
![]() $\rho $
is a limit cardinal. Since the set
$\rho $
is a limit cardinal. Since the set
![]() $\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
$\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
, it follows that set
$\kappa $
, it follows that set
![]() $\{C\}$
is definable in the same way. Now, let E denote the set of all successor cardinals of singular cardinals smaller than
$\{C\}$
is definable in the same way. Now, let E denote the set of all successor cardinals of singular cardinals smaller than
![]() $\kappa $
. Since our setup and the results of [Reference Dodd and Jensen4] ensure that all singular cardinals are singular in
$\kappa $
. Since our setup and the results of [Reference Dodd and Jensen4] ensure that all singular cardinals are singular in
![]() $\mathrm {K}^{DJ}$
and
$\mathrm {K}^{DJ}$
and
![]() $\mathrm {K}^{DJ}$
computes the successors of these cardinals correctly, we know that each element of E is the successor of a singular cardinal in
$\mathrm {K}^{DJ}$
computes the successors of these cardinals correctly, we know that each element of E is the successor of a singular cardinal in
![]() $\mathrm {K}^{DJ}$
, and this shows that
$\mathrm {K}^{DJ}$
, and this shows that
![]() $C\cap E=\emptyset $
. In particular, we can conclude that E is an unbounded subset of
$C\cap E=\emptyset $
. In particular, we can conclude that E is an unbounded subset of
![]() $\kappa $
that consists of cardinals and is not
$\kappa $
that consists of cardinals and is not
![]() $\Sigma _1$
-stationary.
$\Sigma _1$
-stationary.
We now assume that
![]() $\kappa $
is not a limit of limit cardinals in
$\kappa $
is not a limit of limit cardinals in
![]() $\mathrm {K}^{DJ}$
. Let
$\mathrm {K}^{DJ}$
. Let
![]() $\eta $
denote the least ordinal below
$\eta $
denote the least ordinal below
![]() $\kappa $
with the property that the interval
$\kappa $
with the property that the interval
![]() $(\eta ,\kappa )$
contains no ordinals that are limit cardinals in
$(\eta ,\kappa )$
contains no ordinals that are limit cardinals in
![]() $\mathrm {K}^{DJ}$
, and we define C to be the set of ordinals in
$\mathrm {K}^{DJ}$
, and we define C to be the set of ordinals in
![]() $(\eta ,\kappa )$
that are successor ordinals of ordinals that are cardinals in
$(\eta ,\kappa )$
that are successor ordinals of ordinals that are cardinals in
![]() $\mathrm {K}^{DJ}$
. Our assumptions then imply that C is a cofinal subset of
$\mathrm {K}^{DJ}$
. Our assumptions then imply that C is a cofinal subset of
![]() $\kappa $
of order-type
$\kappa $
of order-type
![]() $\omega $
, and this implies that C is a closed unbounded subset of
$\omega $
, and this implies that C is a closed unbounded subset of
![]() $\kappa $
. Moreover, the fact that the set
$\kappa $
. Moreover, the fact that the set
![]() $\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
$\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
ensures that the set
$\kappa $
ensures that the set
![]() $\{C\}$
is definable in the same way. If we now define E to be the set of all cardinals in the interval
$\{C\}$
is definable in the same way. If we now define E to be the set of all cardinals in the interval
![]() $(\eta ,\kappa )$
, then E is unbounded in
$(\eta ,\kappa )$
, then E is unbounded in
![]() $\kappa $
, and since
$\kappa $
, and since
![]() $C\cap E=\emptyset $
holds, we know that E is not
$C\cap E=\emptyset $
holds, we know that E is not
![]() $\Sigma _1$
-stationary.
$\Sigma _1$
-stationary.
Finally, define
![]() ${r}:{\kappa }\longrightarrow {\lambda }$
to be the unique map with
${r}:{\kappa }\longrightarrow {\lambda }$
to be the unique map with
![]() $c(\alpha )=0$
for all
$c(\alpha )=0$
for all
![]() $\alpha <\lambda $
and
$\alpha <\lambda $
and
![]() $c(\alpha )=\min \{{\xi <\lambda }~\vert ~{c(\xi )\geq \alpha }\}$
for all
$c(\alpha )=\min \{{\xi <\lambda }~\vert ~{c(\xi )\geq \alpha }\}$
for all
![]() $\lambda \leq \alpha <\kappa $
. Then, r is regressive, and it is not constant on any unbounded subset of
$\lambda \leq \alpha <\kappa $
. Then, r is regressive, and it is not constant on any unbounded subset of
![]() $\kappa $
. Moreover, our earlier observations show that r is definable by a
$\kappa $
. Moreover, our earlier observations show that r is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
.
$\kappa $
.
Corollary 3.6 Assume that there is no inner model with a measurable cardinal. If
![]() $\kappa $
is a singular cardinal of countable cofinality, then the following statements hold:
$\kappa $
is a singular cardinal of countable cofinality, then the following statements hold:
-
(1) There are disjoint closed unbounded subsets
 $C_0$
and
$C_0$
and
 $C_1$
of
$C_1$
of
 $\kappa $
with the property that the sets
$\kappa $
with the property that the sets
 $\{C_0\}$
and
$\{C_0\}$
and
 $\{C_1\}$
are both definable by
$\{C_1\}$
are both definable by
 $\Sigma _1$
-formulas with parameters in
$\Sigma _1$
-formulas with parameters in
 $\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. -
(2) There exists a subset A of
 $\mathrm {H}_{\kappa }$
of cardinality
$\mathrm {H}_{\kappa }$
of cardinality
 $\mathfrak {r}$
such that every subset of
$\mathfrak {r}$
such that every subset of
 $\kappa $
that is
$\kappa $
that is
 $\Sigma _1(A)$
-stationary in
$\Sigma _1(A)$
-stationary in
 $\kappa $
contains a closed unbounded subset C of
$\kappa $
contains a closed unbounded subset C of
 $\kappa $
with the property that the set
$\kappa $
with the property that the set
 $\{C\}$
is definable by a
$\{C\}$
is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 $A\cup \{\kappa \}$
.
$A\cup \{\kappa \}$
.
Proof Set
![]() $\lambda ={\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^DJ}$
. Our assumptions then imply that
$\lambda ={\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^DJ}$
. Our assumptions then imply that
![]() $\lambda <\kappa $
. Let
$\lambda <\kappa $
. Let
![]() ${c}:{\lambda }\longrightarrow {\kappa }$
denote the
${c}:{\lambda }\longrightarrow {\kappa }$
denote the
![]() $<_{\mathrm {{K}}^{DJ}}$
-least cofinal function in
$<_{\mathrm {{K}}^{DJ}}$
-least cofinal function in
![]() $\mathrm {{K}}^{DJ}$
. Since
$\mathrm {{K}}^{DJ}$
. Since
![]() ${\mathrm {{cof}}(\lambda )}=\omega $
, we can also fix a cofinal function
${\mathrm {{cof}}(\lambda )}=\omega $
, we can also fix a cofinal function
![]() ${d}:{\omega }\longrightarrow {\lambda }$
. Define
${d}:{\omega }\longrightarrow {\lambda }$
. Define
![]() $C_0=\{{\omega \cdot ((c\circ d)(i))}~\vert ~{i<\omega }\}$
and
$C_0=\{{\omega \cdot ((c\circ d)(i))}~\vert ~{i<\omega }\}$
and
![]() $C_1=\{{\alpha +1}~\vert ~{\alpha \in C_0}\}$
. Then, the sets
$C_1=\{{\alpha +1}~\vert ~{\alpha \in C_0}\}$
. Then, the sets
![]() $C_0$
and
$C_0$
and
![]() $C_1$
are disjoint closed unbounded subsets of
$C_1$
are disjoint closed unbounded subsets of
![]() $\kappa $
. Moreover, Lemma 3.3 ensures that the sets
$\kappa $
. Moreover, Lemma 3.3 ensures that the sets
![]() $\{C_0\}$
and
$\{C_0\}$
and
![]() $\{C_1\}$
are both definable by
$\{C_1\}$
are both definable by
![]() $\Sigma _1$
-formulas with parameters
$\Sigma _1$
-formulas with parameters
![]() $\kappa $
and d. Finally, pick a subset A of
$\kappa $
and d. Finally, pick a subset A of
![]() $\mathrm {H}_{\kappa }$
of cardinality
$\mathrm {H}_{\kappa }$
of cardinality
![]() $\mathfrak {r}$
such that
$\mathfrak {r}$
such that
![]() $\omega \cup \{d\}\subseteq A$
,
$\omega \cup \{d\}\subseteq A$
,
![]() $A\cap \kappa $
is cofinal in
$A\cap \kappa $
is cofinal in
![]() $\kappa $
, and for every
$\kappa $
, and for every
![]() $b\in [\omega ]^\omega $
, there is
$b\in [\omega ]^\omega $
, there is
![]() $a\in A\cap [\omega ]^\omega $
with the property that either
$a\in A\cap [\omega ]^\omega $
with the property that either
![]() $a\setminus b$
or
$a\setminus b$
or
![]() $a\cap b$
is finite. Let S be a subset of
$a\cap b$
is finite. Let S be a subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\Sigma _1(A)$
-stationary in
$\Sigma _1(A)$
-stationary in
![]() $\kappa $
. The fact that
$\kappa $
. The fact that
![]() $A\cap \kappa $
is unbounded in
$A\cap \kappa $
is unbounded in
![]() $\kappa $
then implies that the set
$\kappa $
then implies that the set
![]() $b=\{{i<\omega }~\vert ~{(c\circ d)(i)\in S}\}$
is infinite. Hence, there exists
$b=\{{i<\omega }~\vert ~{(c\circ d)(i)\in S}\}$
is infinite. Hence, there exists
![]() $a\in A$
with the property that either
$a\in A$
with the property that either
![]() $a\setminus b$
or
$a\setminus b$
or
![]() $a\cap b$
is finite. Set
$a\cap b$
is finite. Set
![]() $C=\{{(c\circ d)(i)}~\vert ~{i\in a}\}$
. Then, C is closed unbounded in
$C=\{{(c\circ d)(i)}~\vert ~{i\in a}\}$
. Then, C is closed unbounded in
![]() $\kappa $
, and the set
$\kappa $
, and the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $A\cup \{\kappa \}$
. Hence, we know that
$A\cup \{\kappa \}$
. Hence, we know that
![]() $C\cap S$
is unbounded in
$C\cap S$
is unbounded in
![]() $\kappa $
, and this shows that
$\kappa $
, and this shows that
![]() $a\cap b$
is infinite. We can now find
$a\cap b$
is infinite. We can now find
![]() $k<\omega $
with
$k<\omega $
with
![]() $a\setminus b\subseteq k$
, and if we define
$a\setminus b\subseteq k$
, and if we define
![]() $D=\{{(c\circ d)(i)}~\vert ~{k\leq i\in A}\}$
, then D is a closed unbounded subset of S and the set
$D=\{{(c\circ d)(i)}~\vert ~{k\leq i\in A}\}$
, then D is a closed unbounded subset of S and the set
![]() $\{D\}$
is definable by a
$\{D\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $A\cup \{\kappa \}$
.
$A\cup \{\kappa \}$
.
We end this section with another result about the definability of initial segments of the Dodd-Jensen core model that will be used in our characterizations of stably measurable cardinals below.
Lemma 3.7 Let
![]() $\kappa $
be an uncountable cardinal, and let
$\kappa $
be an uncountable cardinal, and let
![]() $E\in \mathrm {{K}}^{DJ}$
be a subset of
$E\in \mathrm {{K}}^{DJ}$
be a subset of
![]() $\kappa $
. If
$\kappa $
. If
![]() $\kappa $
is regular in
$\kappa $
is regular in
![]() $\mathrm {{K}}^{DJ}$
and E is a bistationary subset of
$\mathrm {{K}}^{DJ}$
and E is a bistationary subset of
![]() $\kappa $
in
$\kappa $
in
![]() $\mathrm {{K}}^{DJ}$
, then the set
$\mathrm {{K}}^{DJ}$
, then the set
![]() $\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
$\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter E.
$\Sigma _1$
-formula with parameter E.
Proof Since the class
![]() $\mathrm {{K}}^{DJ}$
is definable by a
$\mathrm {{K}}^{DJ}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
in V, we may assume that
$\kappa $
in V, we may assume that
![]() $V=\mathrm {{K}}^{DJ}$
holds. Moreover, we may assume that there exists a mouse because otherwise, we have
$V=\mathrm {{K}}^{DJ}$
holds. Moreover, we may assume that there exists a mouse because otherwise, we have
![]() $\mathrm {K}^{DJ}=\mathrm {L}$
, and
$\mathrm {K}^{DJ}=\mathrm {L}$
, and
![]() $\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}=\{\mathrm {L}_\kappa \}$
is definable by a
$\{\mathrm {H}_{\kappa }^{\mathrm {K}^{DJ}}\}=\{\mathrm {L}_\kappa \}$
is definable by a
![]() $\Sigma _1$
-formula with parameter E. 2 The desired statement is then a direct consequence of the following observation:
$\Sigma _1$
-formula with parameter E. 2 The desired statement is then a direct consequence of the following observation:
Claim If M is a mouse with
![]() $E\in lp(M)$
, then
$E\in lp(M)$
, then
![]() $\mathrm {H}_{\kappa }\subseteq M$
.
$\mathrm {H}_{\kappa }\subseteq M$
.
Proof of the Claim
Assume, toward a contradiction, that there is an
![]() $x\in \mathrm {H}_{\kappa }\setminus M$
. Then, there is a mouse
$x\in \mathrm {H}_{\kappa }\setminus M$
. Then, there is a mouse
![]() $N_0$
with
$N_0$
with
![]() $\vert {N_0}\vert <\kappa $
and
$\vert {N_0}\vert <\kappa $
and
![]() $x\in lp(N_0)$
. As above, this allows us to find a mouse N at
$x\in lp(N_0)$
. As above, this allows us to find a mouse N at
![]() $\kappa $
with
$\kappa $
with
![]() $x\in lp(N)$
. Let
$x\in lp(N)$
. Let
![]() ${\pi _0}:{M}\longrightarrow {M^\prime }$
and
${\pi _0}:{M}\longrightarrow {M^\prime }$
and
![]() ${\pi _1}:{N}\longrightarrow {N^\prime }$
be the
${\pi _1}:{N}\longrightarrow {N^\prime }$
be the
![]() $\Sigma _1$
-elementary embeddings obtained by coiterating M and N (i.e., either
$\Sigma _1$
-elementary embeddings obtained by coiterating M and N (i.e., either
![]() $M^\prime $
is an initial segment of
$M^\prime $
is an initial segment of
![]() $N^\prime $
or
$N^\prime $
or
![]() $N^\prime $
is an initial segment of
$N^\prime $
is an initial segment of
![]() $M^\prime $
). Since
$M^\prime $
). Since
![]() $\mathrm {H}_{\kappa }^M=\mathrm {H}_{\kappa }^{M^\prime }$
and
$\mathrm {H}_{\kappa }^M=\mathrm {H}_{\kappa }^{M^\prime }$
and
![]() $x\in lp(N)\setminus M$
, we now know that
$x\in lp(N)\setminus M$
, we now know that
![]() $M^\prime $
is an initial segment of
$M^\prime $
is an initial segment of
![]() $N^\prime $
. This implies that
$N^\prime $
. This implies that
![]() $E\in {\mathcal {P}}({\kappa })^M={\mathcal {P}}({\kappa })^{M^\prime }\subseteq {\mathcal {P}}({\kappa })^{N^\prime }={\mathcal {P}}({\kappa })^N$
. Since the given N-ultrafilter on
$E\in {\mathcal {P}}({\kappa })^M={\mathcal {P}}({\kappa })^{M^\prime }\subseteq {\mathcal {P}}({\kappa })^{N^\prime }={\mathcal {P}}({\kappa })^N$
. Since the given N-ultrafilter on
![]() $\kappa $
is equal to the restriction of the closed unbounded filter on
$\kappa $
is equal to the restriction of the closed unbounded filter on
![]() $\kappa $
to
$\kappa $
to
![]() ${\mathcal {P}}({\kappa })^N$
, we can conclude that E either contains a closed unbounded subset of
${\mathcal {P}}({\kappa })^N$
, we can conclude that E either contains a closed unbounded subset of
![]() $\kappa $
or is disjoint from such a subset. This contradicts the bistationarity of E.
$\kappa $
or is disjoint from such a subset. This contradicts the bistationarity of E.
This claim now shows that
![]() $\mathrm {H}_{\kappa }$
is the unique set B with the property that there exists a mouse M with
$\mathrm {H}_{\kappa }$
is the unique set B with the property that there exists a mouse M with
![]() $E\in lp(M)$
and
$E\in lp(M)$
and
![]() $B=\mathrm {H}_{\kappa }^M$
. This directly yields the desired
$B=\mathrm {H}_{\kappa }^M$
. This directly yields the desired
![]() $\Sigma _1$
-definition of
$\Sigma _1$
-definition of
![]() $\{\mathrm {H}_{\kappa }\}$
.
$\{\mathrm {H}_{\kappa }\}$
.
4 Large cardinals and
 $\Sigma _1$
-stationary sets
$\Sigma _1$
-stationary sets
In Section 2, we already gave examples of two important features of
![]() $\Sigma _1(A)$
-stationary sets. First, the collection of these sets can be substantially larger than the collection of ordinary stationary sets. Second, this collection can possess structural features that resemble the behavior of stationary sets. We start by proving results for large cardinals and then extend these results to limits of large cardinals (not necessarily regular). Finally, we show that it is possible to derive similar consequences from Ramsey-theoretic properties that may hold on smaller cardinals.
$\Sigma _1(A)$
-stationary sets. First, the collection of these sets can be substantially larger than the collection of ordinary stationary sets. Second, this collection can possess structural features that resemble the behavior of stationary sets. We start by proving results for large cardinals and then extend these results to limits of large cardinals (not necessarily regular). Finally, we show that it is possible to derive similar consequences from Ramsey-theoretic properties that may hold on smaller cardinals.
4.1 Stably measurable cardinals
The following large cardinal property, introduced by Welch in [Reference Welch19], turns out to be closely connected to
![]() $\Sigma _1$
-undefinability considerations.
$\Sigma _1$
-undefinability considerations.
Definition 4.1 (Welch)
An uncountable regular cardinal
![]() $\kappa $
is stably measurable if there exists
$\kappa $
is stably measurable if there exists
-
• a transitive set M with
 $\mathrm {H}_{\kappa }\cup \{\kappa \}\subseteq M\prec _{\Sigma _1}\mathrm {H}_{\kappa ^+}$
,
$\mathrm {H}_{\kappa }\cup \{\kappa \}\subseteq M\prec _{\Sigma _1}\mathrm {H}_{\kappa ^+}$
, -
• a transitive set N with
 $M\cup {}^{{<}\kappa }N\subseteq N$
, and
$M\cup {}^{{<}\kappa }N\subseteq N$
, and -
• a normal, weakly amenable N-ultrafilter F on
 $\kappa $
with the property that
$\kappa $
with the property that
 $\langle N,\in ,F\rangle $
is iterable.
$\langle N,\in ,F\rangle $
is iterable.
In [Reference Sharpe and Welch17], Sharpe and Welch defined an uncountable cardinal
![]() $\kappa $
to be iterable if for every subset A of
$\kappa $
to be iterable if for every subset A of
![]() $\kappa $
, there is a transitive model M of
$\kappa $
, there is a transitive model M of
![]() $\mathrm {{ZFC}}^-$
of cardinality
$\mathrm {{ZFC}}^-$
of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $A,\kappa \in M$
and a weakly amenable M-ultrafilter U on
$A,\kappa \in M$
and a weakly amenable M-ultrafilter U on
![]() $\kappa $
such that
$\kappa $
such that
![]() $\langle M,\in ,U\rangle $
is
$\langle M,\in ,U\rangle $
is
![]() $\omega _1$
-iterable. It is easy to see that all iterable cardinals are stably measurable. Moreover, all Ramsey cardinals are iterable (see [Reference Sharpe and Welch17, Lemma 5.2]), and this shows that all measurable cardinals are stably measurable. In the other direction, [Reference Welch19, Corollary 1.18] shows that if
$\omega _1$
-iterable. It is easy to see that all iterable cardinals are stably measurable. Moreover, all Ramsey cardinals are iterable (see [Reference Sharpe and Welch17, Lemma 5.2]), and this shows that all measurable cardinals are stably measurable. In the other direction, [Reference Welch19, Corollary 1.18] shows that if
![]() $\kappa $
is a stably measurable cardinal, then
$\kappa $
is a stably measurable cardinal, then
![]() $a^\#$
exists for every set of ordinals a in
$a^\#$
exists for every set of ordinals a in
![]() $\mathrm {H}_{\kappa }$
. Motivated by Corollary 3.5, we proceed toward the following result:
$\mathrm {H}_{\kappa }$
. Motivated by Corollary 3.5, we proceed toward the following result:
Theorem 4.1 Let
![]() $\kappa $
be a stably measurable cardinal.
$\kappa $
be a stably measurable cardinal.
-
(1) If
 $\mu <\kappa $
is an uncountable cardinal, then the singleton
$\mu <\kappa $
is an uncountable cardinal, then the singleton
 $\{\mu \}$
is
$\{\mu \}$
is
 $\Sigma _1(\mathrm {H}_{\mu })$
-stationary in
$\Sigma _1(\mathrm {H}_{\mu })$
-stationary in
 $\kappa $
.
$\kappa $
. -
(2) If E is an unbounded subset of
 $\kappa $
that consists of cardinals, then E is
$\kappa $
that consists of cardinals, then E is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
.
$\kappa $
. -
(3) If S is a
 $\boldsymbol {\Sigma }_1$
-stationary subset of
$\boldsymbol {\Sigma }_1$
-stationary subset of
 $\kappa $
and
$\kappa $
and
 ${r}:{\kappa }\longrightarrow {\kappa }$
is a regressive function that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
is a regressive function that is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 $\mathrm {H}_{\kappa }\cup \{\kappa \}$
, then r is constant on a
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
, then r is constant on a
 $\boldsymbol {\Sigma }_1$
-stationary subset of S.
$\boldsymbol {\Sigma }_1$
-stationary subset of S.
Using Lemma 2.12 and Corollary 2.13, the first two statements of Theorem 4.1 directly follow from the next lemma:
Lemma 4.2 If
![]() $\kappa $
is a stably measurable cardinal, then
$\kappa $
is a stably measurable cardinal, then
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _1(\mu )$
-undefinability property for every uncountable cardinal
$\Sigma _1(\mu )$
-undefinability property for every uncountable cardinal
![]() $\mu <\kappa $
.
$\mu <\kappa $
.
Proof Assume, toward a contradiction, that there is a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
, an uncountable cardinal
$\varphi (v_0,v_1,v_2)$
, an uncountable cardinal
![]() $\mu <\kappa $
, an ordinal
$\mu <\kappa $
, an ordinal
![]() $\alpha $
in the interval
$\alpha $
in the interval
![]() $[\mu ,\kappa )$
, and
$[\mu ,\kappa )$
, and
![]() $z\in \mathrm {H}_{\mu }$
such that
$z\in \mathrm {H}_{\mu }$
such that
![]() $\alpha $
is the unique ordinal
$\alpha $
is the unique ordinal
![]() $\xi $
with the property that
$\xi $
with the property that
![]() $\varphi (\xi ,\kappa ,z)$
holds. Pick a transitive set M with
$\varphi (\xi ,\kappa ,z)$
holds. Pick a transitive set M with
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}\subseteq M\prec _{\Sigma _1}\mathrm {H}_{\kappa ^+}$
, a transitive set N with
$\mathrm {H}_{\kappa }\cup \{\kappa \}\subseteq M\prec _{\Sigma _1}\mathrm {H}_{\kappa ^+}$
, a transitive set N with
![]() $M\cup {}^{{<}\kappa }N\subseteq N$
, and a weakly amenable N-ultrafilter F on
$M\cup {}^{{<}\kappa }N\subseteq N$
, and a weakly amenable N-ultrafilter F on
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $\langle N,\in ,F\rangle $
is iterable. Now, pick an elementary submodel
$\langle N,\in ,F\rangle $
is iterable. Now, pick an elementary submodel
![]() $\langle X,\in ,F_0\rangle $
of
$\langle X,\in ,F_0\rangle $
of
![]() $\langle N,\in ,F\rangle $
of cardinality less than
$\langle N,\in ,F\rangle $
of cardinality less than
![]() $\mu $
with
$\mu $
with
![]() $\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
, and let
$\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
, and let
![]() ${\pi }:{X}\longrightarrow {N_0}$
denote the corresponding transitive collapse. Then,
${\pi }:{X}\longrightarrow {N_0}$
denote the corresponding transitive collapse. Then,
![]() $\pi (z)=z$
and
$\pi (z)=z$
and
![]() $\pi (\alpha )<\pi (\kappa )<\mu \leq \alpha $
. Moreover, if we set
$\pi (\alpha )<\pi (\kappa )<\mu \leq \alpha $
. Moreover, if we set
![]() $U=\pi [F_0]$
, then U is a weakly amenable
$U=\pi [F_0]$
, then U is a weakly amenable
![]() $N_0$
-ultrafilter on
$N_0$
-ultrafilter on
![]() $\pi (\kappa )$
and [Reference Kanamori10, Theorem 19.15] implies that
$\pi (\kappa )$
and [Reference Kanamori10, Theorem 19.15] implies that
![]() $\langle N_0,\in ,U\rangle $
is iterable. This yields a transitive set
$\langle N_0,\in ,U\rangle $
is iterable. This yields a transitive set
![]() $N_1$
and an elementary embedding
$N_1$
and an elementary embedding
![]() ${j}:{N_0}\longrightarrow {N_1}$
with
${j}:{N_0}\longrightarrow {N_1}$
with
![]() $j(\pi (\kappa ))=\kappa $
and
$j(\pi (\kappa ))=\kappa $
and
![]() $j\restriction \mathrm {H}_{\pi (\kappa )}^{N_0}=\mathrm {{id}}_{\mathrm {{H}_{\pi (\kappa )}^{N_0}}}$
. Since our setup ensures that
$j\restriction \mathrm {H}_{\pi (\kappa )}^{N_0}=\mathrm {{id}}_{\mathrm {{H}_{\pi (\kappa )}^{N_0}}}$
. Since our setup ensures that
![]() $\varphi (\alpha ,\kappa ,z)$
holds in N, we now know that
$\varphi (\alpha ,\kappa ,z)$
holds in N, we now know that
![]() $\varphi (\pi (\alpha ),\kappa ,z)$
holds in
$\varphi (\pi (\alpha ),\kappa ,z)$
holds in
![]() $N_1$
. By
$N_1$
. By
![]() $\Sigma _1$
-upwards absoluteness, this shows that
$\Sigma _1$
-upwards absoluteness, this shows that
![]() $\varphi (\pi (\alpha ),\kappa ,z)$
holds in
$\varphi (\pi (\alpha ),\kappa ,z)$
holds in
![]() $\mathrm {{V}}$
, contradicting the uniqueness of
$\mathrm {{V}}$
, contradicting the uniqueness of
![]() $\alpha $
.
$\alpha $
.
We now work toward a proof of the third part of Theorem 4.1. The starting point for this is a result of Welch (see [Reference Welch19, Theorem 1.26]) proving that stably measurable cardinals have the
![]() $\boldsymbol {\Sigma }_1$
-club property introduced in [Reference Lücke14] (i.e., if
$\boldsymbol {\Sigma }_1$
-club property introduced in [Reference Lücke14] (i.e., if
![]() $\kappa $
is a stably measurable cardinal and E is a subset of
$\kappa $
is a stably measurable cardinal and E is a subset of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{E\}$
is definable by a
$\{E\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
, then either E or
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
, then either E or
![]() $\kappa \setminus E$
contains a closed unbounded subset of
$\kappa \setminus E$
contains a closed unbounded subset of
![]() $\kappa $
). This result directly implies that if
$\kappa $
). This result directly implies that if
![]() $\kappa $
is a stably measurable cardinal and
$\kappa $
is a stably measurable cardinal and
![]() ${r}:{\kappa }\longrightarrow {\kappa }$
is a regressive function that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
is a regressive function that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
, then for every ordinal
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
, then for every ordinal
![]() $\alpha <\kappa $
, there is a closed unbounded subset
$\alpha <\kappa $
, there is a closed unbounded subset
![]() $C_\alpha $
of
$C_\alpha $
of
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $C_\alpha $
is either contained in
$C_\alpha $
is either contained in
![]() $r^{{-}1}\{\alpha \}$
or disjoint from
$r^{{-}1}\{\alpha \}$
or disjoint from
![]() $r^{{-}1}\{\alpha \}$
. By forming the diagonal intersection
$r^{{-}1}\{\alpha \}$
. By forming the diagonal intersection
![]() $\triangle _{\alpha <\kappa } C_\alpha $
, it is now easy to see that there is a unique ordinal
$\triangle _{\alpha <\kappa } C_\alpha $
, it is now easy to see that there is a unique ordinal
![]() $\alpha _*<\kappa $
with the property that
$\alpha _*<\kappa $
with the property that
![]() $C_{\alpha _*}\subseteq r^{{-}1}\{\alpha _*\}$
, and this directly implies that
$C_{\alpha _*}\subseteq r^{{-}1}\{\alpha _*\}$
, and this directly implies that
![]() $\alpha _*$
is the unique ordinal smaller than
$\alpha _*$
is the unique ordinal smaller than
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $r^{{-}1}\{\alpha _*\}$
contains a closed unbounded subset of
$r^{{-}1}\{\alpha _*\}$
contains a closed unbounded subset of
![]() $\kappa $
. The following lemma further strengthens this conclusion:
$\kappa $
. The following lemma further strengthens this conclusion:
Lemma 4.3 Let
![]() $\kappa $
be a stably measurable cardinal, and let E be a subset of
$\kappa $
be a stably measurable cardinal, and let E be a subset of
![]() $\kappa $
that contains a closed unbounded subset of
$\kappa $
that contains a closed unbounded subset of
![]() $\kappa $
and has the property that the set
$\kappa $
and has the property that the set
![]() $\{E\}$
is definable by a
$\{E\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Then, there exists a closed unbounded subset C of
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Then, there exists a closed unbounded subset C of
![]() $\kappa $
with
$\kappa $
with
![]() $C\subseteq E$
and the property that the set
$C\subseteq E$
and the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
Proof Fix a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
and an element z of
$\varphi (v_0,v_1,v_2)$
and an element z of
![]() $\mathrm {H}_{\kappa }$
with the property that the set
$\mathrm {H}_{\kappa }$
with the property that the set
![]() $\{E\}$
is definable by the formula
$\{E\}$
is definable by the formula
![]() $\varphi (v_0,v_1,v_2)$
and the parameters
$\varphi (v_0,v_1,v_2)$
and the parameters
![]() $\kappa $
and z. By our assumptions on
$\kappa $
and z. By our assumptions on
![]() $\kappa $
, there exists a transitive set M with
$\kappa $
, there exists a transitive set M with
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}\subseteq M\prec _{\Sigma _1}\mathrm {H}_{\kappa ^+}$
, a transitive set N with
$\mathrm {H}_{\kappa }\cup \{\kappa \}\subseteq M\prec _{\Sigma _1}\mathrm {H}_{\kappa ^+}$
, a transitive set N with
![]() $M\cup {}^{{<}\kappa }N\subseteq N$
, and a normal, weakly amenable N-ultrafilter F on
$M\cup {}^{{<}\kappa }N\subseteq N$
, and a normal, weakly amenable N-ultrafilter F on
![]() $\kappa $
with the property that
$\kappa $
with the property that
![]() $\langle N,\in ,F\rangle $
is iterable. This setup ensures that
$\langle N,\in ,F\rangle $
is iterable. This setup ensures that
![]() $E\in M$
and
$E\in M$
and
![]() $\varphi (E,\kappa ,z)$
holds in N. Moreover, the fact that E contains a closed unbounded subset of
$\varphi (E,\kappa ,z)$
holds in N. Moreover, the fact that E contains a closed unbounded subset of
![]() $\kappa $
implies that M contains such a subset of E and since F is a normal N-ultrafilter, we can conclude that E is an element of F. Pick an elementary submodel
$\kappa $
implies that M contains such a subset of E and since F is a normal N-ultrafilter, we can conclude that E is an element of F. Pick an elementary submodel
![]() $\langle X,\in ,F_0\rangle $
of
$\langle X,\in ,F_0\rangle $
of
![]() $\langle N,\in ,F\rangle $
of cardinality less than
$\langle N,\in ,F\rangle $
of cardinality less than
![]() $\kappa $
with
$\kappa $
with
![]() $\mathrm {{tc}}({\{z\}})\cup \{\kappa \}\subseteq X$
, and let
$\mathrm {{tc}}({\{z\}})\cup \{\kappa \}\subseteq X$
, and let
![]() ${\pi }:{X}\longrightarrow {N_0}$
denote the corresponding transitive collapse. Then,
${\pi }:{X}\longrightarrow {N_0}$
denote the corresponding transitive collapse. Then,
![]() $\pi (z)=z$
, and if we set
$\pi (z)=z$
, and if we set
![]() $U=\pi [F_0]$
, then U is a weakly amenable
$U=\pi [F_0]$
, then U is a weakly amenable
![]() $N_0$
-ultrafilter on
$N_0$
-ultrafilter on
![]() $\pi (\kappa )$
and [Reference Kanamori10, Theorem 19.15] ensures that
$\pi (\kappa )$
and [Reference Kanamori10, Theorem 19.15] ensures that
![]() $\langle N_0,\in ,U\rangle $
is iterable. Let
$\langle N_0,\in ,U\rangle $
is iterable. Let
denote the linear iteration of
![]() $\langle N_0,\in ,U\rangle $
. Then,
$\langle N_0,\in ,U\rangle $
. Then,
![]() $(j_{0,\kappa }\circ \pi )(\kappa )=\kappa $
,
$(j_{0,\kappa }\circ \pi )(\kappa )=\kappa $
,
![]() $(j_{0,\kappa }\circ \pi )(z)=z$
,
$(j_{0,\kappa }\circ \pi )(z)=z$
,
![]() $\Sigma _1$
-upwards absoluteness implies that
$\Sigma _1$
-upwards absoluteness implies that
![]() $\varphi ((j_{0,\kappa }\circ \pi )(E),\kappa ,z)$
holds in V, and hence, we know that
$\varphi ((j_{0,\kappa }\circ \pi )(E),\kappa ,z)$
holds in V, and hence, we know that
![]() $(j_{0,\kappa }\circ \pi )(E)=E$
. Moreover, the fact that
$(j_{0,\kappa }\circ \pi )(E)=E$
. Moreover, the fact that
![]() $E\in F$
ensures that
$E\in F$
ensures that
![]() $\pi (E)\in U$
and therefore
$\pi (E)\in U$
and therefore
![]() $(j_{0,\alpha }\circ \pi )(\kappa )\in (j_{0,\alpha +1}\circ \pi )(E)\subseteq E$
for all
$(j_{0,\alpha }\circ \pi )(\kappa )\in (j_{0,\alpha +1}\circ \pi )(E)\subseteq E$
for all
![]() $\alpha <\kappa $
. This shows that the closed unbounded subset
$\alpha <\kappa $
. This shows that the closed unbounded subset
![]() $C=\{{(j_{0,\alpha }\circ \pi )(\kappa )}~\vert ~{\alpha <\kappa }\}$
of
$C=\{{(j_{0,\alpha }\circ \pi )(\kappa )}~\vert ~{\alpha <\kappa }\}$
of
![]() $\kappa $
is a subset of E. Finally, the set
$\kappa $
is a subset of E. Finally, the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\kappa $
,
$\kappa $
,
![]() $N_0$
, and U.
$N_0$
, and U.
Proof of Theorem 4.1
The last two lemmata prove the first two assertions of the theorem. To prove the third assertion, let
![]() $\kappa $
be a stably measurable cardinal, let S be
$\kappa $
be a stably measurable cardinal, let S be
![]() $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
![]() $\kappa $
, and let
$\kappa $
, and let
![]() ${r}:{\kappa }\longrightarrow {\kappa }$
be a regressive function that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
be a regressive function that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Our earlier observations now show that there is a unique ordinal
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Our earlier observations now show that there is a unique ordinal
![]() $\alpha <\kappa $
with the property that the set
$\alpha <\kappa $
with the property that the set
![]() $r^{{-}1}\{\alpha \}$
contains a closed unbounded subset of
$r^{{-}1}\{\alpha \}$
contains a closed unbounded subset of
![]() $\kappa $
. Since the set
$\kappa $
. Since the set
![]() $\{r^{{-}1}\{\alpha \}\}$
is definable by a
$\{r^{{-}1}\{\alpha \}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
, Lemma 4.3 yields a closed unbounded subset C of
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
, Lemma 4.3 yields a closed unbounded subset C of
![]() $\kappa $
with
$\kappa $
with
![]() $C\subseteq r^{{-}1}\{\alpha \}$
and the property that the set
$C\subseteq r^{{-}1}\{\alpha \}$
and the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Then, r is constant on
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Then, r is constant on
![]() $C\cap S$
, and since
$C\cap S$
, and since
![]() $\kappa $
is an uncountable regular cardinal, we know that this set is
$\kappa $
is an uncountable regular cardinal, we know that this set is
![]() $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
![]() $\kappa $
.
$\kappa $
.
We can now show that in the Dodd–Jensen core model
![]() $\mathrm {{K}}^{DJ}$
, stably measurable cardinals are characterized by the
$\mathrm {{K}}^{DJ}$
, stably measurable cardinals are characterized by the
![]() $\boldsymbol {\Sigma }_1$
-stationarity of unbounded sets of cardinals:
$\boldsymbol {\Sigma }_1$
-stationarity of unbounded sets of cardinals:
Theorem 4.4 If
![]() $\mathrm {{V}}=\mathrm {{K}}^{DJ}$
, then the following statements are equivalent for every cardinal
$\mathrm {{V}}=\mathrm {{K}}^{DJ}$
, then the following statements are equivalent for every cardinal
![]() $\kappa>\omega _1$
:
$\kappa>\omega _1$
:
-
(1) The cardinal
 $\kappa $
is stably measurable.
$\kappa $
is stably measurable. -
(2) The set
 $\{\mathrm {H}_{\kappa }\}$
is not definable by a
$\{\mathrm {H}_{\kappa }\}$
is not definable by a
 $\Sigma _1$
-formula with parameters in the set
$\Sigma _1$
-formula with parameters in the set
 $\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. -
(3) The cardinal
 $\kappa $
is a limit cardinal, and every unbounded subset of
$\kappa $
is a limit cardinal, and every unbounded subset of
 $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
.
$\kappa $
.
Proof First, assume that
![]() $\kappa $
is not stably measurable. Then, we can apply [Reference Welch19, Theorem 2.6] to find a bistationary subset E of
$\kappa $
is not stably measurable. Then, we can apply [Reference Welch19, Theorem 2.6] to find a bistationary subset E of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{E\}$
is definable by a
$\{E\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Lemma 3.7 then shows that the set
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Lemma 3.7 then shows that the set
![]() $\{\mathrm {H}_{\kappa }\}$
is definable by a
$\{\mathrm {H}_{\kappa }\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
Now, assume that
![]() $\kappa $
is a limit cardinal and the set
$\kappa $
is a limit cardinal and the set
![]() $\{\mathrm {H}_{\kappa }\}$
is definable by a
$\{\mathrm {H}_{\kappa }\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Let C denote the set of all limit cardinals smaller than
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Let C denote the set of all limit cardinals smaller than
![]() $\kappa $
. Our assumption then implies that the set
$\kappa $
. Our assumption then implies that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. If C is unbounded in
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. If C is unbounded in
![]() $\kappa $
, then the set of all successor cardinals smaller than
$\kappa $
, then the set of all successor cardinals smaller than
![]() $\kappa $
is an unbounded subset of
$\kappa $
is an unbounded subset of
![]() $\kappa $
that consists of cardinals and is not
$\kappa $
that consists of cardinals and is not
![]() $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
![]() $\kappa $
. In the other case, if C is bounded in
$\kappa $
. In the other case, if C is bounded in
![]() $\kappa $
, then
$\kappa $
, then
![]() ${\mathrm {{cof}}(\kappa )}=\omega $
, Lemma 3.3 yields a cofinal function
${\mathrm {{cof}}(\kappa )}=\omega $
, Lemma 3.3 yields a cofinal function
![]() ${c}:{\omega }\longrightarrow {\kappa }$
that is definable by a
${c}:{\omega }\longrightarrow {\kappa }$
that is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
, and the set
$\kappa $
, and the set
![]() $D=\{{c(n)+1}~\vert ~{n<\omega }\}$
is closed unbounded in
$D=\{{c(n)+1}~\vert ~{n<\omega }\}$
is closed unbounded in
![]() $\kappa $
that contains no cardinals and has the property that the set
$\kappa $
that contains no cardinals and has the property that the set
![]() $\{D\}$
is definable by a
$\{D\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
.
$\kappa $
.
Together with Theorem 4.1, these computations establish all equivalences claimed in the theorem.
Next, we show that stable measurability provides the exact consistency strength for the existence of limit cardinals with given undefinability property:
Theorem 4.5 The following statements are equiconsistent over
![]() $\mathrm {{ZFC}}$
:
$\mathrm {{ZFC}}$
:
-
(1) There exists a stably measurable cardinal.
-
(2) There exists a limit cardinal
 $\kappa $
with the property that every unbounded subset of
$\kappa $
with the property that every unbounded subset of
 $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
.
$\kappa $
.
Proof Assume, toward a contradiction, that there is no inner model with a stably measurable cardinal and
![]() $\kappa $
is a limit cardinal with the property that every unbounded subset of
$\kappa $
is a limit cardinal with the property that every unbounded subset of
![]() $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
![]() $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
![]() $\kappa $
. Then, Corollary 3.5 shows that
$\kappa $
. Then, Corollary 3.5 shows that
![]() $\kappa $
is regular. Since
$\kappa $
is regular. Since
![]() $\kappa $
is not stably measurable in
$\kappa $
is not stably measurable in
![]() $\mathrm {{K}}^{DJ}$
, Theorem 4.4 now shows that in
$\mathrm {{K}}^{DJ}$
, Theorem 4.4 now shows that in
![]() $\mathrm {K}^{DJ}$
, the set
$\mathrm {K}^{DJ}$
, the set
![]() $\{\mathrm {H}_{\kappa }\}$
is definable by a
$\{\mathrm {H}_{\kappa }\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Let C denote the set of all ordinals less than
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Let C denote the set of all ordinals less than
![]() $\kappa $
that are limit cardinals in
$\kappa $
that are limit cardinals in
![]() $\mathrm {{K}}^{DJ}$
. Then, C is a closed unbounded subset of
$\mathrm {{K}}^{DJ}$
. Then, C is a closed unbounded subset of
![]() $\kappa $
, and since the class
$\kappa $
, and since the class
![]() $\mathrm {{K}}^{DJ}$
is definable by a
$\mathrm {{K}}^{DJ}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
, the set
$\kappa $
, the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Now, let E denote the set of all successor cardinals of singular cardinals less than
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Now, let E denote the set of all successor cardinals of singular cardinals less than
![]() $\kappa $
. The results of [Reference Dodd and Jensen4] then show that the elements of E are successor cardinals of singular cardinals in
$\kappa $
. The results of [Reference Dodd and Jensen4] then show that the elements of E are successor cardinals of singular cardinals in
![]() $\mathrm {{K}}^{DJ}$
, and hence,
$\mathrm {{K}}^{DJ}$
, and hence,
![]() $C\cap E=\emptyset $
. This shows that E is an unbounded subset of
$C\cap E=\emptyset $
. This shows that E is an unbounded subset of
![]() $\kappa $
that consists of cardinals and is not
$\kappa $
that consists of cardinals and is not
![]() $\boldsymbol {\Sigma }_1$
-stationary. In combination with Theorem 4.1, these arguments prove the desired equivalence.
$\boldsymbol {\Sigma }_1$
-stationary. In combination with Theorem 4.1, these arguments prove the desired equivalence.
In Section 5, we show that the assertion in item (2) of the last theorem can consistently hold at
![]() $\kappa = \aleph _\omega $
, starting from the consistency assumption of a measurable cardinal.
$\kappa = \aleph _\omega $
, starting from the consistency assumption of a measurable cardinal.
4.2 Limits of measurable cardinals
We now continue by showing that many of the above results can be extended to larger classes of definable sets if the given cardinal is a (not necessarily regular) limit of measurable cardinals:
Theorem 4.6 Let
![]() $\kappa $
be a cardinal that is a limit of measurable cardinals.
$\kappa $
be a cardinal that is a limit of measurable cardinals.
-
(1) Every unbounded subset S of
 $\kappa $
consisting of cardinals is
$\kappa $
consisting of cardinals is
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary.
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary. -
(2) If S is a
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of
 $\kappa $
and
$\kappa $
and
 ${r}:{\kappa }\longrightarrow {\kappa }$
is a regressive function that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
is a regressive function that is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 $\mathrm {H}_{\kappa }\cup \mathrm{Ord}$
, then r is constant on a
$\mathrm {H}_{\kappa }\cup \mathrm{Ord}$
, then r is constant on a
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of S.
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of S.
The starting point of the proof of this theorem is the following technical lemma that generalizes [Reference Larson13, Lemma 1.1.25] to embeddings given by linear iterations.
Lemma 4.7 Suppose that
![]() $\kappa _0<\kappa _1$
are measurable cardinals and
$\kappa _0<\kappa _1$
are measurable cardinals and
![]() $\alpha _0 < \kappa _1$
is an ordinal. Given
$\alpha _0 < \kappa _1$
is an ordinal. Given
![]() $i<2$
, let
$i<2$
, let
![]() $U_i$
be a normal ultrafilter on
$U_i$
be a normal ultrafilter on
![]() $\kappa _i$
, and let
$\kappa _i$
, and let
denote the linear iteration of
![]() $\langle \mathrm {{V}},\in ,U_i\rangle $
. In addition, let
$\langle \mathrm {{V}},\in ,U_i\rangle $
. In addition, let
denote the linear iteration of
![]() $\langle M^0_{\alpha _0},\in ,j^0_{0,\alpha _0}(U_1)\rangle $
. Then,
$\langle M^0_{\alpha _0},\in ,j^0_{0,\alpha _0}(U_1)\rangle $
. Then,
![]() $j^*_{0,\alpha }\restriction \mathrm{Ord}=j^1_{0,\alpha }\restriction \mathrm{Ord}$
for all
$j^*_{0,\alpha }\restriction \mathrm{Ord}=j^1_{0,\alpha }\restriction \mathrm{Ord}$
for all
![]() $\alpha \in \mathrm{Ord}$
.
$\alpha \in \mathrm{Ord}$
.
Proof Fix an ordinal
![]() $\alpha _1<\kappa $
with the property that
$\alpha _1<\kappa $
with the property that
![]() $j^*_{0,\alpha }\restriction \mathrm{Ord}=j^1_{0,\alpha }\restriction \mathrm{Ord}$
holds for all
$j^*_{0,\alpha }\restriction \mathrm{Ord}=j^1_{0,\alpha }\restriction \mathrm{Ord}$
holds for all
![]() $\alpha <\alpha _1$
. Set
$\alpha <\alpha _1$
. Set
![]() $M^0=M^0_{\alpha _0}$
,
$M^0=M^0_{\alpha _0}$
,
![]() $M^1=M^1_{\alpha _1}$
,
$M^1=M^1_{\alpha _1}$
,
![]() $M^*=M^*_{\alpha _1}$
,
$M^*=M^*_{\alpha _1}$
,
![]() $j^0=j^0_{0,\alpha _0}$
,
$j^0=j^0_{0,\alpha _0}$
,
![]() $j^1=j^1_{0,\alpha _1}$
,
$j^1=j^1_{0,\alpha _1}$
,
![]() $j^*=j^*_{0,\alpha _1}$
, and
$j^*=j^*_{0,\alpha _1}$
, and
![]() $U_*=j^0(U_1)$
. Then,
$U_*=j^0(U_1)$
. Then,
![]() $j^0(\kappa _1)=\kappa _1$
. In addition, if
$j^0(\kappa _1)=\kappa _1$
. In addition, if
![]() $i<2$
, then we define
$i<2$
, then we define
![]() $\kappa ^i_\alpha =j^i_{0,\alpha }(\kappa _i)$
for all
$\kappa ^i_\alpha =j^i_{0,\alpha }(\kappa _i)$
for all
![]() $\alpha \in \mathrm{Ord}$
and
$\alpha \in \mathrm{Ord}$
and
![]() $C^i=\{{\kappa ^i_\alpha }~\vert ~{\alpha <\alpha _i}\}$
. An application of [Reference Kanamori10, Lemma 19.6] then shows that every element of
$C^i=\{{\kappa ^i_\alpha }~\vert ~{\alpha <\alpha _i}\}$
. An application of [Reference Kanamori10, Lemma 19.6] then shows that every element of
![]() $M^*$
is of the form
$M^*$
is of the form
![]() $j^0(f)(c)$
with
$j^0(f)(c)$
with
![]() $n<\omega $
,
$n<\omega $
,
![]() ${f}:{[\kappa _0]^n}\longrightarrow {V}$
and
${f}:{[\kappa _0]^n}\longrightarrow {V}$
and
![]() $c\in [C^0]^n$
. In addition, given
$c\in [C^0]^n$
. In addition, given
![]() $i<2$
and
$i<2$
and
![]() $n<\omega $
, we define
$n<\omega $
, we define
The results of [Reference Kanamori10, Chapter 19] then show that
![]() $U_i^n$
is a
$U_i^n$
is a
![]() ${<}\kappa _i$
-complete ultrafilter on
${<}\kappa _i$
-complete ultrafilter on
![]() $[\kappa _i]^n$
. Set
$[\kappa _i]^n$
. Set
![]() $U_*^n=j^0(U_1^n)$
for all
$U_*^n=j^0(U_1^n)$
for all
![]() $n<\omega $
. Our assumption now implies that
$n<\omega $
. Our assumption now implies that
![]() $j^*_{0,\alpha }(\kappa _1)=\kappa ^1_\alpha $
holds for all
$j^*_{0,\alpha }(\kappa _1)=\kappa ^1_\alpha $
holds for all
![]() $\alpha <\alpha _1$
. In particular, we know that every ordinal is of the form
$\alpha <\alpha _1$
. In particular, we know that every ordinal is of the form
![]() $j^*(g)(d)$
with
$j^*(g)(d)$
with
![]() $n<\omega $
,
$n<\omega $
,
![]() ${g}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in
${g}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in
![]() $M_0$
and
$M_0$
and
![]() $d\in [C^1]^n$
.
$d\in [C^1]^n$
.
Claim If
![]() $n<\omega $
,
$n<\omega $
,
![]() $B\in U_1^n$
, and
$B\in U_1^n$
, and
![]() $B_*\in U_*^n$
, then
$B_*\in U_*^n$
, then
![]() $j^0[B]\cap B_*\neq \emptyset $
.
$j^0[B]\cap B_*\neq \emptyset $
.
Proof of the Claim
Pick
![]() $n<\omega $
,
$n<\omega $
,
![]() ${f}:{[\kappa _0]^n}\longrightarrow {V}$
and
${f}:{[\kappa _0]^n}\longrightarrow {V}$
and
![]() $c\in [C^0]^n$
with
$c\in [C^0]^n$
with
![]() $B_*=j^0(f)(c)$
. By [Reference Kanamori10, Lemma 19.9], we then have
$B_*=j^0(f)(c)$
. By [Reference Kanamori10, Lemma 19.9], we then have
Since
![]() $U_0^n$
has cardinality less than
$U_0^n$
has cardinality less than
![]() $\kappa _1$
, the
$\kappa _1$
, the
![]() ${<}\kappa _1$
-completeness of
${<}\kappa _1$
-completeness of
![]() $U_1^n$
implies that
$U_1^n$
implies that
![]() $E=\bigcap \{{f(a)}~\vert ~{a\in D}\}$
is an element of
$E=\bigcap \{{f(a)}~\vert ~{a\in D}\}$
is an element of
![]() $U_1^n$
. Pick
$U_1^n$
. Pick
![]() $b\in B\cap E$
. Then,
$b\in B\cap E$
. Then,
and [Reference Kanamori10, Lemma 19.9] shows that
![]() $j^0(b)\in j^0[B]\cap j^0(f)(c)=j^0[B]\cap B_*\neq \emptyset $
.
$j^0(b)\in j^0[B]\cap j^0(f)(c)=j^0[B]\cap B_*\neq \emptyset $
.
Claim If
![]() $n<\omega $
and
$n<\omega $
and
![]() ${g_0,g_1}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
are functions in
${g_0,g_1}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
are functions in
![]() $M^0$
with
$M^0$
with
then
Proof of the Claim
Assume, toward a contradiction, that the above conclusion fails. Then, we know that the set
![]() $B=\{{b\in [\kappa _1]^n}~\vert ~{g_0(j^0(b))\neq g_1(j^0(b))}\}$
is an element of
$B=\{{b\in [\kappa _1]^n}~\vert ~{g_0(j^0(b))\neq g_1(j^0(b))}\}$
is an element of
![]() $U_1^n$
. In this situation, we can use our first claim to find
$U_1^n$
. In this situation, we can use our first claim to find
![]() $b\in B$
with
$b\in B$
with
![]() $g_0(j^0(b))=g_1(j^0(b))$
, a contradiction.
$g_0(j^0(b))=g_1(j^0(b))$
, a contradiction.
The same proof also yields the following implication:
Claim If
![]() $n<\omega $
and
$n<\omega $
and
![]() ${g_0,g_1}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
are functions in
${g_0,g_1}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
are functions in
![]() $M^0$
such that the set
$M^0$
such that the set
![]() $\{{b\in [\kappa _1]^n}~\vert ~{g_0(b)<g_1(b)}\}$
is an element of
$\{{b\in [\kappa _1]^n}~\vert ~{g_0(b)<g_1(b)}\}$
is an element of
![]() $U_*^n$
, then the set
$U_*^n$
, then the set
is an element of
![]() $U_1^n$
.
$U_1^n$
.
Claim For every function
![]() ${f}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in V, there is a function
${f}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in V, there is a function
![]() ${g}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in
${g}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in
![]() $M^0$
with
$M^0$
with
Proof of the Claim
Given
![]() $b\in [\kappa _1]^n$
, pick
$b\in [\kappa _1]^n$
, pick
![]() $m_b<\omega $
,
$m_b<\omega $
,
![]() ${f_b}:{[\kappa _0]^{m_b}}\longrightarrow {\mathrm{Ord}}$
in V and
${f_b}:{[\kappa _0]^{m_b}}\longrightarrow {\mathrm{Ord}}$
in V and
![]() $c_b\in [C^0]^{m_b}$
with
$c_b\in [C^0]^{m_b}$
with
![]() $f(b)=j^0(f_b)(c_b)$
. Then, there is
$f(b)=j^0(f_b)(c_b)$
. Then, there is
![]() $m<\omega $
and
$m<\omega $
and
![]() $c\in [C^0]^m$
with
$c\in [C^0]^m$
with
Define
and
Then, g is an element of
![]() $M^0$
, and
$M^0$
, and
holds for all
![]() $b\in B\in U_1^n$
.
$b\in B\in U_1^n$
.
Claim If
![]() ${g}:{[\kappa _1]^1}\longrightarrow {\mathrm{Ord}}$
is an element of
${g}:{[\kappa _1]^1}\longrightarrow {\mathrm{Ord}}$
is an element of
![]() $M^0$
, then
$M^0$
, then
Proof of the Claim
Since standard arguments show that
![]() $\{{\{\gamma \}}~\vert ~{\gamma <\kappa _1, j^0(\gamma )=\gamma }\}$
is an element of
$\{{\{\gamma \}}~\vert ~{\gamma <\kappa _1, j^0(\gamma )=\gamma }\}$
is an element of
![]() $U^1_1$
, we know that the set
$U^1_1$
, we know that the set
![]() $\{{\{\gamma \}}~\vert ~{\gamma <\kappa _1, (g\circ j^0)(\gamma )=g(\gamma )}\}$
is also contained in
$\{{\{\gamma \}}~\vert ~{\gamma <\kappa _1, (g\circ j^0)(\gamma )=g(\gamma )}\}$
is also contained in
![]() $U_1^1$
, and hence, an application of [Reference Kanamori10, Lemma 19.9] shows that we have
$U_1^1$
, and hence, an application of [Reference Kanamori10, Lemma 19.9] shows that we have
![]() $j^1(g\circ j^0)(\{\kappa _1\}) = j^1(g)(\{\kappa _1\})$
.
$j^1(g\circ j^0)(\{\kappa _1\}) = j^1(g)(\{\kappa _1\})$
.
By our second claim and [Reference Kanamori10, Lemma 19.9], there exists a well-defined class function
![]() ${F}:{\mathrm{Ord}}\longrightarrow {\mathrm{Ord}}$
with the property that
${F}:{\mathrm{Ord}}\longrightarrow {\mathrm{Ord}}$
with the property that
holds for all
![]() $n<\omega $
,
$n<\omega $
,
![]() ${g}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in
${g}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in
![]() $M^0$
and
$M^0$
and
![]() $c\in [C^1]^n$
. Moreover, our third claim shows that F is order-preserving. Finally, since every ordinal is of the form
$c\in [C^1]^n$
. Moreover, our third claim shows that F is order-preserving. Finally, since every ordinal is of the form
![]() $j^1(f)(c)$
for some
$j^1(f)(c)$
for some
![]() $n<\omega $
,
$n<\omega $
,
![]() ${f}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in V and
${f}:{[\kappa _1]^n}\longrightarrow {\mathrm{Ord}}$
in V and
![]() $c\in [C^1]^n$
, our fourth claim shows that F is also surjective. In combination, this shows that F is the identity on
$c\in [C^1]^n$
, our fourth claim shows that F is also surjective. In combination, this shows that F is the identity on
![]() $\mathrm{Ord}$
. Now, fix an ordinal
$\mathrm{Ord}$
. Now, fix an ordinal
![]() $\gamma $
, and let
$\gamma $
, and let
![]() $g_\gamma $
denote the constant function on
$g_\gamma $
denote the constant function on
![]() $[\kappa _1]^1$
with value
$[\kappa _1]^1$
with value
![]() $\gamma $
. Then, we have
$\gamma $
. Then, we have
 $$ \begin{align*} \begin{aligned} j^*(\gamma) ~ & = ~ j^*(g_\gamma)(\{\kappa_1\}) ~ = ~ F(j^*(g_\gamma)(\{\kappa_1\})) \\ & = ~ j^1(g_\gamma\circ j^0)(\{\kappa_1\}) ~ = ~ j^1(g_\gamma)(\{\kappa_1\}) ~ = ~ j^1(\gamma), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} j^*(\gamma) ~ & = ~ j^*(g_\gamma)(\{\kappa_1\}) ~ = ~ F(j^*(g_\gamma)(\{\kappa_1\})) \\ & = ~ j^1(g_\gamma\circ j^0)(\{\kappa_1\}) ~ = ~ j^1(g_\gamma)(\{\kappa_1\}) ~ = ~ j^1(\gamma), \end{aligned} \end{align*} $$
and this proves the statement of the lemma.
Using the above results, we can now drive a variation of [Reference Larson13, Lemma 1.1.27] for iterations. The following lemma will be the main tool used in the proofs of this section.
Lemma 4.8 Let
![]() $\lambda \geq \aleph _0$
be a regular cardinal, let
$\lambda \geq \aleph _0$
be a regular cardinal, let
![]() $\vec {\kappa }=\langle {\kappa _\xi }~\vert ~{\xi <\lambda }\rangle $
be a strictly increasing sequence of measurable cardinals with supremum
$\vec {\kappa }=\langle {\kappa _\xi }~\vert ~{\xi <\lambda }\rangle $
be a strictly increasing sequence of measurable cardinals with supremum
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $\vec {U}=\langle {U_\xi }~\vert ~{\xi <\lambda }\rangle $
be a sequence with the property that
$\vec {U}=\langle {U_\xi }~\vert ~{\xi <\lambda }\rangle $
be a sequence with the property that
![]() $U_\xi $
is a normal ultrafilter on
$U_\xi $
is a normal ultrafilter on
![]() $\kappa _\xi $
for all
$\kappa _\xi $
for all
![]() $\xi <\lambda $
. Assume that either
$\xi <\lambda $
. Assume that either
![]() $\kappa =\lambda $
or
$\kappa =\lambda $
or
![]() $\lambda <\kappa _0$
. Given
$\lambda <\kappa _0$
. Given
![]() $\xi <\lambda $
, let
$\xi <\lambda $
, let
denote the linear iteration of
![]() $\langle \mathrm {{V}},\in ,U_\xi \rangle $
. Then, for all ordinals
$\langle \mathrm {{V}},\in ,U_\xi \rangle $
. Then, for all ordinals
![]() $\gamma $
and eventually all
$\gamma $
and eventually all
![]() $\xi <\lambda $
, we have
$\xi <\lambda $
, we have
![]() $j^\xi _{0,\alpha }(\gamma )=\gamma $
for all
$j^\xi _{0,\alpha }(\gamma )=\gamma $
for all
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
Proof Assume, toward a contradiction, that there is an ordinal
![]() $\gamma $
such that for unboundedly many
$\gamma $
such that for unboundedly many
![]() $\xi <\lambda $
, there is an
$\xi <\lambda $
, there is an
![]() $\alpha <\kappa $
with
$\alpha <\kappa $
with
![]() $j^\xi _{0,\alpha }(\gamma )>\gamma $
. Let
$j^\xi _{0,\alpha }(\gamma )>\gamma $
. Let
![]() $\gamma $
be minimal with this property. Pick
$\gamma $
be minimal with this property. Pick
![]() $\zeta <\lambda $
and
$\zeta <\lambda $
and
![]() $\alpha _0<\kappa $
with
$\alpha _0<\kappa $
with
![]() $j^\zeta _{0,\alpha _0}(\gamma )>\gamma $
. Set
$j^\zeta _{0,\alpha _0}(\gamma )>\gamma $
. Set
![]() $j=j^\zeta _{0,\alpha _0}$
and
$j=j^\zeta _{0,\alpha _0}$
and
![]() $M=M^\zeta _{\alpha _0}$
. Then,
$M=M^\zeta _{\alpha _0}$
. Then,
![]() $j(\lambda )=\lambda $
and
$j(\lambda )=\lambda $
and
![]() $j(\kappa )=\kappa $
. Moreover, if we set
$j(\kappa )=\kappa $
. Moreover, if we set
![]() $j(\vec {\kappa })=\langle {\kappa ^\prime _\xi }~\vert ~{\xi <\lambda }\rangle $
and
$j(\vec {\kappa })=\langle {\kappa ^\prime _\xi }~\vert ~{\xi <\lambda }\rangle $
and
![]() $j(\vec {U})=\langle {U^\prime _\xi }~\vert ~{\xi <\lambda }\rangle $
, then the fact that
$j(\vec {U})=\langle {U^\prime _\xi }~\vert ~{\xi <\lambda }\rangle $
, then the fact that
![]() $j(\gamma )>\gamma $
yields an ordinal
$j(\gamma )>\gamma $
yields an ordinal
![]() $\rho <\lambda $
with the property that
$\rho <\lambda $
with the property that
![]() $i^\xi _{0,\alpha }(\gamma )=\gamma $
holds for all
$i^\xi _{0,\alpha }(\gamma )=\gamma $
holds for all
![]() $\rho \leq \xi <\lambda $
and all
$\rho \leq \xi <\lambda $
and all
![]() $\alpha <\kappa $
, where
$\alpha <\kappa $
, where
denotes the linear iteration of
![]() $\langle M,\in ,U^\prime _\xi \rangle $
. By our assumption, we are now able to pick
$\langle M,\in ,U^\prime _\xi \rangle $
. By our assumption, we are now able to pick
![]() $\rho <\xi <\lambda $
and
$\rho <\xi <\lambda $
and
![]() $\alpha _1<\kappa $
such that
$\alpha _1<\kappa $
such that
![]() $\kappa _\xi>\alpha _0$
and
$\kappa _\xi>\alpha _0$
and
![]() $j^\xi _{0,\alpha _1}(\gamma )>\gamma $
. In this situation, Lemma 4.7 implies that
$j^\xi _{0,\alpha _1}(\gamma )>\gamma $
. In this situation, Lemma 4.7 implies that
![]() $i^{j(\xi )}_{0,\alpha _1}(\gamma )=j^\xi _{0,\alpha _1}(\gamma )>\gamma $
, and since
$i^{j(\xi )}_{0,\alpha _1}(\gamma )=j^\xi _{0,\alpha _1}(\gamma )>\gamma $
, and since
![]() $\rho \leq \xi \leq j(\xi )<\lambda $
, this yields a contradiction.
$\rho \leq \xi \leq j(\xi )<\lambda $
, this yields a contradiction.
With the help of Lemma 4.8, we can now work toward a proof of the first part of Theorem 4.6.
Lemma 4.9 In the setting of Lemma 4.8, for every ordinal
![]() $\gamma \geq \kappa $
, there exists an ordinal
$\gamma \geq \kappa $
, there exists an ordinal
![]() $\lambda _0<\lambda $
with the property that the cardinal
$\lambda _0<\lambda $
with the property that the cardinal
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _1(\kappa _\xi ,\gamma )$
-undefinability property for all
$\Sigma _1(\kappa _\xi ,\gamma )$
-undefinability property for all
![]() $\lambda _0\leq \xi <\lambda $
.
$\lambda _0\leq \xi <\lambda $
.
Proof Lemma 4.8 yields
![]() $\lambda _0<\lambda $
with the property that
$\lambda _0<\lambda $
with the property that
![]() $j^\xi _{0,\alpha }(\kappa )=\kappa $
and
$j^\xi _{0,\alpha }(\kappa )=\kappa $
and
![]() $j^\xi _{0,\alpha }(\gamma )=\gamma $
holds for all
$j^\xi _{0,\alpha }(\gamma )=\gamma $
holds for all
![]() $\lambda _0\leq \xi <\lambda $
and
$\lambda _0\leq \xi <\lambda $
and
![]() $\alpha <\kappa $
. Assume, toward a contradiction, that there is a
$\alpha <\kappa $
. Assume, toward a contradiction, that there is a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
, and ordinal
$\varphi (v_0,\ldots ,v_3)$
, and ordinal
![]() $\lambda _0\leq \xi <\lambda $
, an element z of
$\lambda _0\leq \xi <\lambda $
, an element z of
![]() $\mathrm {H}_{\kappa _\xi }$
, and an ordinal
$\mathrm {H}_{\kappa _\xi }$
, and an ordinal
![]() $\alpha $
in the interval
$\alpha $
in the interval
![]() $[\kappa _\xi ,\kappa )$
such that the set
$[\kappa _\xi ,\kappa )$
such that the set
![]() $\{\alpha \}$
is definable by the formula
$\{\alpha \}$
is definable by the formula
![]() $\varphi (v_0,\ldots ,v_3)$
and the parameters
$\varphi (v_0,\ldots ,v_3)$
and the parameters
![]() $\kappa $
,
$\kappa $
,
![]() $\gamma $
, and z. Pick an ordinal
$\gamma $
, and z. Pick an ordinal
![]() $\beta <\kappa $
with
$\beta <\kappa $
with
![]() $j^\xi _{0,\beta }(\kappa _\xi )>\alpha $
. Then, we know that
$j^\xi _{0,\beta }(\kappa _\xi )>\alpha $
. Then, we know that
![]() $j^\xi _{0,\beta }(\alpha )>\alpha $
, and elementarity implies that
$j^\xi _{0,\beta }(\alpha )>\alpha $
, and elementarity implies that
![]() $\varphi (j^\xi _{0,\beta }(\alpha ),\kappa ,\gamma ,z)$
holds in
$\varphi (j^\xi _{0,\beta }(\alpha ),\kappa ,\gamma ,z)$
holds in
![]() $M^\xi _\beta $
. But then,
$M^\xi _\beta $
. But then,
![]() $\Sigma _1$
-upwards absoluteness implies that
$\Sigma _1$
-upwards absoluteness implies that
![]() $\varphi (j^\xi _{0,\beta }(\alpha ),\kappa ,\gamma ,z)$
holds in V, contradicting our assumptions.
$\varphi (j^\xi _{0,\beta }(\alpha ),\kappa ,\gamma ,z)$
holds in V, contradicting our assumptions.
Lemma 4.10 Let
![]() $\kappa $
be a cardinal that is a limit of measurable cardinals. Then, every unbounded subset of
$\kappa $
be a cardinal that is a limit of measurable cardinals. Then, every unbounded subset of
![]() $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
![]() $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
![]() $\kappa $
.
$\kappa $
.
Proof Work in the setting of Lemma 4.8. Let E be an unbounded subset of
![]() $\kappa $
that consists of cardinals, and fix a
$\kappa $
that consists of cardinals, and fix a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
, an ordinal
$\varphi (v_0,v_1,v_2)$
, an ordinal
![]() $\gamma $
, and
$\gamma $
, and
![]() $z\in \mathrm {H}_{\kappa }$
with the property that there exists a closed unbounded subset C of
$z\in \mathrm {H}_{\kappa }$
with the property that there exists a closed unbounded subset C of
![]() $\kappa $
that is the unique set x with the property that
$\kappa $
that is the unique set x with the property that
![]() $\varphi (x,\gamma ,z)$
holds. By combining Lemma 4.8 and Lemma 4.9 with Corollary 2.13, we can find
$\varphi (x,\gamma ,z)$
holds. By combining Lemma 4.8 and Lemma 4.9 with Corollary 2.13, we can find
![]() $\xi <\lambda $
such that
$\xi <\lambda $
such that
![]() $\kappa _\xi $
is an element of C,
$\kappa _\xi $
is an element of C,
![]() $z\in \mathrm {H}_{\kappa _\xi }$
, and for all
$z\in \mathrm {H}_{\kappa _\xi }$
, and for all
![]() $\alpha <\kappa $
, we have
$\alpha <\kappa $
, we have
![]() $j^\xi _{0,\alpha }(\kappa )=\kappa $
and
$j^\xi _{0,\alpha }(\kappa )=\kappa $
and
![]() $j^\xi _{0,\alpha }(\gamma )=\gamma $
. In this situation, we can find a cardinal
$j^\xi _{0,\alpha }(\gamma )=\gamma $
. In this situation, we can find a cardinal
![]() $\kappa _\xi <\mu \in E$
with
$\kappa _\xi <\mu \in E$
with
![]() $j^\xi _{0,\mu }(\kappa _\xi )=\mu $
. Then,
$j^\xi _{0,\mu }(\kappa _\xi )=\mu $
. Then,
![]() $\varphi (j^\xi _{0,\mu }(C),\gamma ,z)$
holds in
$\varphi (j^\xi _{0,\mu }(C),\gamma ,z)$
holds in
![]() $M^\xi _\mu $
, and since
$M^\xi _\mu $
, and since
![]() $\Sigma _1$
-upwards absoluteness implies that this statement also holds in
$\Sigma _1$
-upwards absoluteness implies that this statement also holds in
![]() $\mathrm {{V}}$
, it follows that
$\mathrm {{V}}$
, it follows that
![]() $j^\xi _{0,\mu }(C)=C$
. Moreover, since
$j^\xi _{0,\mu }(C)=C$
. Moreover, since
![]() $\kappa _\xi \in C$
, we can now use elementarity to conclude that
$\kappa _\xi \in C$
, we can now use elementarity to conclude that
![]() $\mu =j^\xi _{0,\mu }(\kappa _\xi )\in C\cap E\neq \emptyset $
.
$\mu =j^\xi _{0,\mu }(\kappa _\xi )\in C\cap E\neq \emptyset $
.
The next result generalizes [Reference Welch19, Theorem 1.26] and Lemma 4.3 to (possibly singular) limits of singular cardinals:
Lemma 4.11 Let
![]() $\kappa $
be a cardinal that is a limit of measurable cardinals, and let E be a subset of
$\kappa $
be a cardinal that is a limit of measurable cardinals, and let E be a subset of
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{E\}$
is definable by a
$\{E\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm{Ord}\cup \mathrm {H}_{\kappa }$
. Then, there exists a closed unbounded subset C of
$\mathrm{Ord}\cup \mathrm {H}_{\kappa }$
. Then, there exists a closed unbounded subset C of
![]() $\kappa $
of order type
$\kappa $
of order type
![]() $\kappa $
with the property that the set
$\kappa $
with the property that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
, and either
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
, and either
![]() $C\subseteq E$
or
$C\subseteq E$
or
![]() $C\cap E=\emptyset $
holds.
$C\cap E=\emptyset $
holds.
Proof We may assume that there is a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
, an ordinal
$\varphi (v_0,v_1,v_2)$
, an ordinal
![]() $\gamma $
, and
$\gamma $
, and
![]() $z\in \mathrm {H}_{\kappa }$
with the property that E is the unique set x satisfying
$z\in \mathrm {H}_{\kappa }$
with the property that E is the unique set x satisfying
![]() $\varphi (x,\gamma ,z)$
. By Lemma 4.8, there exists a measurable cardinal
$\varphi (x,\gamma ,z)$
. By Lemma 4.8, there exists a measurable cardinal
![]() $\kappa _0<\kappa $
with
$\kappa _0<\kappa $
with
![]() $z\in \mathrm {H}_{\kappa _0}$
and a normal ultrafilter U on
$z\in \mathrm {H}_{\kappa _0}$
and a normal ultrafilter U on
![]() $\kappa _0$
satisfying
$\kappa _0$
satisfying
![]() $j_{0,\alpha }(\kappa )=\kappa $
and
$j_{0,\alpha }(\kappa )=\kappa $
and
![]() $j_{0,\alpha }(\gamma )=\gamma $
for all
$j_{0,\alpha }(\gamma )=\gamma $
for all
![]() $\alpha <\kappa $
, where
$\alpha <\kappa $
, where
is the linear iteration of
![]() $\langle V,\in ,U\rangle $
. Given an ordinal
$\langle V,\in ,U\rangle $
. Given an ordinal
![]() $\alpha <\kappa $
, elementarity ensures that
$\alpha <\kappa $
, elementarity ensures that
![]() $\varphi (j_{0,\alpha }(E),\gamma ,z)$
holds in
$\varphi (j_{0,\alpha }(E),\gamma ,z)$
holds in
![]() $M_\alpha $
. In this situation,
$M_\alpha $
. In this situation,
![]() $\Sigma _1$
-upwards absoluteness implies that
$\Sigma _1$
-upwards absoluteness implies that
![]() $\varphi (j_{0,\alpha }(E),\gamma ,z)$
holds in V for all
$\varphi (j_{0,\alpha }(E),\gamma ,z)$
holds in V for all
![]() $\alpha <\kappa $
, and this allows us to conclude that
$\alpha <\kappa $
, and this allows us to conclude that
![]() $j_{0,\alpha }(E)=E$
holds for all
$j_{0,\alpha }(E)=E$
holds for all
![]() $\alpha <\kappa $
. If
$\alpha <\kappa $
. If
![]() $\kappa _0$
is an element of E, then these observations show that
$\kappa _0$
is an element of E, then these observations show that
![]() $\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}$
is a closed unbounded subset of E of order type
$\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}$
is a closed unbounded subset of E of order type
![]() $\kappa $
. In the other case, if
$\kappa $
. In the other case, if
![]() $\kappa _0\notin E$
, then
$\kappa _0\notin E$
, then
![]() $\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}$
is a closed unbounded subset of E of order type
$\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}$
is a closed unbounded subset of E of order type
![]() $\kappa $
that is disjoint from E.
$\kappa $
that is disjoint from E.
Now, pick a transitive model N of
![]() $\mathrm {{ZFC}}^-$
such that N contains
$\mathrm {{ZFC}}^-$
such that N contains
![]() $\kappa $
and U and the model
$\kappa $
and U and the model
![]() $\langle N,\in ,U\rangle $
is linearly iterable. Let
$\langle N,\in ,U\rangle $
is linearly iterable. Let
denote the linear iteration of
![]() $\langle N,\in ,U\rangle $
. In this situation, the fact that
$\langle N,\in ,U\rangle $
. In this situation, the fact that
![]() ${\mathcal {P}}({\kappa _0})\subseteq N$
implies that
${\mathcal {P}}({\kappa _0})\subseteq N$
implies that
![]() $j_{0,\alpha }(\kappa _0)=i_{0,\alpha }(\kappa _0)$
holds for all
$j_{0,\alpha }(\kappa _0)=i_{0,\alpha }(\kappa _0)$
holds for all
![]() $\alpha <\kappa $
. Since the class of all sets N with the above properties is definable by a
$\alpha <\kappa $
. Since the class of all sets N with the above properties is definable by a
![]() $\Sigma _1$
-formula with parameter U, we can conclude that the set
$\Sigma _1$
-formula with parameter U, we can conclude that the set
![]() $\{\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}\}$
is definable by a
$\{\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
.
The techniques used in the above proofs also allow us to prove the second part of Theorem 4.6:
Proof of Theorem 4.6
Let
![]() $\kappa $
be a limit of measurable cardinals. Then, Lemma 4.10 shows that every unbounded subset of
$\kappa $
be a limit of measurable cardinals. Then, Lemma 4.10 shows that every unbounded subset of
![]() $\kappa $
that consists of cardinals is
$\kappa $
that consists of cardinals is
![]() $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary. Now, let S be a
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary. Now, let S be a
![]() $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of
![]() $\kappa $
, and let
$\kappa $
, and let
![]() ${r}:{\kappa }\longrightarrow {\kappa }$
be a regressive function that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
be a regressive function that is definable by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
, an ordinal
$\varphi (v_0,\ldots ,v_3)$
, an ordinal
![]() $\gamma $
, and an element z of
$\gamma $
, and an element z of
![]() $\mathrm {H}_{\kappa }$
. As in the proof of Lemma 4.11, we can now find a measurable cardinal
$\mathrm {H}_{\kappa }$
. As in the proof of Lemma 4.11, we can now find a measurable cardinal
![]() $\kappa _0<\kappa $
with
$\kappa _0<\kappa $
with
![]() $z\in \mathrm {H}_{\kappa _0}$
and a normal ultrafilter U on
$z\in \mathrm {H}_{\kappa _0}$
and a normal ultrafilter U on
![]() $\kappa _0$
with the property that
$\kappa _0$
with the property that
![]() $j_{0,\alpha }(\gamma )=\gamma $
holds for all
$j_{0,\alpha }(\gamma )=\gamma $
holds for all
![]() $\alpha <\kappa $
, where
$\alpha <\kappa $
, where
denotes the linear iteration of
![]() $\langle V,\in ,U\rangle $
. Let
$\langle V,\in ,U\rangle $
. Let
![]() $r(\kappa _0)=\xi <\kappa _0$
. Then,
$r(\kappa _0)=\xi <\kappa _0$
. Then,
![]() $\varphi (\kappa _0,\xi ,\gamma ,z)$
holds in V, and for all
$\varphi (\kappa _0,\xi ,\gamma ,z)$
holds in V, and for all
![]() $\alpha <\kappa $
, elementarity implies that
$\alpha <\kappa $
, elementarity implies that
![]() $\varphi (j_{0,\alpha }(\kappa _0),\xi ,\gamma ,z)$
holds in
$\varphi (j_{0,\alpha }(\kappa _0),\xi ,\gamma ,z)$
holds in
![]() $M_\alpha $
. Given
$M_\alpha $
. Given
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $\Sigma _1$
-upwards absoluteness now implies that
$\Sigma _1$
-upwards absoluteness now implies that
![]() $\varphi (j_{0,\alpha }(\kappa _0),\xi ,\gamma ,z)$
holds in V, and hence,
$\varphi (j_{0,\alpha }(\kappa _0),\xi ,\gamma ,z)$
holds in V, and hence,
![]() $r(j_{0,\alpha }(\kappa _0))=\xi $
. This shows that the restriction of r to the closed unbounded subset
$r(j_{0,\alpha }(\kappa _0))=\xi $
. This shows that the restriction of r to the closed unbounded subset
![]() $C=\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}$
of
$C=\{{j_{0,\alpha }(\kappa _0)}~\vert ~{\alpha <\kappa }\}$
of
![]() $\kappa $
is constant with value
$\kappa $
is constant with value
![]() $\xi $
. Moreover, the proof of Lemma 4.11 shows that the set
$\xi $
. Moreover, the proof of Lemma 4.11 shows that the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\kappa $
and U. Since Corollary 2.11 and Lemma 4.10 show that the set
$\kappa $
and U. Since Corollary 2.11 and Lemma 4.10 show that the set
![]() $C\cap S$
is
$C\cap S$
is
![]() $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
![]() $\kappa $
, these arguments show that r is constant on a
$\kappa $
, these arguments show that r is constant on a
![]() $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of S.
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary subset of S.
4.3 Partition properties
Remember that, given uncountable cardinals
![]() $\mu <\kappa $
, the cardinal
$\mu <\kappa $
, the cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\mu $
-Rowbottom if the square brackets partition relation
$\mu $
-Rowbottom if the square brackets partition relation
![]() $\kappa \longrightarrow [\kappa ]^{{<}\omega }_{\lambda ,{<}\mu }$
holds true for all
$\kappa \longrightarrow [\kappa ]^{{<}\omega }_{\lambda ,{<}\mu }$
holds true for all
![]() $\lambda <\kappa $
(i.e., for every
$\lambda <\kappa $
(i.e., for every
![]() $\lambda <\kappa $
and every function
$\lambda <\kappa $
and every function
![]() ${c}:{[\kappa ]^{{<}\omega }}\longrightarrow {\lambda }$
, there exists
${c}:{[\kappa ]^{{<}\omega }}\longrightarrow {\lambda }$
, there exists
![]() $H\in [\kappa ]^\kappa $
with the property that
$H\in [\kappa ]^\kappa $
with the property that
![]() $\vert {c[[H]^{{<}\omega }]}\vert <\mu $
). Moreover,
$\vert {c[[H]^{{<}\omega }]}\vert <\mu $
). Moreover,
![]() $\omega _1$
-Rowbottom cardinals are called Rowbottom cardinals. The following lemma connects this partition property to the
$\omega _1$
-Rowbottom cardinals are called Rowbottom cardinals. The following lemma connects this partition property to the
![]() $\boldsymbol {\Sigma }_1$
-undefinability property:
$\boldsymbol {\Sigma }_1$
-undefinability property:
Lemma 4.12 Let
![]() $\kappa $
be a
$\kappa $
be a
![]() $\mu $
-Rowbottom cardinal. If either
$\mu $
-Rowbottom cardinal. If either
![]() $\kappa =\omega _\omega $
or
$\kappa =\omega _\omega $
or
![]() $\rho ^{{<}\mu }<\kappa $
holds for all
$\rho ^{{<}\mu }<\kappa $
holds for all
![]() $\rho <\kappa $
, then
$\rho <\kappa $
, then
![]() $\kappa $
has the
$\kappa $
has the
![]() $\Sigma _1(\mu )$
-undefinability property.
$\Sigma _1(\mu )$
-undefinability property.
Proof Assume, toward a contradiction, that there is a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
, an element z of
$\varphi (v_0,v_1,v_2)$
, an element z of
![]() $\mathrm {H}_{\mu }$
, and an ordinal
$\mathrm {H}_{\mu }$
, and an ordinal
![]() $\alpha $
in
$\alpha $
in
![]() $[\mu ,\kappa )$
that is the unique set x such that
$[\mu ,\kappa )$
that is the unique set x such that
![]() $\varphi (x,\kappa ,z)$
holds.
$\varphi (x,\kappa ,z)$
holds.
Claim There exists an elementary submodel X of
![]() $\mathrm {H}_{\kappa ^+}$
satisfying
$\mathrm {H}_{\kappa ^+}$
satisfying
![]() $\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
,
$\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
,
![]() $\vert {X\cap \alpha }\vert <\vert {\alpha }\vert $
and
$\vert {X\cap \alpha }\vert <\vert {\alpha }\vert $
and
![]() $\vert {X\cap \kappa }\vert =\kappa $
.
$\vert {X\cap \kappa }\vert =\kappa $
.
Proof of the Claim
Define
![]() $\mathcal {L}$
to be the countable first-order language that extends
$\mathcal {L}$
to be the countable first-order language that extends
![]() $\mathcal {L}_\in $
by a unary predicate symbol
$\mathcal {L}_\in $
by a unary predicate symbol
![]() $\dot {P}$
, a unary function symbol
$\dot {P}$
, a unary function symbol
![]() $\dot {s}$
, a constant symbol
$\dot {s}$
, a constant symbol
![]() $\dot {\kappa }$
, a constant symbol
$\dot {\kappa }$
, a constant symbol
![]() $\dot {\alpha }$
, and a constant symbol
$\dot {\alpha }$
, and a constant symbol
![]() $\dot {c}_y$
for every
$\dot {c}_y$
for every
![]() $y\in \mathrm {{tc}}({\{z\}})$
. Pick an elementary submodel M of
$y\in \mathrm {{tc}}({\{z\}})$
. Pick an elementary submodel M of
![]() $\mathrm {H}_{\kappa ^+}$
of cardinality
$\mathrm {H}_{\kappa ^+}$
of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $\mathrm {{tc}}({\{z\}})\cup (\kappa +1)\subseteq M$
and a surjection
$\mathrm {{tc}}({\{z\}})\cup (\kappa +1)\subseteq M$
and a surjection
![]() ${s}:{\kappa }\longrightarrow {M}$
. Now, let A denote an
${s}:{\kappa }\longrightarrow {M}$
. Now, let A denote an
![]() $\mathcal {L}$
-expansion of
$\mathcal {L}$
-expansion of
![]() $\langle M,\in \rangle $
with
$\langle M,\in \rangle $
with
![]() $\dot {P}^A=\alpha $
,
$\dot {P}^A=\alpha $
,
![]() $\dot {s}^A\restriction \kappa =s$
,
$\dot {s}^A\restriction \kappa =s$
,
![]() $\dot {\kappa }^A=\kappa $
,
$\dot {\kappa }^A=\kappa $
,
![]() $\dot {\alpha }^A=\alpha $
, and
$\dot {\alpha }^A=\alpha $
, and
![]() $\dot {c}_y^A=y$
for all
$\dot {c}_y^A=y$
for all
![]() $y\in \mathrm {{tc}}({\{z\}})$
. In addition, we define
$y\in \mathrm {{tc}}({\{z\}})$
. In addition, we define
![]() $\rho =\vert {\alpha }\vert \geq \mu $
.
$\rho =\vert {\alpha }\vert \geq \mu $
.
First, assume that
![]() $\rho ^{{<}\mu }<\kappa $
holds. Then, [Reference Kanamori10, Theorem 8.5] yields an elementary substructure X of A of cardinality
$\rho ^{{<}\mu }<\kappa $
holds. Then, [Reference Kanamori10, Theorem 8.5] yields an elementary substructure X of A of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $\vert {X\cap \alpha }\vert <\mu \leq \rho $
. This setup then ensures that
$\vert {X\cap \alpha }\vert <\mu \leq \rho $
. This setup then ensures that
![]() $\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
, and since
$\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
, and since
![]() ${\mathrm {{ran}}(s\restriction X)}=X$
, we also know that
${\mathrm {{ran}}(s\restriction X)}=X$
, we also know that
![]() $\vert {X\cap \kappa }\vert =\kappa $
.
$\vert {X\cap \kappa }\vert =\kappa $
.
In the other case, assume that
![]() $\kappa =\omega _\omega $
. Then,
$\kappa =\omega _\omega $
. Then,
![]() $\rho $
is regular and
$\rho $
is regular and
![]() $\kappa $
is also
$\kappa $
is also
![]() $\rho $
-Rowbottom. Another application of [Reference Kanamori10, Theorem 8.5] now produces an elementary substructure X of A of cardinality
$\rho $
-Rowbottom. Another application of [Reference Kanamori10, Theorem 8.5] now produces an elementary substructure X of A of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $\vert {X\cap \alpha }\vert <\rho $
. As above, we can conclude that
$\vert {X\cap \alpha }\vert <\rho $
. As above, we can conclude that
![]() $\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
and
$\mathrm {{tc}}({\{z\}})\cup \{\kappa ,\alpha \}\subseteq X$
and
![]() $\vert {X\cap \kappa }\vert =\kappa $
.
$\vert {X\cap \kappa }\vert =\kappa $
.
Let
![]() ${\pi }:{X}\longrightarrow {N}$
denote the corresponding transitive collapse. Then, our setup ensures that
${\pi }:{X}\longrightarrow {N}$
denote the corresponding transitive collapse. Then, our setup ensures that
![]() $\pi (\kappa )=\kappa $
,
$\pi (\kappa )=\kappa $
,
![]() $\pi (z)=z$
, and
$\pi (z)=z$
, and
![]() $\pi (\alpha )<\alpha $
. Moreover, since
$\pi (\alpha )<\alpha $
. Moreover, since
![]() $\Sigma _1$
-absoluteness causes
$\Sigma _1$
-absoluteness causes
![]() $\varphi (\alpha ,\kappa ,z)$
to hold in
$\varphi (\alpha ,\kappa ,z)$
to hold in
![]() $\mathrm {H}_{\kappa ^+}$
and X, we know that
$\mathrm {H}_{\kappa ^+}$
and X, we know that
![]() $\varphi (\pi (\alpha ),\kappa ,z)$
holds in N. But then,
$\varphi (\pi (\alpha ),\kappa ,z)$
holds in N. But then,
![]() $\Sigma _1$
-upwards absoluteness implies that this statement holds in V, contradicting our assumptions.
$\Sigma _1$
-upwards absoluteness implies that this statement holds in V, contradicting our assumptions.
Recall that a cardinal
![]() $\kappa $
is Jónsson if for every function
$\kappa $
is Jónsson if for every function
![]() ${f}:{[\kappa ]^{{<}\omega }}\longrightarrow {\kappa }$
, there is a proper subset H of
${f}:{[\kappa ]^{{<}\omega }}\longrightarrow {\kappa }$
, there is a proper subset H of
![]() $\kappa $
of cardinality
$\kappa $
of cardinality
![]() $\kappa $
with
$\kappa $
with
![]() $f[[H]^{{<}\omega }]\subseteq H$
. Motivated by the notoriously open question whether the first limit cardinal
$f[[H]^{{<}\omega }]\subseteq H$
. Motivated by the notoriously open question whether the first limit cardinal
![]() $\omega _\omega $
can be Jónsson, we show that this assumption causes analogs of central results from the previous two sections to hold at
$\omega _\omega $
can be Jónsson, we show that this assumption causes analogs of central results from the previous two sections to hold at
![]() $\omega _\omega $
.
$\omega _\omega $
.
Theorem 4.13 If
![]() $\omega _\omega $
is a Jónsson cardinal, then the following statements hold:
$\omega _\omega $
is a Jónsson cardinal, then the following statements hold:
-
(1) Every infinite subset of
 $\{{\omega _n}~\vert ~{n<\omega }\}$
is
$\{{\omega _n}~\vert ~{n<\omega }\}$
is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\omega _\omega $
.
$\omega _\omega $
. -
(2) If
 ${r}:{\omega _\omega }\longrightarrow {\omega _\omega }$
is a regressive function that is definable by a
${r}:{\omega _\omega }\longrightarrow {\omega _\omega }$
is a regressive function that is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 $\mathrm {H}_{\aleph _\omega }\cup \{\omega _\omega \}$
, then r is constant on an infinite subset of
$\mathrm {H}_{\aleph _\omega }\cup \{\omega _\omega \}$
, then r is constant on an infinite subset of
 $\{{\omega _n}~\vert ~{n<\omega }\}$
.
$\{{\omega _n}~\vert ~{n<\omega }\}$
.
Proof Since
![]() $\omega _\omega $
is the least Jónsson cardinal, we know that
$\omega _\omega $
is the least Jónsson cardinal, we know that
![]() $\omega _\omega $
is
$\omega _\omega $
is
![]() $\omega _n$
-Rowbottom for some
$\omega _n$
-Rowbottom for some
![]() $0<n<\omega $
(see [Reference Kanamori10, Proposition 8.15]). Then, Lemma 4.12 implies that
$0<n<\omega $
(see [Reference Kanamori10, Proposition 8.15]). Then, Lemma 4.12 implies that
![]() $\omega _\omega $
has the
$\omega _\omega $
has the
![]() $\Sigma _1(\omega _k)$
-undefinability property for all
$\Sigma _1(\omega _k)$
-undefinability property for all
![]() $n\leq k<\omega $
. An application of Corollary 2.13 then shows that every infinite subset of
$n\leq k<\omega $
. An application of Corollary 2.13 then shows that every infinite subset of
![]() $\{{\omega _m}~\vert ~{m<\omega }\}$
is
$\{{\omega _m}~\vert ~{m<\omega }\}$
is
![]() $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
![]() $\omega _\omega $
.
$\omega _\omega $
.
Now, assume that
![]() ${r}:{\omega _\omega }\longrightarrow {\omega _\omega }$
is a regressive function that is definable by a
${r}:{\omega _\omega }\longrightarrow {\omega _\omega }$
is a regressive function that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\aleph _\omega }\cup \{\omega _\omega \}$
. Then, we can find
$\mathrm {H}_{\aleph _\omega }\cup \{\omega _\omega \}$
. Then, we can find
![]() $0<n<\omega $
and
$0<n<\omega $
and
![]() $z\in \mathrm {H}_{\aleph _n}$
such that
$z\in \mathrm {H}_{\aleph _n}$
such that
![]() $\omega _\omega $
is
$\omega _\omega $
is
![]() $\omega _n$
-Rowbottom and r is definable by a
$\omega _n$
-Rowbottom and r is definable by a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
and the parameters
$\varphi (v_0,\ldots ,v_3)$
and the parameters
![]() $\omega _\omega $
and z. By repeating the proof of Lemma 4.12, we can find an elementary submodel X of
$\omega _\omega $
and z. By repeating the proof of Lemma 4.12, we can find an elementary submodel X of
![]() $\mathrm {H}_{\aleph _{\omega +1}}$
with
$\mathrm {H}_{\aleph _{\omega +1}}$
with
![]() $\mathrm {{tc}}({\{z\}})\cup \{\kappa \}\subseteq X$
,
$\mathrm {{tc}}({\{z\}})\cup \{\kappa \}\subseteq X$
,
![]() $\vert {X\cap \omega _\omega }\vert =\aleph _\omega $
, and
$\vert {X\cap \omega _\omega }\vert =\aleph _\omega $
, and
![]() $\vert {X\cap \omega _n}\vert =\aleph _{n-1}$
. Let
$\vert {X\cap \omega _n}\vert =\aleph _{n-1}$
. Let
![]() ${\pi }:{X}\longrightarrow {N}$
denote the corresponding transitive collapse. Then,
${\pi }:{X}\longrightarrow {N}$
denote the corresponding transitive collapse. Then,
![]() $\omega _\omega \in N$
,
$\omega _\omega \in N$
,
![]() $\pi (\omega _\omega )=\omega _\omega $
and
$\pi (\omega _\omega )=\omega _\omega $
and
![]() $\omega _n\in {\mathrm {{ran}}(\pi )}$
. Set
$\omega _n\in {\mathrm {{ran}}(\pi )}$
. Set
![]() $\lambda =\pi ^{{-}1}(\omega _n)<\omega _n$
. Then,
$\lambda =\pi ^{{-}1}(\omega _n)<\omega _n$
. Then,
![]() $\pi \restriction \lambda =\mathrm {{id}}_\lambda $
, and an easy induction shows that
$\pi \restriction \lambda =\mathrm {{id}}_\lambda $
, and an easy induction shows that
![]() $\pi (\omega _k)<\omega _k$
holds for all
$\pi (\omega _k)<\omega _k$
holds for all
![]() $n\leq k<\omega $
. In particular, we know that
$n\leq k<\omega $
. In particular, we know that
![]() $\pi ^{{-}1}(\alpha )>\alpha $
holds for all
$\pi ^{{-}1}(\alpha )>\alpha $
holds for all
![]() $\omega _n\leq \alpha <\omega _\omega $
. By elementarity, the formula
$\omega _n\leq \alpha <\omega _\omega $
. By elementarity, the formula
![]() $\varphi (v_0,\ldots ,v_3)$
and the parameters
$\varphi (v_0,\ldots ,v_3)$
and the parameters
![]() $\omega _\omega $
and z define a regressive function in N. In particular,
$\omega _\omega $
and z define a regressive function in N. In particular,
![]() $\Sigma _1$
-upwards absoluteness implies that
$\Sigma _1$
-upwards absoluteness implies that
![]() $\varphi (\alpha ,r(\alpha ),\omega _\omega ,z)$
holds in N for all
$\varphi (\alpha ,r(\alpha ),\omega _\omega ,z)$
holds in N for all
![]() $\alpha <\omega _\omega $
. We now define a strictly increasing sequence
$\alpha <\omega _\omega $
. We now define a strictly increasing sequence
![]() $\langle {\mu _i}~\vert ~{i<\omega }\rangle $
of ordinals in the interval
$\langle {\mu _i}~\vert ~{i<\omega }\rangle $
of ordinals in the interval
![]() $[\omega _n,\omega _\omega )$
by setting
$[\omega _n,\omega _\omega )$
by setting
![]() $\mu _0=\omega _n$
and
$\mu _0=\omega _n$
and
![]() $\mu _{i+1}=\pi ^{{-}1}(\mu _i)$
for all
$\mu _{i+1}=\pi ^{{-}1}(\mu _i)$
for all
![]() $i<\omega $
. We can then inductively show that each
$i<\omega $
. We can then inductively show that each
![]() $\mu _i$
is a cardinal with
$\mu _i$
is a cardinal with
![]() $r(\mu _i)=r(\lambda )$
, and hence, r is constant on an infinite subset of
$r(\mu _i)=r(\lambda )$
, and hence, r is constant on an infinite subset of
![]() $\{{\omega _m}~\vert ~{m<\omega }\}$
.
$\{{\omega _m}~\vert ~{m<\omega }\}$
.
We end this section by presenting an example of an application of the concepts isolated in this paper to reduce the class of models of set theory in which
![]() $\omega _\omega $
possesses strong partition properties. In particular, we will show that
$\omega _\omega $
possesses strong partition properties. In particular, we will show that
![]() $\omega _\omega $
is not
$\omega _\omega $
is not
![]() $\omega _2$
-Rowbottom in the standard models of strong forcing axioms, where the given axiom was forced over a model of the
$\omega _2$
-Rowbottom in the standard models of strong forcing axioms, where the given axiom was forced over a model of the
![]() $\mathrm {{GCH}}$
by turning some large cardinal into
$\mathrm {{GCH}}$
by turning some large cardinal into
![]() $\omega _2$
. This implication will be a direct consequence of the following observation:
$\omega _2$
. This implication will be a direct consequence of the following observation:
Lemma 4.14 Assume that there is a natural number
![]() $n_*>1$
such that there are no special
$n_*>1$
such that there are no special
![]() $\omega _{n_*}$
-Aronszajn trees, and for all
$\omega _{n_*}$
-Aronszajn trees, and for all
![]() $n_*<n<\omega $
, there are special
$n_*<n<\omega $
, there are special
![]() $\omega _n$
-Aronszajn trees. Then, the set
$\omega _n$
-Aronszajn trees. Then, the set
![]() $\{\omega _{n_*}\}$
is definable by a
$\{\omega _{n_*}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _\omega $
, and the cardinal
$\omega _\omega $
, and the cardinal
![]() $\omega _\omega $
is not
$\omega _\omega $
is not
![]() $\omega _{n_*}$
-Rowbottom.
$\omega _{n_*}$
-Rowbottom.
Proof Consider the collection of all transitive models M of
![]() $\mathrm {{ZFC}}^-$
with the following properties:
$\mathrm {{ZFC}}^-$
with the following properties:
-
•
 $\omega _\omega +1\subseteq M$
.
$\omega _\omega +1\subseteq M$
. -
•
 $\omega _\omega =\omega _\omega ^M$
.
$\omega _\omega =\omega _\omega ^M$
. -
• In M, for every
 $n_*<n<\omega $
, there is a special
$n_*<n<\omega $
, there is a special
 $\omega ^M_n$
-Aronszajn tree.
$\omega ^M_n$
-Aronszajn tree.
The collection of such models M is not empty as it includes
![]() $\mathrm {H}_{\aleph _{\omega +1}}$
. It is clear that for each model M in this collection, we have
$\mathrm {H}_{\aleph _{\omega +1}}$
. It is clear that for each model M in this collection, we have
![]() $\omega _{n_*}^M = \omega _{n_*}$
. Hence, we can conclude that the set
$\omega _{n_*}^M = \omega _{n_*}$
. Hence, we can conclude that the set
![]() $\{\omega _{n_*}\}$
is definable by the
$\{\omega _{n_*}\}$
is definable by the
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _\omega $
that says there is a model M with the above properties and x is equal to
$\omega _\omega $
that says there is a model M with the above properties and x is equal to
![]() $\omega _{n_*}^M$
. In particular, this shows that the cardinal
$\omega _{n_*}^M$
. In particular, this shows that the cardinal
![]() $\omega _\omega $
does not have the
$\omega _\omega $
does not have the
![]() $\Sigma _1(\omega _{n_*})$
-undefinability property, and hence, Lemma 4.12 shows that
$\Sigma _1(\omega _{n_*})$
-undefinability property, and hence, Lemma 4.12 shows that
![]() $\omega _\omega $
is not
$\omega _\omega $
is not
![]() $\omega _{n_*}$
-Rowbottom.
$\omega _{n_*}$
-Rowbottom.
If we start in a model of the
![]() $\mathrm {{GCH}}$
containing a supercompact cardinal and use the canonical forcing to force the validity of some strong forcing axiom, like
$\mathrm {{GCH}}$
containing a supercompact cardinal and use the canonical forcing to force the validity of some strong forcing axiom, like
![]() $\mathrm {{PFA}}$
or
$\mathrm {{PFA}}$
or
![]() $\mathrm {{M}}\mathrm {{M}}^{++}$
, then a result of Baumgartner shows that the tree property holds at
$\mathrm {{M}}\mathrm {{M}}^{++}$
, then a result of Baumgartner shows that the tree property holds at
![]() $\omega _2$
, and since the
$\omega _2$
, and since the
![]() $\mathrm {{GCH}}$
holds above
$\mathrm {{GCH}}$
holds above
![]() $\aleph _0$
, a result of Specker ensures that there are special
$\aleph _0$
, a result of Specker ensures that there are special
![]() $\omega _n$
-Aronszajn trees for all
$\omega _n$
-Aronszajn trees for all
![]() $2<n<\omega $
. Therefore, the above lemma shows that
$2<n<\omega $
. Therefore, the above lemma shows that
![]() $\omega _\omega $
is not
$\omega _\omega $
is not
![]() $\omega _2$
-Rowbottom in these models. This observation should be compared with the consistency results of König in [Reference König12].
$\omega _2$
-Rowbottom in these models. This observation should be compared with the consistency results of König in [Reference König12].
5 Equiconsistency results
We build on the results of the previous sections to obtain more equiconsistency results that witness various ways by which different types of
![]() $\Sigma _1$
-definable closed unbounded sets of cardinals
$\Sigma _1$
-definable closed unbounded sets of cardinals
![]() $\kappa $
fail to approximate the closed unbounded filter on
$\kappa $
fail to approximate the closed unbounded filter on
![]() $\kappa $
.
$\kappa $
.
5.1 Limits of uncountably many measurable cardinals
We start by showing that, in the case of singular cardinals of uncountable cofinality, Theorem 4.6 provides the right consistency strength for both of the listed conclusions. In contrast, we will later show that the consistency strength for singular cardinals of countable cofinality is merely a single measurable cardinal.
Theorem 5.1 Let
![]() $\kappa $
be a singular cardinal of uncountable cofinality. If there is no inner model with
$\kappa $
be a singular cardinal of uncountable cofinality. If there is no inner model with
![]() ${\mathrm {{cof}}(\kappa )}$
-many measurable cardinals, then the following statements hold:
${\mathrm {{cof}}(\kappa )}$
-many measurable cardinals, then the following statements hold:
-
(1) Every subset of
 $\kappa $
that is
$\kappa $
that is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
is stationary in
$\kappa $
is stationary in
 $\kappa $
. In particular, there is an unbounded subset of
$\kappa $
. In particular, there is an unbounded subset of
 $\kappa $
that consists of cardinals and is not
$\kappa $
that consists of cardinals and is not
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
.
$\kappa $
. -
(2) There exists a regressive function
 ${r}:{\kappa }\longrightarrow {\kappa }$
that is definable by a
${r}:{\kappa }\longrightarrow {\kappa }$
that is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 $\mathrm {H}_{\kappa }\cup \{\kappa \}$
and is not constant on any unbounded subset of
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
and is not constant on any unbounded subset of
 $\kappa $
.
$\kappa $
.
Proof By [Reference Koepke11, Theorem 2.14], our assumptions imply that
![]() $0^{long}$
(as defined in [Reference Koepke11, Definition 2.13]) does not exist. Let
$0^{long}$
(as defined in [Reference Koepke11, Definition 2.13]) does not exist. Let
![]() $U_{can}$
denote the canonical sequence of measures, and let
$U_{can}$
denote the canonical sequence of measures, and let
![]() $\mathrm {{K}}[U_{can}]$
denote the canonical core model (as defined in [Reference Koepke11, Definition 3.15]). Then, our assumption ensures that
$\mathrm {{K}}[U_{can}]$
denote the canonical core model (as defined in [Reference Koepke11, Definition 3.15]). Then, our assumption ensures that
![]() ${\mathrm {{dom}}(U_{can})}$
has order-type less than
${\mathrm {{dom}}(U_{can})}$
has order-type less than
![]() ${\mathrm {{cof}}(\kappa )}$
. Moreover, since
${\mathrm {{cof}}(\kappa )}$
. Moreover, since
![]() ${\mathrm {{cof}}(\kappa )}$
is uncountable, we can apply [Reference Koepke11, Theorem 3.23] to show that
${\mathrm {{cof}}(\kappa )}$
is uncountable, we can apply [Reference Koepke11, Theorem 3.23] to show that
![]() $\kappa $
is not measurable in
$\kappa $
is not measurable in
![]() $\mathrm {{K}}[U_{can}]$
. But this allows us to use [Reference Koepke11, Theorem 3.20] to conclude that
$\mathrm {{K}}[U_{can}]$
. But this allows us to use [Reference Koepke11, Theorem 3.20] to conclude that
![]() $\kappa $
is singular in
$\kappa $
is singular in
![]() $\mathrm {{K}}[U_{can}]$
. Set
$\mathrm {{K}}[U_{can}]$
. Set
![]() $U=U_{can}\restriction \kappa $
and
$U=U_{can}\restriction \kappa $
and
![]() $\mathrm {{K}}=\mathrm {{K}}[U]$
(see [Reference Koepke11, Definition 3.1]). Then,
$\mathrm {{K}}=\mathrm {{K}}[U]$
(see [Reference Koepke11, Definition 3.1]). Then,
![]() $U\in \mathrm {H}_{\kappa }$
and [Reference Koepke11, Theorem 3.9] shows that
$U\in \mathrm {H}_{\kappa }$
and [Reference Koepke11, Theorem 3.9] shows that
![]() ${\mathcal {P}}({\kappa })^{\mathrm {{K}}[U_{can}]}\subseteq \mathrm {{K}}$
. In particular, we know that
${\mathcal {P}}({\kappa })^{\mathrm {{K}}[U_{can}]}\subseteq \mathrm {{K}}$
. In particular, we know that
![]() $\kappa $
is singular in
$\kappa $
is singular in
![]() $\mathrm {{K}}$
, and we can define
$\mathrm {{K}}$
, and we can define
![]() $c:\mathrm {cof}(\kappa )^{\mathrm {K}}\longrightarrow \kappa $
to be the
$c:\mathrm {cof}(\kappa )^{\mathrm {K}}\longrightarrow \kappa $
to be the
![]() $<_{\mathrm {K}[U]}$
-least cofinal function in
$<_{\mathrm {K}[U]}$
-least cofinal function in
![]() $\mathrm {K}$
(see [Reference Koepke11, Theorem 3.4]). Then, [Reference Lücke and Schlicht16, Lemma 2.3] shows that c is definable by a
$\mathrm {K}$
(see [Reference Koepke11, Theorem 3.4]). Then, [Reference Lücke and Schlicht16, Lemma 2.3] shows that c is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. But this shows that there is a closed unbounded subset C of
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. But this shows that there is a closed unbounded subset C of
![]() $\kappa $
of order-type
$\kappa $
of order-type
![]() $\mathrm {cof}(\kappa )^{\mathrm {K}}$
such that
$\mathrm {cof}(\kappa )^{\mathrm {K}}$
such that
![]() $\min (C)>{\mathrm {cof}(\kappa )}^{\mathrm {K}}$
, and the set
$\min (C)>{\mathrm {cof}(\kappa )}^{\mathrm {K}}$
, and the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. As in the proof of Corollary 3.4, we now know that every subset of
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. As in the proof of Corollary 3.4, we now know that every subset of
![]() $\kappa $
that is
$\kappa $
that is
![]() $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
![]() $\kappa $
is stationary in
$\kappa $
is stationary in
![]() $\kappa $
. Finally, the function
$\kappa $
. Finally, the function
is a regressive function that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
and is not constant on any unbounded subset of
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
and is not constant on any unbounded subset of
![]() $\kappa $
.
$\kappa $
.
By combining this result with Theorem 4.6, we obtain the following equiconsistency:
Corollary 5.2 The following statements are equiconsistent over
![]() $\mathrm {{ZFC}}$
:
$\mathrm {{ZFC}}$
:
-
(1) There exist uncountably many measurable cardinals.
-
(2) There exists a singular cardinal
 $\kappa $
of uncountable cofinality with the property that some nonstationary subset of
$\kappa $
of uncountable cofinality with the property that some nonstationary subset of
 $\kappa $
is
$\kappa $
is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
.
$\kappa $
. -
(3) There exists a singular cardinal
 $\kappa $
of uncountable cofinality with the property that some nonstationary subset of
$\kappa $
of uncountable cofinality with the property that some nonstationary subset of
 $\kappa $
is
$\kappa $
is
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
 $\kappa $
.
$\kappa $
.
5.2 Countable cofinalities
The aim of this section is to prove the following equiconsistency result:
Theorem 5.3 The following statements are equiconsistent over
![]() $\mathrm {{ZFC}}$
:
$\mathrm {{ZFC}}$
:
-
(1) There is a measurable cardinal.
-
(2) Every unbounded subset of
 $\{{\omega _n}~\vert ~{n<\omega }\}$
is
$\{{\omega _n}~\vert ~{n<\omega }\}$
is
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
 $\omega _\omega $
.
$\omega _\omega $
. -
(3) There is a singular cardinal
 $\kappa $
of countable cofinality and a subset of
$\kappa $
of countable cofinality and a subset of
 $\kappa $
that consists of cardinals and is
$\kappa $
that consists of cardinals and is
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary in
 $\kappa $
.
$\kappa $
. -
(4) There is a singular cardinal
 $\kappa $
of countable cofinality and a subset of
$\kappa $
of countable cofinality and a subset of
 $\kappa $
that consists of cardinals and is
$\kappa $
that consists of cardinals and is
 $\boldsymbol {\Sigma }_1$
-stationary in
$\boldsymbol {\Sigma }_1$
-stationary in
 $\kappa $
.
$\kappa $
.
Remark 5.4 The restriction to
![]() $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-definability in (2) of the theorem is optimal since the sequence
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-definability in (2) of the theorem is optimal since the sequence
![]() $\langle {\omega _n}~\vert ~{n < \omega }\rangle $
is
$\langle {\omega _n}~\vert ~{n < \omega }\rangle $
is
![]() $\Sigma _2(\mathrm{Ord})$
-definable.
$\Sigma _2(\mathrm{Ord})$
-definable.
In the following arguments, we will make use of the Easton-support collapse version from [Reference Shioya18] of a universal collapse forcing (see [Reference Foreman6] for a comprehensive background).
Definition 5.1 Suppose that
![]() $\kappa $
is a Mahlo cardinal, and let
$\kappa $
is a Mahlo cardinal, and let
For each
![]() $\gamma \in I_\kappa $
, we define
$\gamma \in I_\kappa $
, we define
![]() $\mathbb {Q}(\gamma ,{<}\kappa )$
to be the product
$\mathbb {Q}(\gamma ,{<}\kappa )$
to be the product
with the Easton-support.
Remark 5.5 The partial order
![]() $\mathbb {Q}(\gamma ,{<}\kappa )$
is clearly definable from the ordinals
$\mathbb {Q}(\gamma ,{<}\kappa )$
is clearly definable from the ordinals
![]() $\gamma $
and
$\gamma $
and
![]() $\kappa $
, and forcing with
$\kappa $
, and forcing with
![]() $\mathbb {Q}(\gamma ,{<}\kappa )$
collapses all cardinals in the interval
$\mathbb {Q}(\gamma ,{<}\kappa )$
collapses all cardinals in the interval
![]() $(\gamma ,\kappa )$
. Since this partial order is
$(\gamma ,\kappa )$
. Since this partial order is
![]() ${<}\gamma $
-closed and satisfies the
${<}\gamma $
-closed and satisfies the
![]() $\kappa $
-chain condition, the cardinal
$\kappa $
-chain condition, the cardinal
![]() $\kappa $
becomes
$\kappa $
becomes
![]() $\gamma ^+$
in
$\gamma ^+$
in
![]() $\mathbb {Q}(\gamma ,{<}\kappa )$
-generic extensions. In the following, we will rely on the following two useful features of this partial order:
$\mathbb {Q}(\gamma ,{<}\kappa )$
-generic extensions. In the following, we will rely on the following two useful features of this partial order:
-
(1) If
 $\delta <\kappa $
is a Mahlo cardinal and
$\delta <\kappa $
is a Mahlo cardinal and
 $\gamma \in I_\delta $
, then
$\gamma \in I_\delta $
, then
 $\mathbb {Q}(\gamma ,{<}\delta ) \times \mathbb {Q}(\delta ,{<}\kappa )$
is a regular subforcing of
$\mathbb {Q}(\gamma ,{<}\delta ) \times \mathbb {Q}(\delta ,{<}\kappa )$
is a regular subforcing of
 $\mathbb {Q}(\gamma ,{<}\kappa )$
.
$\mathbb {Q}(\gamma ,{<}\kappa )$
. -
(2)
 $\mathbb {Q}(\gamma ,{<}\kappa )$
is weakly homogeneous.
$\mathbb {Q}(\gamma ,{<}\kappa )$
is weakly homogeneous.
The proofs are left to the reader (see also [Reference Shioya18]).
Before proving Theorem 5.3, we review some basic facts about Prikry forcing and products of collapse forcings. Suppose that
![]() $\kappa $
is a measurable cardinal and U is a normal measure on
$\kappa $
is a measurable cardinal and U is a normal measure on
![]() $\kappa $
. We let
$\kappa $
. We let
![]() $\mathbb {P}_U$
denote the Prikry forcing given by U. Conditions
$\mathbb {P}_U$
denote the Prikry forcing given by U. Conditions
![]() $\mathbb {P}_U$
are then of the form
$\mathbb {P}_U$
are then of the form
![]() $p = \langle s_p, A_p\rangle $
, where
$p = \langle s_p, A_p\rangle $
, where
![]() $s_p \in [\kappa ]^{{<}\omega }$
is a finite sequence of Mahlo cardinals and
$s_p \in [\kappa ]^{{<}\omega }$
is a finite sequence of Mahlo cardinals and
![]() $A_p \in U$
consists of Mahlo cardinals and satisfies
$A_p \in U$
consists of Mahlo cardinals and satisfies
![]() $\min (A_p)> \max (s_p)$
. We then have
$\min (A_p)> \max (s_p)$
. We then have
![]() $p\leq _{\mathbb {P}_U}q$
if
$p\leq _{\mathbb {P}_U}q$
if
![]() $s_p$
end-extends
$s_p$
end-extends
![]() $s_q$
,
$s_q$
,
![]() $A_p \subseteq A_q$
, and
$A_p \subseteq A_q$
, and
![]() $s_p\setminus s_q \subseteq A_q$
. If, moreover,
$s_p\setminus s_q \subseteq A_q$
. If, moreover,
![]() $s_p = s_q$
holds, then we say p is a direct extension of q, denoted by
$s_p = s_q$
holds, then we say p is a direct extension of q, denoted by
![]() $p \leq _{\mathbb {P}_U}^* q$
. Given a condition p in
$p \leq _{\mathbb {P}_U}^* q$
. Given a condition p in
![]() $\mathbb {P}_U$
and
$\mathbb {P}_U$
and
![]() $t\in [A_p]^{{<}\omega }$
, we let
$t\in [A_p]^{{<}\omega }$
, we let
![]() $p{}^\frown t$
denote the condition
$p{}^\frown t$
denote the condition
![]() $\langle s_p\cup t,A_p\setminus (\max (t)+1)\rangle $
. Finally, if G is
$\langle s_p\cup t,A_p\setminus (\max (t)+1)\rangle $
. Finally, if G is
![]() $\mathbb {P}_U$
-generic filter over V, then its associated Prikry sequence
$\mathbb {P}_U$
-generic filter over V, then its associated Prikry sequence
![]() $\vec {\kappa }^{\hspace {0.7pt}G} = \langle {\kappa ^G_n}~\vert ~{n<\omega }\rangle $
is defined by
$\vec {\kappa }^{\hspace {0.7pt}G} = \langle {\kappa ^G_n}~\vert ~{n<\omega }\rangle $
is defined by
![]() $\vec {\kappa }^{\hspace {0.7pt}G} = \bigcup \{{s\in [\kappa ]^{<\omega }}~\vert ~{\exists A \in U ~ \langle s,A\rangle \in G}\}$
. Below, we record some of the basic properties of
$\vec {\kappa }^{\hspace {0.7pt}G} = \bigcup \{{s\in [\kappa ]^{<\omega }}~\vert ~{\exists A \in U ~ \langle s,A\rangle \in G}\}$
. Below, we record some of the basic properties of
![]() $\mathbb {P}_U$
that will be used in the following arguments (see [Reference Gitik8] for details).
$\mathbb {P}_U$
that will be used in the following arguments (see [Reference Gitik8] for details).
Fact 5.6
-
(1) The direct extension order
 $\leq ^*_{\mathbb {P}_U}$
is
$\leq ^*_{\mathbb {P}_U}$
is
 ${<}\kappa $
-closed.
${<}\kappa $
-closed. -
(2) Forcing with
 $\mathbb {P}_U$
does not introduce new bounded subsets of
$\mathbb {P}_U$
does not introduce new bounded subsets of
 $\kappa $
.
$\kappa $
. -
(3) The partial order
 $\mathbb {P}_U$
satisfies the
$\mathbb {P}_U$
satisfies the
 $\kappa ^+$
-chain condition.
$\kappa ^+$
-chain condition. -
(4) (Prikry Property) For every condition q in
 $\mathbb {P}_U$
and every statement
$\mathbb {P}_U$
and every statement
 $\sigma $
in the forcing language of
$\sigma $
in the forcing language of
 $\mathbb {P}_U$
, there is
$\mathbb {P}_U$
, there is
 $p \leq ^*_{\mathbb {P}_U} q$
which decides
$p \leq ^*_{\mathbb {P}_U} q$
which decides
 $\sigma $
.
$\sigma $
. -
(5) (Strong Prikry Property) For every condition q in
 $\mathbb {P}_U$
and every dense open set D of
$\mathbb {P}_U$
and every dense open set D of
 $\mathbb {P}_U$
, there is
$\mathbb {P}_U$
, there is
 $p \leq _{\mathbb {P}_U}^* q$
and
$p \leq _{\mathbb {P}_U}^* q$
and
 $n < \omega $
such that D contains all conditions of the form
$n < \omega $
such that D contains all conditions of the form
 $p{}^\frown t$
with
$p{}^\frown t$
with
 $t\in [A_p]^n$
.
$t\in [A_p]^n$
. -
(6) (Name-Capturing Property) For every condition q in
 $\mathbb {P}_U$
and every
$\mathbb {P}_U$
and every
 $\mathbb {P}_U$
-name
$\mathbb {P}_U$
-name
 $\dot {f}$
for a function with domain
$\dot {f}$
for a function with domain
 $\omega $
with the property that
$\omega $
with the property that
 $\dot {f}^G(n)\in \mathrm {H}_{\kappa _n^G}$
holds whenever
$\dot {f}^G(n)\in \mathrm {H}_{\kappa _n^G}$
holds whenever
 $n<\omega $
and G is
$n<\omega $
and G is
 $\mathbb {P}_U$
-generic over V with
$\mathbb {P}_U$
-generic over V with
 $q\in G$
, there is a condition
$q\in G$
, there is a condition
 $p \leq _{\mathbb {P}_U}^* q$
and a function
$p \leq _{\mathbb {P}_U}^* q$
and a function
 ${F}:{[A_p]^{{<}\omega }}\longrightarrow \mathrm {{H}_{\kappa }}$
so that holds for every
${F}:{[A_p]^{{<}\omega }}\longrightarrow \mathrm {{H}_{\kappa }}$
so that holds for every $$ \begin{align*}p{}^\frown t \Vdash_{\mathbb{P}_U}{\text{"}\hspace{0.3ex}{\dot{f}(\vert \check{s}_p \cup \check{t}\vert) = \check{F}(\check{t})}\hspace{0.3ex}\text{"}}\end{align*} $$
$$ \begin{align*}p{}^\frown t \Vdash_{\mathbb{P}_U}{\text{"}\hspace{0.3ex}{\dot{f}(\vert \check{s}_p \cup \check{t}\vert) = \check{F}(\check{t})}\hspace{0.3ex}\text{"}}\end{align*} $$
 $t \in [A^*]^{{<}\omega }$
.
$t \in [A^*]^{{<}\omega }$
.
-
(7) A
 $\mathbb {P}_U$
-generic filter G is generated by its induced Prikry sequence
$\mathbb {P}_U$
-generic filter G is generated by its induced Prikry sequence
 $\vec {\kappa }^{\hspace {0.7pt}G}$
in the sense that
$\vec {\kappa }^{\hspace {0.7pt}G}$
in the sense that
 $G = \{{ \langle \vec {\kappa }^{\hspace {0.7pt}G}\upharpoonright n, A\rangle }~\vert ~{n<\omega , ~ \vec {\kappa }^{\hspace {0.7pt}G}\setminus n \subseteq A\in U}\}$
.
$G = \{{ \langle \vec {\kappa }^{\hspace {0.7pt}G}\upharpoonright n, A\rangle }~\vert ~{n<\omega , ~ \vec {\kappa }^{\hspace {0.7pt}G}\setminus n \subseteq A\in U}\}$
. -
(8) (Mathias Criterion) A sequence
 $\vec {\kappa } = \langle {\kappa _n}~\vert ~{n<\omega }\rangle $
generates a
$\vec {\kappa } = \langle {\kappa _n}~\vert ~{n<\omega }\rangle $
generates a
 $\mathbb {P}_U$
-generic filter if and only if
$\mathbb {P}_U$
-generic filter if and only if
 $\vec {\kappa }\setminus A$
is finite for every
$\vec {\kappa }\setminus A$
is finite for every
 $A \in U$
.
$A \in U$
.
To push the construction down to
![]() $\omega _\omega $
, we force with a product of collapse posets after adding a Prikry forcing. Let
$\omega _\omega $
, we force with a product of collapse posets after adding a Prikry forcing. Let
![]() $\vec {\rho } = \langle {\rho _n}~\vert ~{n< \ell _{\vec {\rho }}}\rangle $
be a strictly increasing sequence of Mahlo cardinals of length
$\vec {\rho } = \langle {\rho _n}~\vert ~{n< \ell _{\vec {\rho }}}\rangle $
be a strictly increasing sequence of Mahlo cardinals of length
![]() $0<\ell _{\vec {\rho }} \leq \omega $
and define
$0<\ell _{\vec {\rho }} \leq \omega $
and define
![]() $\mathbb {C}_{\vec {\rho }}$
to be the product
$\mathbb {C}_{\vec {\rho }}$
to be the product
with full support. Therefore, conditions in
![]() $\mathbb {C}_{\vec {\rho }}$
are sequences
$\mathbb {C}_{\vec {\rho }}$
are sequences
![]() $q = \langle {q_n}~\vert ~{n < \ell _{\vec {\rho }}}\rangle $
with
$q = \langle {q_n}~\vert ~{n < \ell _{\vec {\rho }}}\rangle $
with
![]() $q_0 \in \mathbb {Q}(\omega ,{<}\rho _0)$
and
$q_0 \in \mathbb {Q}(\omega ,{<}\rho _0)$
and
![]() $q_n \in \mathbb {Q}(\rho _{n-1},{<}\rho _{n})$
for all
$q_n \in \mathbb {Q}(\rho _{n-1},{<}\rho _{n})$
for all
![]() $0<n<\ell _{\vec {\rho }}$
.
$0<n<\ell _{\vec {\rho }}$
.
Remark 5.7
-
(1) Standard arguments about product forcings show that if G is
 ${\mathbb {C}_{\vec {\rho }}\hspace {1.2pt}}$
-generic over V, then
${\mathbb {C}_{\vec {\rho }}\hspace {1.2pt}}$
-generic over V, then
 $\rho _n=\omega _{n+1}^{V[G]}$
holds for every
$\rho _n=\omega _{n+1}^{V[G]}$
holds for every
 $n<\ell _{\vec {\rho }}$
.
$n<\ell _{\vec {\rho }}$
. -
(2) By the absorption argument for the Easton-support collapse product (Remark 5.5), if s is a finite strictly increasing sequences of Mahlo cardinals and t is a subsequence of s with
 $\max (s) = \max (t)$
, then
$\max (s) = \max (t)$
, then
 $\mathbb {C}_s$
is a regular subforcing of
$\mathbb {C}_s$
is a regular subforcing of
 $\mathbb {C}_t$
. This directly implies that if
$\mathbb {C}_t$
. This directly implies that if
 $\vec {\rho }$
is a strictly increasing sequence of Mahlo cardinals of length
$\vec {\rho }$
is a strictly increasing sequence of Mahlo cardinals of length
 $\omega $
and s is a finite subset of
$\omega $
and s is a finite subset of
 $\vec {\rho }$
, then
$\vec {\rho }$
, then
 $\mathbb {C}_{\vec {\rho }}$
is a regular subforcing of
$\mathbb {C}_{\vec {\rho }}$
is a regular subforcing of
 $\mathbb {C}_{\vec {\rho }\hspace {1.1pt}\setminus s}$
. Moreover, the associated forcing projection from
$\mathbb {C}_{\vec {\rho }\hspace {1.1pt}\setminus s}$
. Moreover, the associated forcing projection from
 $\mathbb {C}_{\vec {\rho }\hspace {1.1pt}\setminus s}$
to
$\mathbb {C}_{\vec {\rho }\hspace {1.1pt}\setminus s}$
to
 $\mathbb {C}_{\vec {\rho }}$
is the identity on the components below
$\mathbb {C}_{\vec {\rho }}$
is the identity on the components below
 $\min (s)$
and above
$\min (s)$
and above
 $\min \left (\vec {\rho } \setminus (\max (s)+1)\right )$
.
$\min \left (\vec {\rho } \setminus (\max (s)+1)\right )$
. -
(3) The forcing
 $\mathbb {C}_{\vec {\rho }}$
is weakly homogeneous. Therefore, if some condition in
$\mathbb {C}_{\vec {\rho }}$
is weakly homogeneous. Therefore, if some condition in
 $\mathbb {C}_{\vec {\rho }}$
forces a statement with ground model parameters to hold, then every condition forces this statement to hold. Similarly, for every sequence
$\mathbb {C}_{\vec {\rho }}$
forces a statement with ground model parameters to hold, then every condition forces this statement to hold. Similarly, for every sequence
 $\vec {\rho }$
and an initial segment s, the quotient forcing
$\vec {\rho }$
and an initial segment s, the quotient forcing
 $\mathbb {C}_{\vec {\rho }}/\mathbb {C}_{s}$
is also weakly homogeneous.
$\mathbb {C}_{\vec {\rho }}/\mathbb {C}_{s}$
is also weakly homogeneous.
In the following, let
![]() $\dot {\mathbb {C}}$
denote the canonical
$\dot {\mathbb {C}}$
denote the canonical
![]() $\mathbb {P}_U$
-name for a partial order with the property that
$\mathbb {P}_U$
-name for a partial order with the property that
![]() $\dot {\mathbb {C}}^G=\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}}$
holds whenever G is
$\dot {\mathbb {C}}^G=\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}}$
holds whenever G is
![]() $\mathbb {P}_U$
-generic over V. The argument of the following Lemma will give the forcing direction of Theorem 5.3.
$\mathbb {P}_U$
-generic over V. The argument of the following Lemma will give the forcing direction of Theorem 5.3.
Lemma 5.8 If
![]() $G * H$
is
$G * H$
is
![]() $(\mathbb {P}_U*\dot {\mathbb {C}})$
-generic over V and
$(\mathbb {P}_U*\dot {\mathbb {C}})$
-generic over V and
![]() $\gamma \geq \kappa $
is an ordinal, then in
$\gamma \geq \kappa $
is an ordinal, then in
![]() $V[G,H]$
, the cardinal
$V[G,H]$
, the cardinal
![]() $\omega _\omega $
has the
$\omega _\omega $
has the
![]() $\Sigma _1(\omega _n,\gamma )$
-undefinability property for all sufficiently large natural numbers n.
$\Sigma _1(\omega _n,\gamma )$
-undefinability property for all sufficiently large natural numbers n.
Proof Fix a condition
![]() $p_*$
in
$p_*$
in
![]() $\mathbb {P}_U$
. For each natural number
$\mathbb {P}_U$
. For each natural number
![]() $n\geq \vert s_{p_*}\vert $
, let
$n\geq \vert s_{p_*}\vert $
, let
![]() $\sigma _n$
be the statement in the forcing language of
$\sigma _n$
be the statement in the forcing language of
![]() $\mathbb {P}_U$
that says that there is a condition in
$\mathbb {P}_U$
that says that there is a condition in
![]() $\dot {\mathbb {C}}$
which forces that
$\dot {\mathbb {C}}$
which forces that
![]() $\kappa $
does not have the
$\kappa $
does not have the
![]() $\Sigma _1(\dot {\kappa }_n,\gamma )$
-undefinability property, where
$\Sigma _1(\dot {\kappa }_n,\gamma )$
-undefinability property, where
![]() $\dot {\kappa }_n$
denotes the canonical
$\dot {\kappa }_n$
denotes the canonical
![]() $\mathbb {P}_U$
-name for
$\mathbb {P}_U$
-name for
![]() $\kappa _n^G$
. By the Prikry property, for each
$\kappa _n^G$
. By the Prikry property, for each
![]() $\vert s_{p_*}\vert \leq n<\omega $
, there is a condition
$\vert s_{p_*}\vert \leq n<\omega $
, there is a condition
![]() $p_n\leq ^*_{\mathbb {P}_U}p_*$
that decides
$p_n\leq ^*_{\mathbb {P}_U}p_*$
that decides
![]() $\sigma _n$
. We complete the proof by showing that for all
$\sigma _n$
. We complete the proof by showing that for all
![]() $\vert s_{p_*}\vert \leq n<\omega $
, the condition
$\vert s_{p_*}\vert \leq n<\omega $
, the condition
![]() $p_n$
forces
$p_n$
forces
![]() $\neg \sigma _n$
to hold. Suppose otherwise that
$\neg \sigma _n$
to hold. Suppose otherwise that
![]() $p_n\Vdash _{\mathbb {P}_U}\sigma _n$
for some
$p_n\Vdash _{\mathbb {P}_U}\sigma _n$
for some
![]() $\vert s_{p_*}\vert \leq n<\omega $
. Pick a condition
$\vert s_{p_*}\vert \leq n<\omega $
. Pick a condition
![]() $p\leq _{\mathbb {P}_U}p_n$
with
$p\leq _{\mathbb {P}_U}p_n$
with
![]() $\vert {s_p}\vert =n$
. Since
$\vert {s_p}\vert =n$
. Since
![]() $p \Vdash _{\mathbb {P}_U} \sigma _n$
, there is a
$p \Vdash _{\mathbb {P}_U} \sigma _n$
, there is a
![]() $\mathbb {P}_U$
-name
$\mathbb {P}_U$
-name
![]() $\dot {q}$
for a condition in
$\dot {q}$
for a condition in
![]() $\dot {\mathbb {C}}$
so that
$\dot {\mathbb {C}}$
so that
Since
![]() $\dot {\kappa }_n$
is a
$\dot {\kappa }_n$
is a
![]() $\mathbb {P}_U$
-name and
$\mathbb {P}_U$
-name and
![]() $\dot {\mathbb {C}}$
is forced to be weakly homogeneous (see Remark 5.7), we can assume that
$\dot {\mathbb {C}}$
is forced to be weakly homogeneous (see Remark 5.7), we can assume that
![]() $\dot {q}$
is the name for the trivial condition
$\dot {q}$
is the name for the trivial condition ![]() in
in
![]() $\dot {\mathbb {C}}$
. This allows us to find
$\dot {\mathbb {C}}$
. This allows us to find
![]() $(\mathbb {P}_U * \dot {\mathbb {C}})$
-names
$(\mathbb {P}_U * \dot {\mathbb {C}})$
-names
![]() $\dot {x}$
,
$\dot {x}$
,
![]() $\dot {\alpha }$
, and
$\dot {\alpha }$
, and
![]() $\dot {\tau }$
so that
$\dot {\tau }$
so that ![]() forces the following statements to hold:
forces the following statements to hold:
-
•
 $\dot {x}$
is an element of
$\dot {x}$
is an element of
 $\mathrm {H}_{\dot {\kappa }_n}$
.
$\mathrm {H}_{\dot {\kappa }_n}$
. -
•
 $\dot {\alpha }$
is an ordinal in the interval
$\dot {\alpha }$
is an ordinal in the interval
 $[\dot {\kappa }_n,\check {\kappa })$
.
$[\dot {\kappa }_n,\check {\kappa })$
. -
•
 $\dot {\tau }$
is the Gödel number of a
$\dot {\tau }$
is the Gödel number of a
 $\Sigma _1$
-formula
$\Sigma _1$
-formula
 $\varphi (v_0,\ldots ,v_3)$
that defines the set
$\varphi (v_0,\ldots ,v_3)$
that defines the set
 $\{\dot {\alpha }\}$
using the parameters
$\{\dot {\alpha }\}$
using the parameters
 $\check {\kappa }$
,
$\check {\kappa }$
,
 $\check {\gamma },$
and
$\check {\gamma },$
and
 $\dot {x}$
.
$\dot {x}$
.
Making another use of the fact that
![]() $\dot {\mathbb {C}}$
is forced to be a weakly homogeneous partial order, we may assume
$\dot {\mathbb {C}}$
is forced to be a weakly homogeneous partial order, we may assume
![]() $\dot {\alpha }$
and
$\dot {\alpha }$
and
![]() $\dot {\tau }$
are
$\dot {\tau }$
are
![]() $\mathbb {P}_U$
-names. Moreover, using the Prikry property of
$\mathbb {P}_U$
-names. Moreover, using the Prikry property of
![]() $\mathbb {P}_U$
, we may also assume that p decides that
$\mathbb {P}_U$
, we may also assume that p decides that
![]() $\dot {\tau }$
codes a given
$\dot {\tau }$
codes a given
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_3)$
. Since the quotient forcing
$\varphi (v_0,\ldots ,v_3)$
. Since the quotient forcing
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}}/\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
is weakly homogeneous whenever G is
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}}/\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
is weakly homogeneous whenever G is
![]() $\mathbb {P}_U$
-generic over V, we may assume that
$\mathbb {P}_U$
-generic over V, we may assume that
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $(\mathbb {P}_U*\dot {\mathbb {C}}_n)$
-name, where
$(\mathbb {P}_U*\dot {\mathbb {C}}_n)$
-name, where
![]() $\dot {\mathbb {C}}_n$
is the canonical
$\dot {\mathbb {C}}_n$
is the canonical
![]() $\mathbb {P}_U$
-name for
$\mathbb {P}_U$
-name for
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
. In addition, since forcing with
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
. In addition, since forcing with
![]() $\mathbb {P}_U$
does not add new bounded sets to
$\mathbb {P}_U$
does not add new bounded sets to
![]() $\kappa $
and
$\kappa $
and
![]() $\dot {\mathbb {C}}_n$
is forced to satisfy the
$\dot {\mathbb {C}}_n$
is forced to satisfy the
![]() $\dot {\kappa }_n$
-chain condition, there is a
$\dot {\kappa }_n$
-chain condition, there is a
![]() $\mathbb {P}_U$
-name
$\mathbb {P}_U$
-name
![]() $\dot {y}$
with the property that whenever G is
$\dot {y}$
with the property that whenever G is
![]() $\mathbb {P}_U$
-generic over V with
$\mathbb {P}_U$
-generic over V with
![]() $p\in G$
, then
$p\in G$
, then
![]() $\dot {y}^G$
is a
$\dot {y}^G$
is a
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
-name in
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
-name in
![]() $\mathrm {H}_{\kappa _n^G}^V$
that
$\mathrm {H}_{\kappa _n^G}^V$
that
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
forces to be equal to
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G}\restriction (n+1)}$
forces to be equal to
![]() $\dot {x}$
. The fact that
$\dot {x}$
. The fact that
![]() $p{}^\frown \langle \rho \rangle \Vdash _{\mathbb {P}_U}{\text {"}\hspace {0.3ex}{\dot {\kappa }_n=\check {\rho }}\hspace {0.3ex}\text {"}}$
holds for every
$p{}^\frown \langle \rho \rangle \Vdash _{\mathbb {P}_U}{\text {"}\hspace {0.3ex}{\dot {\kappa }_n=\check {\rho }}\hspace {0.3ex}\text {"}}$
holds for every
![]() $\rho \in A_p$
allows us to use the name-capturing property of
$\rho \in A_p$
allows us to use the name-capturing property of
![]() $\mathbb {P}_U$
(see Fact 5.6) to find a function
$\mathbb {P}_U$
(see Fact 5.6) to find a function
![]() ${Y}:{A_p}\longrightarrow \mathrm {{H}_{\kappa }}$
with the property that for every
${Y}:{A_p}\longrightarrow \mathrm {{H}_{\kappa }}$
with the property that for every
![]() $\rho \in A_p$
, the set
$\rho \in A_p$
, the set
![]() $Y(\rho )$
is a
$Y(\rho )$
is a
![]() $\mathbb {C}_{s_p\cup \{\rho \}}$
-name in
$\mathbb {C}_{s_p\cup \{\rho \}}$
-name in
![]() $\mathrm {H}_{\rho }$
with
$\mathrm {H}_{\rho }$
with
![]() $p{}^\frown \langle \rho \rangle \Vdash _{\mathbb {P}_U}{\text {"}\hspace {0.3ex}{\dot {y}=\check {Y}(\check {\rho }).}\hspace {0.3ex}\text {"}}$
Using the normality of U, we can find
$p{}^\frown \langle \rho \rangle \Vdash _{\mathbb {P}_U}{\text {"}\hspace {0.3ex}{\dot {y}=\check {Y}(\check {\rho }).}\hspace {0.3ex}\text {"}}$
Using the normality of U, we can find
![]() $A\subseteq A_p$
in U and
$A\subseteq A_p$
in U and
![]() $\dot {y}_0$
in
$\dot {y}_0$
in
![]() $\mathrm {H}_{\kappa }$
with the property that
$\mathrm {H}_{\kappa }$
with the property that
![]() $Y(\rho )=\dot {y}_0$
holds for all
$Y(\rho )=\dot {y}_0$
holds for all
![]() $\rho \in A$
. Let
$\rho \in A$
. Let
![]() $\rho _0 = \min (A)$
. Then, we can find an ordinal
$\rho _0 = \min (A)$
. Then, we can find an ordinal
![]() $\alpha $
in the interval
$\alpha $
in the interval
![]() $[\rho _0,\kappa )$
and a condition
$[\rho _0,\kappa )$
and a condition
![]() $r_0\leq _{\mathbb {P}_U}p{}^\frown \langle \rho _0\rangle $
with
$r_0\leq _{\mathbb {P}_U}p{}^\frown \langle \rho _0\rangle $
with
![]() $\alpha <\max (s_{r_0})$
and
$\alpha <\max (s_{r_0})$
and
![]() $r_0\Vdash _{\mathbb {P}_U}{\text {"}\hspace {0.3ex}{\dot {\alpha }=\check {\alpha }.}\hspace {0.3ex}\text {"}}$
Set
$r_0\Vdash _{\mathbb {P}_U}{\text {"}\hspace {0.3ex}{\dot {\alpha }=\check {\alpha }.}\hspace {0.3ex}\text {"}}$
Set
![]() $\rho _1=\min (A\cap A_{r_0})$
and
$\rho _1=\min (A\cap A_{r_0})$
and
![]() $r_1=\langle s_p\cup \{\rho _1\},A_{r_0}\setminus (\rho _1+1)\rangle $
. Then,
$r_1=\langle s_p\cup \{\rho _1\},A_{r_0}\setminus (\rho _1+1)\rangle $
. Then,
![]() $r_1$
is a condition in
$r_1$
is a condition in
![]() $\mathbb {P}_U$
that strengthens
$\mathbb {P}_U$
that strengthens
![]() $p{}^\frown \langle \rho _1\rangle $
. Let
$p{}^\frown \langle \rho _1\rangle $
. Let
![]() $G_1*H_1$
be
$G_1*H_1$
be
![]() $(\mathbb {P}_U*\dot {\mathbb {C}})$
-generic over V with
$(\mathbb {P}_U*\dot {\mathbb {C}})$
-generic over V with
![]() $r_1\in G_1$
. We then have
$r_1\in G_1$
. We then have
![]() $\kappa _n^{G_1}=\rho _1>\max (s_{r_0})>\alpha $
. By the Mathias criterion for
$\kappa _n^{G_1}=\rho _1>\max (s_{r_0})>\alpha $
. By the Mathias criterion for
![]() $\mathbb {P}_U$
(see Fact 5.6), the sequence
$\mathbb {P}_U$
(see Fact 5.6), the sequence
![]() $s_{r_0}{}^\frown (\vec {\kappa }^{\hspace {0.7pt}G_1}\restriction [n,\omega ))$
generates a
$s_{r_0}{}^\frown (\vec {\kappa }^{\hspace {0.7pt}G_1}\restriction [n,\omega ))$
generates a
![]() $\mathbb {P}_U$
-generic filter
$\mathbb {P}_U$
-generic filter
![]() $G_0$
over V that is an element of
$G_0$
over V that is an element of
![]() $V[G_1]$
. It is then clear that
$V[G_1]$
. It is then clear that
![]() $r_0$
is an element of
$r_0$
is an element of
![]() $G_0$
and
$G_0$
and
![]() $V[G_0]=V[G_1]$
. Moreover, since
$V[G_0]=V[G_1]$
. Moreover, since
![]() $\vec {\kappa }^{\hspace {0.7pt}G_1}\restriction n=s_p=s_{r_0}\restriction n$
, it follows that
$\vec {\kappa }^{\hspace {0.7pt}G_1}\restriction n=s_p=s_{r_0}\restriction n$
, it follows that
![]() $\vec {\kappa }^{\hspace {0.7pt}G_1}$
is a subsequence of
$\vec {\kappa }^{\hspace {0.7pt}G_1}$
is a subsequence of
![]() $\vec {\kappa }^{\hspace {0.7pt}G_0}$
with finite difference, and hence, the absorption property of Easton collapse posets (see Remark 5.5) ensures that the partial order
$\vec {\kappa }^{\hspace {0.7pt}G_0}$
with finite difference, and hence, the absorption property of Easton collapse posets (see Remark 5.5) ensures that the partial order
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G_0}}$
is a regular subforcing of the partial order
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G_0}}$
is a regular subforcing of the partial order
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G_1}}$
. Let
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G_1}}$
. Let
![]() $H_0\in V[G_0,H_1]$
denote the filter on
$H_0\in V[G_0,H_1]$
denote the filter on
![]() $\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G_0}}$
induced by
$\mathbb {C}_{\vec {\kappa }^{\hspace {0.7pt}G_0}}$
induced by
![]() $H_1$
. Since
$H_1$
. Since
![]() $H_0$
and
$H_0$
and
![]() $H_1$
induce the same filter on
$H_1$
induce the same filter on
![]() $\mathbb {C}_{s_p\cup \{\rho _0\}}$
, we know that
$\mathbb {C}_{s_p\cup \{\rho _0\}}$
, we know that
![]() $\dot {y}_0^{H_0}=\dot {y}_0^{H_1}$
. This implies that
$\dot {y}_0^{H_0}=\dot {y}_0^{H_1}$
. This implies that
![]() $\varphi (\alpha ,\kappa ,\gamma ,\dot {y}_0^{H_1})$
holds in
$\varphi (\alpha ,\kappa ,\gamma ,\dot {y}_0^{H_1})$
holds in
![]() $V[G_0,H_0]$
, and by
$V[G_0,H_0]$
, and by
![]() $\Sigma _1$
-upwards absoluteness, this statement also holds in
$\Sigma _1$
-upwards absoluteness, this statement also holds in
![]() $V[G_0,H_1]$
. But this yields a contradiction because the fact that
$V[G_0,H_1]$
. But this yields a contradiction because the fact that
![]() $r_1$
is an element of
$r_1$
is an element of
![]() $G_1$
implies that
$G_1$
implies that
![]() $\dot {\alpha }^{G_1}\geq \kappa _n^{G_1}=\rho _1>\alpha $
and
$\dot {\alpha }^{G_1}\geq \kappa _n^{G_1}=\rho _1>\alpha $
and
![]() $\dot {\alpha }^{G_1}$
is the unique element a of
$\dot {\alpha }^{G_1}$
is the unique element a of
![]() $V[G_0,H_1]$
with the property that
$V[G_0,H_1]$
with the property that
![]() $\varphi (a,\kappa ,\gamma ,\dot {y}_0^{H_1})$
holds.
$\varphi (a,\kappa ,\gamma ,\dot {y}_0^{H_1})$
holds.
A combination of the above lemma with Corollary 2.13 now directly yields the following result:
Corollary 5.9 If
![]() $G * H$
is
$G * H$
is
![]() $(\mathbb {P}_U*\dot {\mathbb {C}})$
-generic over V, then in
$(\mathbb {P}_U*\dot {\mathbb {C}})$
-generic over V, then in
![]() $V[G,H]$
, every unbounded subset of
$V[G,H]$
, every unbounded subset of
![]() $\{{\omega _n}~\vert ~{n<\omega }\}$
is
$\{{\omega _n}~\vert ~{n<\omega }\}$
is
![]() $\boldsymbol {\Sigma }_1(\mathrm {{\mathrm{Ord}}})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm {{\mathrm{Ord}}})$
-stationary in
![]() $\omega _\omega $
.
$\omega _\omega $
.
We are now ready to prove the main result of this section:
Proof of Theorem 5.3
First, let
![]() $\kappa $
be a singular cardinal of countable cofinality, and let E be a subset of
$\kappa $
be a singular cardinal of countable cofinality, and let E be a subset of
![]() $\kappa $
that consists of cardinals and is
$\kappa $
that consists of cardinals and is
![]() $\boldsymbol {\Sigma }_1(\mathrm {{\mathrm{Ord}}})$
-stationary in
$\boldsymbol {\Sigma }_1(\mathrm {{\mathrm{Ord}}})$
-stationary in
![]() $\kappa $
. Assume, toward contradiction, that there is no inner model with a measurable cardinal. Then,
$\kappa $
. Assume, toward contradiction, that there is no inner model with a measurable cardinal. Then,
![]() $\kappa $
is singular in the Dodd-Jensen core model
$\kappa $
is singular in the Dodd-Jensen core model
![]() $\mathrm {{K}}^{DJ}$
. By Lemma 3.3, there is a cofinal function
$\mathrm {{K}}^{DJ}$
. By Lemma 3.3, there is a cofinal function
![]() ${c}:{{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}\longrightarrow {\kappa }$
which is definable by a
${c}:{{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}\longrightarrow {\kappa }$
which is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
. In addition, pick a cofinal function
$\kappa $
. In addition, pick a cofinal function
![]() ${g}:{\omega }\longrightarrow {{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}$
. Then the composition
${g}:{\omega }\longrightarrow {{\mathrm {{cof}}(\kappa )}^{\mathrm {{K}}^{DJ}}}$
. Then the composition
![]() ${f = c \circ g}:{\omega }\longrightarrow {\kappa }$
is cofinal in
${f = c \circ g}:{\omega }\longrightarrow {\kappa }$
is cofinal in
![]() $\kappa $
and
$\kappa $
and
![]() $\Sigma _1$
-definable from the parameters
$\Sigma _1$
-definable from the parameters
![]() $\kappa $
and
$\kappa $
and
![]() $g \in \mathrm {H}_{\kappa }$
. Then, the
$g \in \mathrm {H}_{\kappa }$
. Then, the
![]() $C = \{{ f(n)+1}~\vert ~{n < \omega }\}$
is closed unbounded in
$C = \{{ f(n)+1}~\vert ~{n < \omega }\}$
is closed unbounded in
![]() $\kappa $
, and it is definable by a
$\kappa $
, and it is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Since it consists of successor ordinals, it is disjoint from E, contradicting our assumptions.
$\mathrm {H}_{\kappa }\cup \{\kappa \}$
. Since it consists of successor ordinals, it is disjoint from E, contradicting our assumptions.
The above computations show that (4) implies (1) in the statement of the theorem. This completes the proof of the theorem because the implications from (2) to (3) and from (3) to (4) are trivial, and the implication from (1) to (2) is given by Corollary 5.9.
By combining Theorem 5.3 with the second part of Corollary 3.6, we derive the following equiconsistency result that shows that the statement of Proposition 2.8 is optimal in
![]() $\mathrm {{ZFC}}$
.
$\mathrm {{ZFC}}$
.
Corollary 5.10 The following statements are equiconsistent over
![]() $\mathrm {{ZFC}}$
:
$\mathrm {{ZFC}}$
:
-
(1) There is a measurable cardinal.
-
(2) There is a singular cardinal
 $\kappa $
of countable cofinality with the property that for every subset A of
$\kappa $
of countable cofinality with the property that for every subset A of
 $\mathrm {H}_{\kappa }$
of cardinality
$\mathrm {H}_{\kappa }$
of cardinality
 $\mathfrak {r}$
, there exists a subset E of
$\mathfrak {r}$
, there exists a subset E of
 $\kappa $
such that both E and
$\kappa $
such that both E and
 $\kappa \setminus E$
are
$\kappa \setminus E$
are
 $\Sigma _1(A)$
-stationary.
$\Sigma _1(A)$
-stationary. -
(3) There is a singular cardinal
 $\kappa $
of countable cofinality with the property that there exists a subset E of
$\kappa $
of countable cofinality with the property that there exists a subset E of
 $\kappa $
such that both E and
$\kappa $
such that both E and
 $\kappa \setminus E$
are
$\kappa \setminus E$
are
 $\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary.
$\boldsymbol {\Sigma }_1(\mathrm{Ord})$
-stationary.
5.3 Successors of regular cardinals
We continue by studying
![]() $\Sigma _1(A)$
-stationary subsets of successor cardinals. In this section, we prove the following equiconsistency result for successors of regular cardinals:
$\Sigma _1(A)$
-stationary subsets of successor cardinals. In this section, we prove the following equiconsistency result for successors of regular cardinals:
Theorem 5.11 The following statements are equiconsistent over
![]() $\mathrm {{ZFC}}$
:
$\mathrm {{ZFC}}$
:
-
(1) There is a Mahlo cardinal.
-
(2) There is a regular cardinal
 $\mu $
with the property that the set
$\mu $
with the property that the set
 $\{\mu \}$
is
$\{\mu \}$
is
 $\Sigma _1(\mathrm {H}_{\mu })$
-stationary in
$\Sigma _1(\mathrm {H}_{\mu })$
-stationary in
 $\mu ^+$
.
$\mu ^+$
. -
(3) There is a regular cardinal
 $\mu $
with the property that the set
$\mu $
with the property that the set
 $\{\mu \}$
is
$\{\mu \}$
is
 $\Sigma _1$
-stationary in
$\Sigma _1$
-stationary in
 $\mu ^+$
.
$\mu ^+$
.
Lemma 5.12 If
![]() $\kappa $
is a Mahlo cardinal, then there exists an inaccessible cardinal
$\kappa $
is a Mahlo cardinal, then there exists an inaccessible cardinal
![]() $\delta <\kappa $
with the property that
$\delta <\kappa $
with the property that
![]() $\mathbb {Q}(\delta ,{<}\kappa )$
forces
$\mathbb {Q}(\delta ,{<}\kappa )$
forces
![]() $\kappa $
to have the
$\kappa $
to have the
![]() $\Sigma _1(\delta )$
-undefinability property.
$\Sigma _1(\delta )$
-undefinability property.
Proof Assume, toward a contradiction, that no such
![]() $\delta $
exists. Then, for every inaccessible
$\delta $
exists. Then, for every inaccessible
![]() $\gamma \in I_\kappa $
, the fact that
$\gamma \in I_\kappa $
, the fact that
![]() $\mathbb {Q}(\gamma ,{<}\kappa )$
is weakly homogeneous (see Remarks 5.5 and 5.7) allows us to find
$\mathbb {Q}(\gamma ,{<}\kappa )$
is weakly homogeneous (see Remarks 5.5 and 5.7) allows us to find
![]() $x_\gamma $
,
$x_\gamma $
,
![]() $\alpha _\gamma $
, and
$\alpha _\gamma $
, and
![]() $\tau _\gamma $
such that the following statements hold:
$\tau _\gamma $
such that the following statements hold:
-
•
 $x_\gamma $
is an element of
$x_\gamma $
is an element of
 $\mathrm {H}_{\gamma }$
.
$\mathrm {H}_{\gamma }$
. -
•
 $\alpha _\gamma $
is an ordinal in the interval
$\alpha _\gamma $
is an ordinal in the interval
 $[\gamma ,\kappa )$
.
$[\gamma ,\kappa )$
. -
•
 $\tau _\gamma $
is a Gödel number of a
$\tau _\gamma $
is a Gödel number of a
 $\Sigma _1$
-formula
$\Sigma _1$
-formula
 $\varphi (v_0,v_1,v_2)$
with the property that the trivial condition of
$\varphi (v_0,v_1,v_2)$
with the property that the trivial condition of
 $\mathbb {Q}(\gamma ,{<}\kappa )$
forces that
$\mathbb {Q}(\gamma ,{<}\kappa )$
forces that
 $\alpha _\gamma $
is the unique set a such that
$\alpha _\gamma $
is the unique set a such that
 $\varphi (a,\kappa ,x_\gamma )$
holds.
$\varphi (a,\kappa ,x_\gamma )$
holds.
Since
![]() $\kappa $
is a Mahlo cardinal, we can find a stationary subset S of
$\kappa $
is a Mahlo cardinal, we can find a stationary subset S of
![]() $\kappa $
consisting of inaccessible cardinals, an element x of
$\kappa $
consisting of inaccessible cardinals, an element x of
![]() $\mathrm {H}_{\kappa }$
, and a
$\mathrm {H}_{\kappa }$
, and a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
such that for all
$\varphi (v_0,v_1,v_2)$
such that for all
![]() $\gamma \in S$
, we have
$\gamma \in S$
, we have
![]() $x_\gamma =x$
and
$x_\gamma =x$
and
![]() $\tau _\gamma $
is a Gödel number of
$\tau _\gamma $
is a Gödel number of
![]() $\varphi (v_0,v_1,v_2)$
. Let
$\varphi (v_0,v_1,v_2)$
. Let
![]() $\gamma _0 = \min (S)$
and
$\gamma _0 = \min (S)$
and
![]() $\gamma _1 = \min (S \setminus (\alpha _{\gamma _0}+1))$
. Clearly, we then have
$\gamma _1 = \min (S \setminus (\alpha _{\gamma _0}+1))$
. Clearly, we then have
![]() $\gamma _0<\gamma _1$
and
$\gamma _0<\gamma _1$
and
![]() $\alpha _{\gamma _1}> \alpha _{\gamma _0}$
. Let
$\alpha _{\gamma _1}> \alpha _{\gamma _0}$
. Let
![]() $G_0$
be
$G_0$
be
![]() $\mathbb {Q}(\gamma _0,{<}\kappa )$
-generic over V. As
$\mathbb {Q}(\gamma _0,{<}\kappa )$
-generic over V. As
![]() $\mathbb {Q}(\gamma _1,{<}\kappa )$
is a regular subforcing of
$\mathbb {Q}(\gamma _1,{<}\kappa )$
is a regular subforcing of
![]() $\mathbb {Q}(\gamma _0,{<}\kappa )$
, we can now find
$\mathbb {Q}(\gamma _0,{<}\kappa )$
, we can now find
![]() $G_1\in V[G_0]$
that is
$G_1\in V[G_0]$
that is
![]() $\mathbb {Q}(\gamma _1,{<}\kappa )$
-generic over V. In this situation, we know that
$\mathbb {Q}(\gamma _1,{<}\kappa )$
-generic over V. In this situation, we know that
![]() $\varphi (\alpha _{\gamma _1},\kappa ,x)$
holds in
$\varphi (\alpha _{\gamma _1},\kappa ,x)$
holds in
![]() $V[G_1]$
, and by
$V[G_1]$
, and by
![]() $\Sigma _1$
-upwards absoluteness, this statement also holds in
$\Sigma _1$
-upwards absoluteness, this statement also holds in
![]() $V[G_0]$
. But this yields a contradiction because
$V[G_0]$
. But this yields a contradiction because
![]() $\alpha _{\gamma _1}>\alpha _{\gamma _0}$
, and
$\alpha _{\gamma _1}>\alpha _{\gamma _0}$
, and
![]() $\alpha _{\gamma _0}$
is the unique element a of
$\alpha _{\gamma _0}$
is the unique element a of
![]() $V[G_0]$
with the property that
$V[G_0]$
with the property that
![]() $\varphi (a,\kappa ,x)$
holds in
$\varphi (a,\kappa ,x)$
holds in
![]() $V[G_0]$
.
$V[G_0]$
.
Proof of Theorem 5.11
Suppose that
![]() $\mu $
is a regular cardinal so that the set
$\mu $
is a regular cardinal so that the set
![]() $\{\mu \}$
is
$\{\mu \}$
is
![]() $\Sigma _1$
-stationary in
$\Sigma _1$
-stationary in
![]() $\mu ^+$
. Assume, toward a contradiction, that
$\mu ^+$
. Assume, toward a contradiction, that
![]() $\kappa =\mu ^+$
is not a Mahlo cardinal in
$\kappa =\mu ^+$
is not a Mahlo cardinal in
![]() $\mathrm {{L}}$
. Then, there is a constructible closed unbounded subset of
$\mathrm {{L}}$
. Then, there is a constructible closed unbounded subset of
![]() $\kappa $
whose elements are singular in
$\kappa $
whose elements are singular in
![]() $\mathrm {{L}}$
. Let C denote the
$\mathrm {{L}}$
. Let C denote the
![]() $<_{\mathrm {L}}$
-least such subset of
$<_{\mathrm {L}}$
-least such subset of
![]() $\kappa $
. Then, the set
$\kappa $
. Then, the set
![]() $\{C\}$
is definable by a
$\{C\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
, and hence, we know that
$\kappa $
, and hence, we know that
![]() $\mu $
is an element of C. But this is a contradiction because all elements of C are singular.
$\mu $
is an element of C. But this is a contradiction because all elements of C are singular.
The above computations yield the implication from (3) to (1) in the statement of the theorem. The implication from (1) to (2) is given by a combination of Lemma 2.12 and Lemma 5.12. Finally, the implication from (2) to (3) is trivial.
5.4 Successors of singular cardinals
The last arguments used in the above proof of Theorem 5.11 do not apply if we consider successors of singular cardinals. Indeed, it turns out that the corresponding assumption has much higher consistency strength. In one direction, we show that an analogous statement holds for successors of limits of measurable cardinals:
Theorem 5.13 If
![]() $\kappa $
is a limit of measurable cardinals, then the cardinal
$\kappa $
is a limit of measurable cardinals, then the cardinal
![]() $\kappa ^+$
has the
$\kappa ^+$
has the
![]() $\Sigma _1(\kappa )$
-undefinability property.
$\Sigma _1(\kappa )$
-undefinability property.
Proof Assume, toward a contradiction, that there is a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
, an ordinal
$\varphi (v_0,v_1,v_2)$
, an ordinal
![]() $\alpha $
in the interval
$\alpha $
in the interval
![]() $[\kappa ,\kappa ^+)$
, and an element z of
$[\kappa ,\kappa ^+)$
, and an element z of
![]() $\mathrm {H}_{\kappa }$
such that
$\mathrm {H}_{\kappa }$
such that
![]() $\alpha $
is the unique set a with the property that
$\alpha $
is the unique set a with the property that
![]() $\varphi (a,\kappa ^+,z)$
holds. Pick a measurable cardinal
$\varphi (a,\kappa ^+,z)$
holds. Pick a measurable cardinal
![]() $\delta <\kappa $
such that
$\delta <\kappa $
such that
![]() $z\in \mathrm {H}_{\delta }$
and
$z\in \mathrm {H}_{\delta }$
and
![]() ${\mathrm {{cof}}(\kappa )}\in \delta \cup \{\kappa \}$
. Pick a normal ultrafilter U on
${\mathrm {{cof}}(\kappa )}\in \delta \cup \{\kappa \}$
. Pick a normal ultrafilter U on
![]() $\delta $
, and let
$\delta $
, and let
denote the linear iteration of
![]() $\langle V,\in ,U\rangle $
. Standard arguments now allow us to conclude that
$\langle V,\in ,U\rangle $
. Standard arguments now allow us to conclude that
![]() $j_{0,\gamma }(\kappa ^+)=\kappa ^+$
and
$j_{0,\gamma }(\kappa ^+)=\kappa ^+$
and
![]() $j_{0,\gamma }(z)=z$
holds for all
$j_{0,\gamma }(z)=z$
holds for all
![]() $\gamma <\kappa ^+$
(see, for example, [Reference Lücke and Müller15, Lemma 7.3]). We can now pick
$\gamma <\kappa ^+$
(see, for example, [Reference Lücke and Müller15, Lemma 7.3]). We can now pick
![]() $\gamma <\kappa ^+$
with
$\gamma <\kappa ^+$
with
![]() $j_{0,\gamma }(\delta )>\alpha $
. Elementarity then implies that
$j_{0,\gamma }(\delta )>\alpha $
. Elementarity then implies that
![]() $\varphi (j_{0,\gamma }(\alpha ),\kappa ^+,z)$
holds in
$\varphi (j_{0,\gamma }(\alpha ),\kappa ^+,z)$
holds in
![]() $M_\gamma $
, and by
$M_\gamma $
, and by
![]() $\Sigma _1$
-upwards absoluteness, this shows that
$\Sigma _1$
-upwards absoluteness, this shows that
![]() $\varphi (j_{0,\gamma }(\alpha ),\kappa ^+,z)$
also holds in V. Since
$\varphi (j_{0,\gamma }(\alpha ),\kappa ^+,z)$
also holds in V. Since
![]() $j_{0,\gamma }(\alpha )>\alpha $
, this yields a contradiction.
$j_{0,\gamma }(\alpha )>\alpha $
, this yields a contradiction.
In combination with Lemma 2.12, the above result shows that if
![]() $\kappa $
is a limit of measurable cardinals, then the set
$\kappa $
is a limit of measurable cardinals, then the set
![]() $\{\kappa \}$
is
$\{\kappa \}$
is
![]() $\Sigma _1(\mathrm {H}_{\kappa })$
-stationary in
$\Sigma _1(\mathrm {H}_{\kappa })$
-stationary in
![]() $\kappa ^+$
. We end this section by showing that in the case of successors of singular cardinals, the used large cardinal assumption is optimal. In the proof of this result, we again rely on the results of [Reference Koepke11].
$\kappa ^+$
. We end this section by showing that in the case of successors of singular cardinals, the used large cardinal assumption is optimal. In the proof of this result, we again rely on the results of [Reference Koepke11].
Theorem 5.14 Let
![]() $\kappa $
be a singular cardinal with the property that the set
$\kappa $
be a singular cardinal with the property that the set
![]() $\{\kappa \}$
is
$\{\kappa \}$
is
![]() $\Sigma _1(\mathrm {H}_{\kappa })$
-stationary in
$\Sigma _1(\mathrm {H}_{\kappa })$
-stationary in
![]() $\kappa ^+$
. Then, there is an inner model with
$\kappa ^+$
. Then, there is an inner model with
![]() ${\mathrm {{cof}}(\kappa )}$
-many measurable cardinals.
${\mathrm {{cof}}(\kappa )}$
-many measurable cardinals.
Proof Assume, toward a contradiction, that the above conclusion fails. An application of [Reference Koepke11, Theorem 2.14] then shows that
![]() $0^{long}$
does not exist. Let
$0^{long}$
does not exist. Let
![]() $U_{can}$
denote the canonical sequence of measures, and let
$U_{can}$
denote the canonical sequence of measures, and let
![]() $\mathrm {{K}}[U_{can}]$
denote the canonical core model. Our assumption then implies that
$\mathrm {{K}}[U_{can}]$
denote the canonical core model. Our assumption then implies that
![]() ${\mathrm {{dom}}(U_{can}\restriction \kappa )}$
is a bounded subset of
${\mathrm {{dom}}(U_{can}\restriction \kappa )}$
is a bounded subset of
![]() $\kappa $
.
$\kappa $
.
Claim
![]() $\kappa ^+=(\kappa ^+)^{\mathrm {{K}}[U_{can}]}$
.
$\kappa ^+=(\kappa ^+)^{\mathrm {{K}}[U_{can}]}$
.
Proof of the Claim
First, if
![]() $\kappa \notin {\mathrm {{dom}}(U_{can})}$
, then the fact that
$\kappa \notin {\mathrm {{dom}}(U_{can})}$
, then the fact that
![]() ${\mathrm {{dom}}(U_{can}\restriction \kappa )}$
is bounded in
${\mathrm {{dom}}(U_{can}\restriction \kappa )}$
is bounded in
![]() $\kappa $
allows us to use [Reference Koepke11, Theorem 3.20] to derive the desired conclusion. Hence, we may assume that
$\kappa $
allows us to use [Reference Koepke11, Theorem 3.20] to derive the desired conclusion. Hence, we may assume that
![]() $\kappa $
is an element of
$\kappa $
is an element of
![]() ${\mathrm {{dom}}(U_{can})}$
. An application of [Reference Koepke11, Theorem 3.23] then shows that
${\mathrm {{dom}}(U_{can})}$
. An application of [Reference Koepke11, Theorem 3.23] then shows that
![]() ${\mathrm {{cof}}(\kappa )}=\omega $
, and there is a generic extension of
${\mathrm {{cof}}(\kappa )}=\omega $
, and there is a generic extension of
![]() $\mathrm {{K}}[U_{can}]$
by finitely-many Prikry forcings that computes
$\mathrm {{K}}[U_{can}]$
by finitely-many Prikry forcings that computes
![]() $\kappa ^+$
correctly. But this also means that
$\kappa ^+$
correctly. But this also means that
![]() $\mathrm {{K}}[U_{can}]$
computes
$\mathrm {{K}}[U_{can}]$
computes
![]() $\kappa ^+$
correctly.
$\kappa ^+$
correctly.
Set
![]() $U=U_{can}\restriction \kappa \in \mathrm {H}_{\kappa }$
. By [Reference Koepke11, Theorem 3.9], we then have
$U=U_{can}\restriction \kappa \in \mathrm {H}_{\kappa }$
. By [Reference Koepke11, Theorem 3.9], we then have
![]() ${\mathcal {P}}({\kappa })^{\mathrm {{K}}[U_{can}]}\subseteq \mathrm {{K}}[U]$
, and hence, the above claim shows that
${\mathcal {P}}({\kappa })^{\mathrm {{K}}[U_{can}]}\subseteq \mathrm {{K}}[U]$
, and hence, the above claim shows that
![]() $\kappa ^+=(\kappa ^+)^{\mathrm {{K}}[U]}$
.
$\kappa ^+=(\kappa ^+)^{\mathrm {{K}}[U]}$
.
Claim The set
![]() $\{\kappa \}$
is definable by a
$\{\kappa \}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\kappa ^+$
and U.
$\kappa ^+$
and U.
Proof of the Claim
If
![]() $\zeta <\kappa ^+$
is an ordinal and M is a U-mouse (i.e., an iterable premouse over U; see [Reference Koepke11, Definition 2.5]) with
$\zeta <\kappa ^+$
is an ordinal and M is a U-mouse (i.e., an iterable premouse over U; see [Reference Koepke11, Definition 2.5]) with
![]() $\kappa ^+\in lp(M)$
and
$\kappa ^+\in lp(M)$
and
![]() $\kappa ^+=(\zeta ^+)^M$
, then a direct adaptation of the proof of Lemma 3.1 shows that
$\kappa ^+=(\zeta ^+)^M$
, then a direct adaptation of the proof of Lemma 3.1 shows that
![]() ${\mathcal {P}}({\kappa })\subseteq M$
, and hence,
${\mathcal {P}}({\kappa })\subseteq M$
, and hence,
![]() $\kappa =\zeta $
. Since there exists a U-mouse that satisfies the listed properties with respect to
$\kappa =\zeta $
. Since there exists a U-mouse that satisfies the listed properties with respect to
![]() $\kappa $
, this observation yields the desired definition of the set
$\kappa $
, this observation yields the desired definition of the set
![]() $\{\kappa \}$
.
$\{\kappa \}$
.
The above claim directly yields a contradiction because it implies that the set
![]() $\{(\kappa ,\kappa ^+)\}$
is definable by a
$\{(\kappa ,\kappa ^+)\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\kappa }\cup \{\kappa ^+\}$
.
$\mathrm {H}_{\kappa }\cup \{\kappa ^+\}$
.
6 Open Problems
There are many natural ways to vary Definition 2.2. For example, given a cardinal
![]() $\kappa $
greater than
$\kappa $
greater than
![]() $\omega _1$
, we may ask whether for some uncountable ordinal
$\omega _1$
, we may ask whether for some uncountable ordinal
![]() $\alpha <\kappa $
, the set
$\alpha <\kappa $
, the set
![]() $\{\alpha \}$
is definable by a
$\{\alpha \}$
is definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\kappa $
. Since our arguments to derive consistency strength from the undefinability property (as in the proof of Theorem 5.3) cannot be directly adjusted to this variation, we arrive at the following question:
$\kappa $
. Since our arguments to derive consistency strength from the undefinability property (as in the proof of Theorem 5.3) cannot be directly adjusted to this variation, we arrive at the following question:
Question 6.1 Assume that for every uncountable ordinal
![]() $\alpha <\omega _\omega $
, the set
$\alpha <\omega _\omega $
, the set
![]() $\{\alpha \}$
is not definable by a
$\{\alpha \}$
is not definable by a
![]() $\Sigma _1$
-formula with parameter
$\Sigma _1$
-formula with parameter
![]() $\omega _\omega $
. Does
$\omega _\omega $
. Does
![]() $0^\#$
exist?
$0^\#$
exist?
In Section 4.3, we show that many of the implications of large cardinals on
![]() $\Sigma _1(A)$
-stationary sets can also be derived for smaller cardinals in the case where these cardinals possess strong partition properties. For some of these implications, it is natural to ask whether they can be strengthened. First, since Lemma 4.12 relies on additional assumptions on the given Rowbottom cardinal, we ask whether these assumptions can be omitted:
$\Sigma _1(A)$
-stationary sets can also be derived for smaller cardinals in the case where these cardinals possess strong partition properties. For some of these implications, it is natural to ask whether they can be strengthened. First, since Lemma 4.12 relies on additional assumptions on the given Rowbottom cardinal, we ask whether these assumptions can be omitted:
Question 6.2 Does every
![]() $\mu $
-Rowbottom cardinal have the
$\mu $
-Rowbottom cardinal have the
![]() $\Sigma _1(\mu )$
-undefinability property?
$\Sigma _1(\mu )$
-undefinability property?
Second, when we consider
![]() $\Sigma _1$
-definable regressive functions and compare the third part of Theorem 4.1 and the second part of Theorem 4.6 with the second part of Theorem 4.13, then we notice that our result for the case where
$\Sigma _1$
-definable regressive functions and compare the third part of Theorem 4.1 and the second part of Theorem 4.6 with the second part of Theorem 4.13, then we notice that our result for the case where
![]() $\omega _\omega $
is Jónsson is restricted to
$\omega _\omega $
is Jónsson is restricted to
![]() $\boldsymbol {\Sigma }_1$
-stationary sets consisting of cardinals. We therefore ask if the given conclusion can also be extended to arbitrary
$\boldsymbol {\Sigma }_1$
-stationary sets consisting of cardinals. We therefore ask if the given conclusion can also be extended to arbitrary
![]() $\boldsymbol {\Sigma }_1$
-stationary subsets in this setting.
$\boldsymbol {\Sigma }_1$
-stationary subsets in this setting.
Question 6.3 Assume that
![]() $\omega _\omega $
is a Jónsson cardinal, S is a
$\omega _\omega $
is a Jónsson cardinal, S is a
![]() $\boldsymbol {\Sigma }_1$
-stationary subset of
$\boldsymbol {\Sigma }_1$
-stationary subset of
![]() $\omega _\omega $
, and
$\omega _\omega $
, and
![]() ${r}:{\omega _\omega }\longrightarrow {\omega _\omega }$
is a regressive function that is definable by a
${r}:{\omega _\omega }\longrightarrow {\omega _\omega }$
is a regressive function that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $\mathrm {H}_{\aleph _\omega }\cup \{\omega _\omega \}$
. Is r constant on a
$\mathrm {H}_{\aleph _\omega }\cup \{\omega _\omega \}$
. Is r constant on a
![]() $\boldsymbol {\Sigma }_1$
-stationary subset of S?
$\boldsymbol {\Sigma }_1$
-stationary subset of S?
Finally, let us say that a cardinal
![]() $\kappa $
is strongly measurable with respect to
$\kappa $
is strongly measurable with respect to
![]() $\Sigma _1(\mathrm{Ord})$
-clubs if there is an inner model W in which
$\Sigma _1(\mathrm{Ord})$
-clubs if there is an inner model W in which
![]() $\kappa $
is measurable such that the collection of
$\kappa $
is measurable such that the collection of
![]() $\Sigma _1(\mathrm{Ord})$
-closed unbounded subsets of
$\Sigma _1(\mathrm{Ord})$
-closed unbounded subsets of
![]() $\kappa $
(in V) is generated by the intersection filter
$\kappa $
(in V) is generated by the intersection filter
![]() $F \in W$
of
$F \in W$
of
![]() $\eta < \kappa $
many
$\eta < \kappa $
many
![]() $\kappa $
-complete ultrafilters on
$\kappa $
-complete ultrafilters on
![]() $\kappa $
in W. The proof of Theorem 5.3 shows that
$\kappa $
in W. The proof of Theorem 5.3 shows that
![]() $\omega _\omega $
can be strongly measurable with respect to
$\omega _\omega $
can be strongly measurable with respect to
![]() $\Sigma _1$
-definable clubs. Can the same hold for other singular cardinals such as
$\Sigma _1$
-definable clubs. Can the same hold for other singular cardinals such as
![]() $\omega _{\omega _1}$
?
$\omega _{\omega _1}$
?
Question 6.4 Can
![]() $\omega _{\omega _1}$
be strongly measurable with respect to
$\omega _{\omega _1}$
be strongly measurable with respect to
![]() $\Sigma _1(\mathrm{Ord})$
-clubs?
$\Sigma _1(\mathrm{Ord})$
-clubs?
See [Reference Ben-Neria and Unger3] for an analog of Prikry forcing, that changes the cofinality of a cardinal
![]() $\kappa $
to
$\kappa $
to
![]() $\omega _1$
by a homogeneous poset.
$\omega _1$
by a homogeneous poset.
Acknowledgements
The authors would like to thank Matt Foreman, Yair Hayut, and Menachem Magidor for their comments, and an anonymous referee for valuable suggestions and comments.