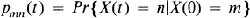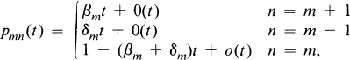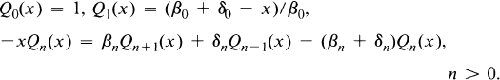Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nevai, Paul
1986.
Géza Freud, orthogonal polynomials and Christoffel functions. A case study.
Journal of Approximation Theory,
Vol. 48,
Issue. 1,
p.
3.
Ismail, Mourad E.H
1986.
On sieved orthogonal polynomials. IV. Generating functions.
Journal of Approximation Theory,
Vol. 46,
Issue. 3,
p.
284.
Ismail, Mourad E. H.
1986.
On sieved orthogonal polynomials. III. Orthogonality on several intervals.
Transactions of the American Mathematical Society,
Vol. 294,
Issue. 1,
p.
89.
Charris, Jairo A.
and
Ismail, Mourad E. H.
1987.
On Sieved Orthogonal Polynomials. V: Sieved Pollaczek Polynomials.
SIAM Journal on Mathematical Analysis,
Vol. 18,
Issue. 4,
p.
1177.
Geronimo, J. S.
and
Van Assche, W.
1988.
Orthogonal polynomials on several intervals via a polynomial mapping.
Transactions of the American Mathematical Society,
Vol. 308,
Issue. 2,
p.
559.
Van Assche, Walter
and
Magnus, Alphonse P.
1989.
Sieved orthogonal polynomials and discrete measures with jumps dense in an interval.
Proceedings of the American Mathematical Society,
Vol. 106,
Issue. 1,
p.
163.
Al-Salam, Nadhla A
and
Ismail, Mourad E.H
1992.
On sieved orthogonal polynomials. VIII. Sieved associated Pollaczek polynomials.
Journal of Approximation Theory,
Vol. 68,
Issue. 3,
p.
306.
Gautschi, Walter
and
Li, Shikang
1993.
A set of orthogonal polynomials induced by a given orthogonal polynomial.
Aequationes Mathematicae,
Vol. 46,
Issue. 1-2,
p.
174.
Charris, Jairo A.
and
Ismail, Mourad E. H.
1993.
Sieved orthogonal polynomials. VII. Generalized polynomial mappings.
Transactions of the American Mathematical Society,
Vol. 340,
Issue. 1,
p.
71.
Dette, Holger
1996.
Characterizations of generalized Hermite and sieved ultraspherical polynomials.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 2,
p.
691.
Coolen-Schrijner, Pauline
and
van Doorn, Erik A.
1998.
Analysis of random walks using orthogonal polynomials.
Journal of Computational and Applied Mathematics,
Vol. 99,
Issue. 1-2,
p.
387.
Desesa, Blaise
1998.
Orthogonality of Sieved Random Walk Polynomials from a Nonsieved Analogue.
SIAM Journal on Mathematical Analysis,
Vol. 29,
Issue. 1,
p.
251.
Osilenker, Boris P.
1998.
Lie Groups and Lie Algebras.
p.
147.
Osilenker, B.
1998.
An analog of the trace formula for orthogonal polynomials with asymptoticallyN-periodic recurrence coefficients (N=2).
Analysis Mathematica,
Vol. 24,
Issue. 1,
p.
293.
Masjed-Jamei, Mohammad
2007.
A basic class of symmetric orthogonal polynomials using the extended Sturm–Liouville theorem for symmetric functions.
Journal of Mathematical Analysis and Applications,
Vol. 325,
Issue. 2,
p.
753.
Chen, Yang
Griffin, James
and
Ismail, Mourad
2007.
Generalizations of Chebyshev polynomials and polynomial mappings.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 10,
p.
4787.
Castillo, K.
de Jesus, M. N.
and
Petronilho, J.
2020.
An electrostatic interpretation of the zeros of sieved ultraspherical polynomials.
Journal of Mathematical Physics,
Vol. 61,
Issue. 5,
Ismail, Mourad E. H.
and
Assche, Walter Van
2020.
Encyclopedia of Special Functions: The Askey-Bateman Project.
Castillo, K.
de Jesus, M.N.
and
Petronilho, J.
2021.
A note on orthogonal polynomials described by Chebyshev polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 497,
Issue. 2,
p.
124906.
Tefo, Yves Guemo
Aktaş, Rabia
Area, Iván
and
Güldoğan Lekesiz, Esra
2022.
On a Symmetric Generalization of Bivariate Sturm–Liouville Problems.
Bulletin of the Iranian Mathematical Society,
Vol. 48,
Issue. 4,
p.
1649.