Article contents
On Representations as a Sum of Consecutive Integers
Published online by Cambridge University Press: 20 November 2018
Extract
1. Introduction. It is the object of this paper to investigate the function γ(m), the number of representations of m in the form
(1) 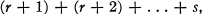
where 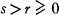 . It is shown that γ(m) is always equal to the number of odd divisors of m, so that for example γ(2k) = 1, this representation being the number 2k itself. From this relationship the average order of γ(m) is deduced ; this result is given in Theorem 2. By a method due to Kac [2], it is shown in §3 that the number of positive integers
. It is shown that γ(m) is always equal to the number of odd divisors of m, so that for example γ(2k) = 1, this representation being the number 2k itself. From this relationship the average order of γ(m) is deduced ; this result is given in Theorem 2. By a method due to Kac [2], it is shown in §3 that the number of positive integers 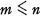 for which γ(m) does not exceed a rather complicated function of n and ω, a real parameter, is asymptotically nD(ω), where D(ω) is the probability integral
for which γ(m) does not exceed a rather complicated function of n and ω, a real parameter, is asymptotically nD(ω), where D(ω) is the probability integral
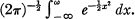
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1950
References
- 11
- Cited by


