Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T13:26:26.840Z Has data issue: false hasContentIssue false
  • English
  • Français

On Reducibility and Unitarizability for Classical p-Adic Groups, Some General Results

Published online by Cambridge University Press:  20 November 2018

Marko Tadić
Marko Tadić*
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička 30, 10000 Zagreb, Croatia, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

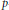The aim of this paper is to prove two general results on parabolic induction of classical $p$-adic groups (actually, one of them holds also in the archimedean case), and to obtain from them some consequences about irreducible unitarizable representations. One of these consequences is a reduction of the unitarizability problem for these groups. This reduction is similar to the reduction of the unitarizability problem to the case of real infinitesimal character for real reductive groups.

Keywords

22E5022E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 427 - 450
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Ban, D. and Jantzen, C., R-groups and the action of intertwining operators in the nontempered case. Int. Math. Res. Not. IMRN 2007, no. 20, Art. ID rnm059.Google Scholar
[2] Bernstein, J., P-invariant distributions on GL (N ) and the classification of unitary representations of GL (N ) (non-Archimedean case). In: Lie group representations II, Lecture Notes in Mathematics 1041, Springer-Verlag, Berlin, 1984, pp. 50–102.Google Scholar
[3] Barbasch, D. and Moy, A., Reduction to real infinitesimal character in affine Hecke algebras. J. Amer. Math. Soc. 6(1993), no. 3, 611–635.Google Scholar
[4] Casselman, W., Introduction to the theory of admissible representations of p-adic reductive groups. preprint. http://www.math.ubc.ca/~cass/research/pdf/p-adic-book. pdfGoogle Scholar
[5] Goldberg, D., Reducibility of induced representations for Sp (2n ) and SO (n . Amer. J. Math. 116(1994), no. 5, 1101–1151.Google Scholar
[6] Hanzer, M., R groups for quaternionic Hermitian groups. Glas. Mat. 39(59)(2004), no. 1, 31–48.Google Scholar
[7] Jantzen, C., On supports of induced representations for symplectic and odd-orthogonal groups. Amer J. Math. 119(1997), no. 6, 1213–1262.Google Scholar
[8] Moeglin, C., Sur la classification des séries discrètes des groupes classiques p-adiques: paramètres de Langlands et exhaustivité. J. Eur. Math. Soc. 4(2002), no. 2, 143–200.Google Scholar
[9] Moeglin, C. and Tadić, M., Construction of discrete series for classical p-adic groups. J. Amer. Math. Soc. 15(2002), no. 3, 715–786.Google Scholar
[10] Muic, G., Reducibility of generalized principal series. Canad. J. Math. 57(2005), no. 3, 616–647.Google Scholar
[11] Muic, G., Reducibility of standard representations. Pacific. J. Math. 222(2005), no. 1, 133–168.Google Scholar
[12] Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Math. 132(1990), no. 2, 273–330.Google Scholar
[13] Shahidi, F., Twisted endoscopy and reducibility of induced representations for p-adic groups. Duke Math. J. 66(1992), no. 1, 1–41.Google Scholar
[14] Tadić, M., Classification of unitary representations in irreducible representations of general linear group (non-Archimedean case). Ann. Sci. École Norm. Sup. 19(1986), no. 3, 335–382.Google Scholar
[15] Tadić, M., GL (n , C)ˆand GL (n , R)ˆ. To appear in a workshop in honor of S. Gelbart on Automorphic Forms and L-functions. http://www.hazu/~tadic/42-GL-arch.pdf.Google Scholar
[16] Tadić, M., Geometry of dual spaces of reductive groups (non-Archimedean case). J. Analyse Math. 51(1988), 139–181.Google Scholar
[17] Tadić, M., Structure arising from induction and Jacquet modules of representations of classical p-adic groups. J. Algebra 177(1995), no. 1, 1–33.Google Scholar
[18] Tadić, M., Representations of p-adic symplectic groups. Compositio Math. 90(1994), no. 2, 123–181.Google Scholar
[19] Tadić, M., An external approach to unitary representations. Bull. Amer. Math. Soc. 28(1993), no. 2, 212–252.Google Scholar
[20] Tadić, M., On reducibility of parabolic induction. Israel J. Math. 107(1998), 29–91.Google Scholar
[21] Tadić, M., On regular square integrable representations of p-adic groups. Amer. J. Math. 120(1998), no. 1, 159–210.Google Scholar
[22] Tadić, M., On classification of some classes of irreducible representations of classical groups. In: Representations of real and p -adic groups, Lect. Notes Ser. Inst. Math. Sci. Natl. Singap. 2, Singapore University Press and World Scientific, Singapore, 1994, pp. 95–162.Google Scholar
[23] Zelevinsky, A. V., Induced representations of reductive p-adic groups II. On irreducible representations of GL (n . Ann. Sci. École Norm. Sup. 13(1980), no. 2, 165–210.Google Scholar