Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mundici, D.
2011.
Advanced Łukasiewicz calculus and MV-algebras.
p.
187.
CABRER, LEONARDO
and
MUNDICI, DANIELE
2012.
RATIONAL POLYHEDRA AND PROJECTIVE LATTICE-ORDERED ABELIAN GROUPS WITH ORDER UNIT.
Communications in Contemporary Mathematics,
Vol. 14,
Issue. 03,
p.
1250017.
Cabrer, Leonardo Manuel
and
Mundici, Daniele
2015.
Severi–Bouligand tangents, Frenet frames and Riesz spaces.
Advances in Applied Mathematics,
Vol. 64,
Issue. ,
p.
1.
Mundici, Daniele
2016.
On Logical, Algebraic, and Probabilistic Aspects of Fuzzy Set Theory.
Vol. 336,
Issue. ,
p.
57.
Cabrer, Leonardo Manuel
and
Mundici, Daniele
2017.
Idempotent endomorphisms of free MV-algebras and unital ℓ-groups.
Journal of Pure and Applied Algebra,
Vol. 221,
Issue. 4,
p.
908.
Mundici, Daniele
2020.
Fields of Logic and Computation III.
Vol. 12180,
Issue. ,
p.
210.
ADAM-DAY, SAM
BEZHANISHVILI, NICK
GABELAIA, DAVID
and
MARRA, VINCENZO
2024.
POLYHEDRAL COMPLETENESS OF INTERMEDIATE LOGICS: THE NERVE CRITERION.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 1,
p.
342.


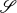 is a simplicial subdivision of
is a simplicial subdivision of