Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:44:15.614Z Has data issue: false hasContentIssue false
  • English
  • Français

On Pointwise Estimates of Positive Definite Functions With Given Support

Published online by Cambridge University Press:  20 November 2018

Mihail N. Kolountzakis  and
Szilárd Gy. Révész
Mihail N. Kolountzakis
Affiliation:
Department of Mathematics, University of Crete, Knossos Ave. 714 09 Iraklio, Greece e-mail: [email protected]
Szilárd Gy. Révész
Affiliation:
Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences, 1364 Budapest, Hungary e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following problem has been suggested by Paul Turán. Let 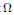$\Omega $ be a symmetric convex body in the Euclidean space 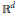${{\mathbb{R}}^{d}}$ or in the torus 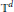${{\mathbb{T}}^{d}}$. Then, what is the largest possible value of the integral of positive definite functions that are supported in 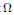$\Omega $ and normalized with the value 1 at the origin? From this, Arestov, Berdysheva and Berens arrived at the analogous pointwise extremal problem for intervals in 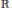$\mathbb{R}$. That is, under the same conditions and normalizations, the supremum of possible function values at 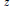$z$ is to be found for any given point 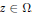$z\,\in \,\Omega $. However, it turns out that the problem for the real line has already been solved by Boas and Kac, who gave several proofs and also mentioned possible extensions to 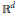${{\mathbb{R}}^{d}}$ and to non-convex domains as well.

Here we present another approach to the problem, giving the solution in 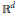${{\mathbb{R}}^{d}}$ and for several cases in 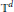${{\mathbb{T}}^{d}}$. Actually, we elaborate on the fact that the problem is essentially one-dimensional and investigate non-convex open domains as well. We show that the extremal problems are equivalent to some more familiar ones concerning trigonometric polynomials, and thus find the extremal values for a few cases. An analysis of the relationship between the problem for 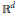${{\mathbb{R}}^{d}}$ and that for 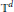${{\mathbb{T}}^{d}}$ is given, showing that the former case is just the limiting case of the latter. Thus the hierarchy of difficulty is established, so that extremal problems for trigonometric polynomials gain renewed recognition.

Keywords

42B1026D1542A8242A05Fourier transformpositive definite functions and measuresTurán's extremal problemconvex symmetric domainspositive trigonometric polynomialsdual extremal problems
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 2 , 01 April 2006 , pp. 401 - 418
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Arestov, V. and Berdysheva, E., The Turán problem for a class of polytopes. East J. Approx. 8(2002), no. 3, 381–388.Google Scholar
[2] Arestov, V., Berdysheva, E., and Berens, H., On pointwise Turán's problem for positive definite functions. East J. Approx. 9(2003), no. 1, 31–42.Google Scholar
[3] Boas, R. P. Jr. and Kac, M., Inequalities for Fourier Transforms of positive functions. Duke Math. J. 12(1945), 189–206.Google Scholar
[4]C. Carathéodory, Über den Variabilitätsbereich der Fourier’schen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo 32(1911), 193–217.Google Scholar
[5] Fejér, L., Über trigonometrische Polynome. J. Angew.Math. 146(1915), 53–82.Google Scholar
[6] Fejér, L., Gesammelte Arbeiten I-II, Akadémiai Kiadó, Budapest, 1970.Google Scholar
[7] Gorbachev, D. V. and Manoshina, A. S. The extremal Turán problem for periodic functions with small supports. Chebyshevskii Sb. 2(2001), 31–40 (in Russian).Google Scholar
[8] Gorbachev, D. V. and Manoshina, A. S., The Turán extremal problem for periodic functions with small support and its applications. Math. Notes 76(2004), no. 5-6, 640–652.Google Scholar
[9] Kolountzakis, M. and Révész, Sz., On a problem of Turán about positive definite functions. Proc. Amer.Math. Soc. 131(2003), no. 11, 3423–3430.Google Scholar
[10] Konyagin, S. and Shparlinski, I., Character sums with exponential functions and their applications. Cambridge Tracts in Mathematics 136, Cambridge University Press, Cambridge, 1999.Google Scholar
[11] Pólya, G. and Szegö, G., Problems and Theorems in Analysis II, Springer-Verlag, Berlin, 1998.Google Scholar
[12] Révész, Sz. Gy., Extremal problems and a duality phenomenon. In: Approximation, Optimization and Computing, North Holland, Amsterdam, 1990, pp. 279–281.Google Scholar
[13] Révész, Sz. Gy., A Fejér-type extremal problem, Acta Math. Hung. 57(1991) no. 3-4, 279–283.Google Scholar
[14] Révész, Sz. Gy., On Beurling's prime number theorem. Period. Math. Hungar 28(1994), no. 3, 195–210.Google Scholar
[15] Révész, Sz. Gy., The least possible value at zero of some nonnegative cosine polynomials and equivalent dual problems. J. Fourier Anal. Appl. Special Issue(1995), 485–508.Google Scholar
[16] Schönberg, I. J., Some extremal problems for positive definite sequences and related extremal convex conformal maps of the circle. Indag. Math. 20(1958), 28–37.Google Scholar
[17] Stechkin, S. B., An extremal problem for trigonometric series with nonnegative coefficients. Acta Math. Acad. Sci. Hung. 23(1972), 289–291 (in Russian).Google Scholar