Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
CHEN, GOONG
NI, WEI-MING
PERRONNET, ALAIN
and
ZHOU, JIANXIN
2001.
ALGORITHMS AND VISUALIZATION FOR SOLUTIONS OF NONLINEAR ELLIPTIC EQUATIONS, PART II: DIRICHLET, NEUMANN AND ROBIN BOUNDARY CONDITIONS AND PROBLEMS IN 3D.
International Journal of Bifurcation and Chaos,
Vol. 11,
Issue. 07,
p.
1781.
Malchiodi, Andrea
and
Montenegro, Marcelo
2002.
Boundary concentration phenomena for a singularly perturbed elliptic problem.
Communications on Pure and Applied Mathematics,
Vol. 55,
Issue. 12,
p.
1507.
Bates, Peter W.
and
Shi, Junping
2002.
Existence and instability of spike layer solutions to singular perturbation problems.
Journal of Functional Analysis,
Vol. 196,
Issue. 2,
p.
211.
del Pino, Manuel
Kowalczyk, Michał
and
Wei, Juncheng
2003.
Multi-bump ground states of the Gierer–Meinhardt system in ℝ2.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 20,
Issue. 1,
p.
53.
Papacharalampous, I. E.
Kevrekidis, P. G.
Malomed, B. A.
and
Frantzeskakis, D. J.
2003.
Soliton collisions in the discrete nonlinear Schrödinger equation.
Physical Review E,
Vol. 68,
Issue. 4,
Rey, Olivier
and
Wei, Juncheng
2004.
Blowing up solutions for an elliptic Neumann problem with sub- or supercritical nonlinearity Part I: N=3.
Journal of Functional Analysis,
Vol. 212,
Issue. 2,
p.
472.
Malchiodi, Andrea
2004.
Solutions concentrating at curves for some singularly perturbed elliptic problems.
Comptes Rendus. Mathématique,
Vol. 338,
Issue. 10,
p.
775.
Malchiodi, Andrea
and
Montenegro, Marcelo
2004.
Multidimensional boundary layers for a singularly perturbed Neumann problem.
Duke Mathematical Journal,
Vol. 124,
Issue. 1,
WEI, JUNCHENG
and
WINTER, MATTHIAS
2004.
ON THE GIERER–MEINHARDT SYSTEM WITH SATURATION.
Communications in Contemporary Mathematics,
Vol. 06,
Issue. 02,
p.
259.
Ni, Wei-Ming
2004.
Vol. 1,
Issue. ,
p.
157.
D'Aprile, Teresa
and
Wei, Juncheng
2005.
On Bound States Concentrating on Spheres for the Maxwell--Schrödinger Equation.
SIAM Journal on Mathematical Analysis,
Vol. 37,
Issue. 1,
p.
321.
Li, Yi
and
Zhao, Chunshan
2005.
On the structure of solutions to a class of quasilinear elliptic Neumann problems.
Journal of Differential Equations,
Vol. 212,
Issue. 1,
p.
208.
Ni, Wei-Ming
Wei, Juncheng
and
Malchiodi, A.
2005.
Multiple clustered layer solutions for semilinear Neumann problems on a ball.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 22,
Issue. 2,
p.
143.
Wei, Juncheng
and
Winter, Matthias
2005.
Clustered spots in the FitzHugh–Nagumo system.
Journal of Differential Equations,
Vol. 213,
Issue. 1,
p.
121.
Ren, Xiaofeng
and
Wei, Juncheng
2005.
Nucleation in the FitzHugh–Nagumo system: Interface–spike solutions.
Journal of Differential Equations,
Vol. 209,
Issue. 2,
p.
266.
Lin, Tai-Chia
and
Wei, Juncheng
2005.
Spikes in two coupled nonlinear Schrödinger equations.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 22,
Issue. 4,
p.
403.
Lin, Tai-Chia
and
Wei, Juncheng
2005.
Ground State of N Coupled Nonlinear Schr�dinger Equations in Rn,n?3.
Communications in Mathematical Physics,
Vol. 255,
Issue. 3,
p.
629.
Rey, Olivier
and
Wei, Juncheng
2005.
Blowing up solutions for an elliptic Neumann problem with sub- or supercritical nonlinearity. Part II: \( N\geq4 \).
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 22,
Issue. 4,
p.
459.
Wei, Juncheng
and
Weth, Tobias
2005.
On the number of nodal solutions to a singularly perturbed Neumann problem.
manuscripta mathematica,
Vol. 117,
Issue. 3,
p.
333.
Wei, Juncheng
and
Winter, Matthias
2006.
Standing waves in the FitzHugh-Nagumo system and a problem in combinatorial geometry.
Mathematische Zeitschrift,
Vol. 254,
Issue. 2,
p.
359.
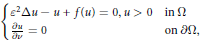 $$\left\{ \begin{matrix} {{\varepsilon }^{2}}\Delta u-u+f(u)=0,u>0 & \text{in}\,\Omega \\ \frac{\partial u}{\partial v}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & \text{on}\,\partial \Omega , \\\end{matrix} \right.$$
$$\left\{ \begin{matrix} {{\varepsilon }^{2}}\Delta u-u+f(u)=0,u>0 & \text{in}\,\Omega \\ \frac{\partial u}{\partial v}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, & \text{on}\,\partial \Omega , \\\end{matrix} \right.$$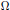 $\Omega $ is a bounded smooth domain in
$\Omega $ is a bounded smooth domain in 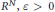 ${{R}^{N}},\varepsilon >0$ is a small parameter and
${{R}^{N}},\varepsilon >0$ is a small parameter and 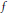 $f$ is a superlinear, subcritical nonlinearity. It is known that this equation possesses multiple boundary spike solutions that concentrate, as
$f$ is a superlinear, subcritical nonlinearity. It is known that this equation possesses multiple boundary spike solutions that concentrate, as  $\varepsilon $ approaches zero, at multiple critical points of the mean curvature function
$\varepsilon $ approaches zero, at multiple critical points of the mean curvature function 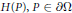 $H(P),P\in \partial \Omega $. It is also proved that this equation has multiple interior spike solutions which concentrate, as
$H(P),P\in \partial \Omega $. It is also proved that this equation has multiple interior spike solutions which concentrate, as 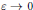 $\varepsilon \to 0$, at sphere packing points in
$\varepsilon \to 0$, at sphere packing points in 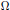 $\Omega $.
$\Omega $.

