Published online by Cambridge University Press: 20 November 2018
This paper forms a continuation of (1), extending the concept of a meromorphic operator to not necessarily bounded, closed linear operators in complex Banach space. Let T denote such an operator with range and domain in Banach space X. We shall study the class of such operators T where λ = 0 and λ = ∞ are the only allowable points of accumulation of σ(T) and every isolated point of σ(T) is a pole of Rλ(T). We shall write 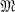 (0, ∞) to represent the class of such operators. If λ = 0 (λ = ∞) is the only allowable point of accumulation of σ(T), we shall write
(0, ∞) to represent the class of such operators. If λ = 0 (λ = ∞) is the only allowable point of accumulation of σ(T), we shall write 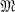 (0) (
(0) (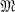 (∞)) to denote the corresponding class of operators.
(∞)) to denote the corresponding class of operators.