Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-08T11:26:31.040Z Has data issue: false hasContentIssue false
  • English
  • Français

On Major and Minor Branches of Rooted Trees

Published online by Cambridge University Press:  20 November 2018

A. Meir  and
J. W. Moon
A. Meir
Affiliation:
University of Alberta, Edmonton, Alberta
J. W. Moon
Affiliation:
University of Stirling, Stirling, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 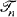denote a rooted tree with n nodes. (For definitions not given here, see, e.g. [4]). For any node v of 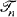, let B(v) denote the subtree of 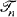determined by v and all nodes u such that v is between u and the root of 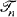; node v serves as the root of B(v). The branches of 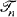are the subtrees B(v) such that node v is joined to the root of 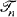. A branch B with i nodes is a primary branch of 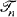if n/2 ≦ i ≦ n – 1; if 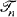has a primary branch B with i nodes, then a branch C with j nodes is a secondary branch if (n – i)/2 ≦ j ≦ n – 1 ≦ i; if 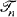has a primary branch B with i nodes and a secondary branch C with j nodes, then a branch D with h nodes is a tertiary branch if

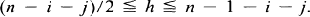
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 3 , 01 June 1987 , pp. 673 - 693
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Bromwich, T., An introduction to the theory of infinite series (Macmillan, London, 1931).Google Scholar
2. Darboux, G., Mémoire sur l'approximation des fonctions de très grands nombres, et sur une classe étendu de développements en série, J. Math. Pures et Appliquées 4 (1878), 5–56.Google Scholar
3. Flajolet, P. and Odlyzko, A., The average height of binary trees and other simple trees, J. Comput. System Sci. 25 (1982), 171–213.Google Scholar
4. Harary, F. and Palmer, E., Graphical enumeration (Academic Press, New York, 1973).Google Scholar
5. Hayman, W. K., A generalization of Stirling's formula, J. Reine Angew. Math. 196 (1956), 67–95.Google Scholar
6. Jordan, C., Sur les assemblages de lignes, J. Reine Angew Math. 79 (1869), 185–196.Google Scholar
7. Meir, A. and Moon, J. W., On the altitude of nodes in random trees, Can. J. Math. 39 (1978), 997–1015.Google Scholar
8. Meir, A. and Moon, J. W., Terminal path numbers for certain families of trees, J. Austral. Math. Soc. A31 (1981), 429–438.Google Scholar
9. Meir, A. and Moon, J. W., The outer-distance of nodes in random trees, Aequationes Math. 23 (1981), 204–211.Google Scholar
10. Meir, A., Moon, J. W. and Myceilski, J., Hereditarily finite sets and identity trees, J. Comb. Th. B 35(1983), 142–155.Google Scholar
11. Meir, A. and Moon, J. W., Games on random trees, Cong. Numer. 44 (1984), 293–303.Google Scholar
12. Otter, R., The number of trees, Ann. Math. 49 (1948), 583–599.Google Scholar