Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Andrunakievich, V. A.
Arnautov, V. I.
Goyan, I. M.
and
Ryabukhin, Yu. M.
1980.
Associative rings.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 1,
p.
922.
de Barros, Luiz G. X.
1993.
On sernisimple alternative loop algebras.
Communications in Algebra,
Vol. 21,
Issue. 11,
p.
3995.
de Barros, Luiz G. X.
and
Polcino Milies, César
1995.
Loop algebras of code loops.
Communications in Algebra,
Vol. 23,
Issue. 13,
p.
4781.
1996.
Alternative Loop Rings.
Vol. 184,
Issue. ,
p.
333.


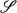 is a
is a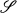
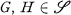
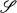 if they induce the same equivalence relation on
if they induce the same equivalence relation on  We will say
We will say  if
if  .
.