Article contents
On Implicational Completeness
Published online by Cambridge University Press: 20 November 2018
Extract
A class 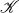 of (universal) algebras [4; 5] of the same type or species τ is called equationally complete if the variety [4] Var(
of (universal) algebras [4; 5] of the same type or species τ is called equationally complete if the variety [4] Var(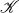 ) generated by
) generated by 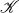 has exactly two subvarieties —namely Var(
has exactly two subvarieties —namely Var(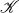 ) itself and the class of all one element algebras. I t follows that equationally complete varieties are the atoms in the complete lattice of all varieties of a given type of algebras. J. Kalicki, D. Scott [7; 8; 9; 10] and others [2; 3; 6; 12] have considered several questions about equational completeness. A good many of these results have appeared in books. (See, for instance, [4, 5], to which we also refer the reader for more extensive bibliography on subjects related to equational completeness.)
) itself and the class of all one element algebras. I t follows that equationally complete varieties are the atoms in the complete lattice of all varieties of a given type of algebras. J. Kalicki, D. Scott [7; 8; 9; 10] and others [2; 3; 6; 12] have considered several questions about equational completeness. A good many of these results have appeared in books. (See, for instance, [4, 5], to which we also refer the reader for more extensive bibliography on subjects related to equational completeness.)
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974
References
- 8
- Cited by


