Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T11:34:46.870Z Has data issue: false hasContentIssue false
  • English
  • Français

On Higher Moments of Fourier Coefficients of Holomorphic Cusp Forms

Published online by Cambridge University Press:  20 November 2018

Guangshi Lü
Guangshi Lü*
Affiliation:
Department of Mathematics, Shandong University, Jinan Shandong, 250100, China email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 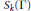${{S}_{k}}(\Gamma )$ be the space of holomorphic cusp forms of even integral weight $k$ for the full modular group. Let 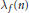${{\lambda }_{f}}(n)$ and 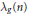${{\lambda }_{g}}(n)$ be the $n$-th normalized Fourier coefficients of two holomorphic Hecke eigencuspforms 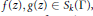$f(z),\,g(z)\,\in \,{{S}_{k}}(\Gamma )$, respectively. In this paper we are able to show the following results about higher moments of Fourier coefficients of holomorphic cusp forms.

(i)For any 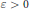$\varepsilon \,>\,0$, we have

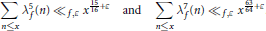$$\sum\limits_{n\le x}{\lambda _{f}^{5}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{15}{16}+\varepsilon }}\text{and}\sum\limits_{n\le x}{\lambda _{f}^{7}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{63}{64}+\varepsilon }}.$$

(ii)If 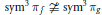$\text{sy}{{\text{m}}^{3\,}}{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{3\,}}{{\pi }_{g}}\,$, then for any 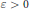$\varepsilon \,>\,0$, we have

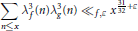$$\sum\limits_{n\le x}{\lambda _{f}^{3}(n)\lambda _{g}^{3}(n){{\ll }_{f,\varepsilon }}}{{x}^{\frac{31}{32}+\varepsilon }};$$

If 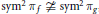$\text{sy}{{\text{m}}^{2}}\,{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{2}}\,{{\pi }_{g}}$, then for any $\varepsilon \,>\,0$, we have

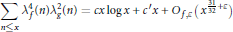$$\sum\limits_{n\le x}{\lambda _{f}^{4}(n)\lambda _{g}^{2}(n)}=cx\log x+{c}'x+{{O}_{f,\varepsilon }}({{x}^{\frac{31}{32}+\varepsilon }});$$

If 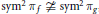$\text{sy}{{\text{m}}^{2}}\,{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{2}}\,{{\pi }_{g}}$ and 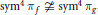$\text{sy}{{\text{m}}^{4}}{{\pi }_{f}}\,\ncong \,\text{sy}{{\text{m}}^{4}}{{\pi }_{g}}$, then for any 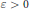$\varepsilon \,>\,0$, we have

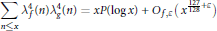$$\sum\limits_{n\le x}{\lambda _{f}^{4}(n)\lambda _{g}^{4}(n)}=xP(\log x)+{{O}_{f,\varepsilon }}({{x}^{\frac{127}{128}+\varepsilon }}),$$

where 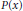$P\left( x \right)$ is a polynomial of degree 3.

Keywords

11F3011F1111F66Fourier coefficients of cusp formssymmetric power L-function
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 3 , 01 June 2011 , pp. 634 - 647
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Cogdell, J. and Michel, P., On the complex moments of symmetric power L-functions at s = 1. Int. Math. Res. Not. 2004(2004), no. 31, 1561–1617.Google Scholar
[2] Deligne, P., La conjecture de Weil. Inst. Hautes Études Sci. Publ. Math. 43(1974), 273–307.Google Scholar
[3] Fomenko, O. M., Fourier coefficients of parabolic forms and automorphic L-functions. J. Math. Sci. 95(1999), no. 3, 2295–2316.Google Scholar
[4] Friedlander, J. B. and Iwaniec, H., Summation formulae for coefficients of L-functions. Canad. J.Math. 57(2005), no. 3, 494–505.Google Scholar
[5] Gelbart, S. and Jacquet, H., A relation between automorphic representations of GL(2) and GL(3). Ann. Sci. École Norm. Sup. 11(1978), no. 4, 471–542.Google Scholar
[6] Hafner, J. L. and Ivic’, A., On sums of Fourier coefficients of cusp forms. Enseign. Math. 35(1989), no. 3–4, 375–382.Google Scholar
[7] Iwaniec, H. and Kowalski, E., Analytic number theory. American Mathematical Society Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
[8] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I. Amer. J. Math. 103(1981), no. 3, 499–558. doi:10.2307/2374103 Google Scholar
[9] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic forms. II. Amer. J. Math. 103(1981), no. 4, 777–815. doi:10.2307/2374050 Google Scholar
[10] Kim, H., Functoriality for the exterior square of GL4 and symmetric fourth of GL2. Appendix 1 by D. Ramakrishnan, Appendix 2 by Kim, H. and Sarnak, P., J. Amer. Math. Soc. 16(2003), no. 1, 139–183. doi:10.1090/S0894-0347-02-00410-1 Google Scholar
[11] Kim, H. H. and Shahidi, F., Functorial products for GL2 × GL3 and the symmetric cube for GL2. with an appendix by Bushnell, C. J. and Henniart, G., Ann. of Math. 155(2002), no. 3, 837–893. doi:10.2307/3062134 Google Scholar
[12] Kim, H. H. and Shahidi, F., Cuspidality of symmetric power with applications. Duke Math. J. 112(2002), no. 1, 177–197. doi:10.1215/S0012-9074-02-11215-0 Google Scholar
[13] Lü, G. S., Average behavior of Fourier coefficients of cusp forms. Proc. Amer. Math. Soc. 137(2009), no. 6, 1961–1969.Google Scholar
[14] Lü, G. S., The sixth and eighth moments of Fourier coefficients of cusp forms. J. Number Theory 129(2009), no. 11, 2790–2800. doi:10.1016/j.jnt.2009.01.019 Google Scholar
[15] Moreno, C. J. and Shahidi, F., The fourth moment of the Ramanujan . -function. Math. Ann. 266(1983), no. 2, 233–239. doi:10.1007/BF01458445 Google Scholar
[16] Rankin, R. A., Contributions to the theory of Ramanujan's function . (n) and similar arithemtical functions. II. The order of the Fourier coefficients of the integral modular forms. Proc. Cambridge Phil. Soc. 35(1939), 351–372. doi:10.1017/S0305004100021095 Google Scholar
[17] Rankin, R. A., Sums of cusp form coefficients. In: Automorphic forms and analytic number theory (Montreal, PQ, 1989), Univ. Montréal, Montreal, QC, 1990, pp. 115–121.Google Scholar
[18] Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory. Duke Math. J. 81(1996), no. 2, 269–322. doi:10.1215/S0012-7094-96-08115-6 Google Scholar
[19] Selberg, A., Bemerkungen über eine Dirichletsche Reihe, die mit der Theorie der Modulformen nahe verbunden ist. Arch. Math. Naturvid. 43(1940), 47–50.Google Scholar
[20] Shahidi, F., Third symmetric power L-functions for GL(2). Compositio. Math. 70(1989), no. 3, 245–273.Google Scholar
[21] Shahidi, F., On certain L-functions. Amer. J. Math. 103(1981), no. 2, 297–355. doi:10.2307/2374219 Google Scholar
[22] Shahidi, F., Fourier transforms of intertwining operators and Plancherel measures for GL(n). Amer. J. Math. 106(1984), no. 1, 67–111. doi:10.2307/2374430 Google Scholar
[23] Shahidi, F., Local coefficients as Artin factors for real groups. Duke Math. J. 52(1985), no. 4, 973–1007. doi:10.1215/S0012-7094-85-05252-4 Google Scholar
[24] Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Math. 132(1990), no. 2, 273–330. doi:10.2307/1971524 Google Scholar
[25] Wu, J., Power sums of Hecke eigenvalues and application. Acta. Arith. 137(2009), no. 4, 333–344. doi:10.4064/aa137-4-3 Google Scholar