Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T05:29:21.967Z Has data issue: false hasContentIssue false
  • English
  • Français

On Finite Nilpotent Groups

Published online by Cambridge University Press:  20 November 2018

G. Bachman
G. Bachman*
Affiliation:
Rutgers University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that if (n, ϕ(n)) = 1, where ϕ(n) denotes the Euler ϕ function, then the only group of order n is the cyclic group. This is a special case of a more general result due to Dickson (2, p. 201); namely, if

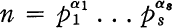
where the pi are distinct primes and each αi > 0, the necessary and sufficient conditions that the only groups of order n are abelian are (1) each αi ≤ 2 and (2) no

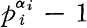
is divisible by any p1 … , ps.

We wish to establish a theorem which includes these two results. We let G(n) equal the number of groups of order n where

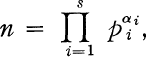
and we seek necessary and sufficient conditions on n so that

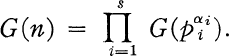
Clearly, this problem is equivalent to finding necessary and sufficient conditions on n so that all existing groups of order n be nilpotent.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 68 - 72
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Cartan, H. and Eilenberg, S., Homological algebra (Princeton, 1956).Google Scholar
2. Dickson, L.E., Trans. Amer. Math. Soc. 6 (1905), 201.Google Scholar
3. Kurosh, A.G., The theory of groups, vol. II (New York, 1956).Google Scholar
4. Zassenhaus, H., The theory of groups (New York, 1949).Google Scholar