No CrossRef data available.
Article contents
On Σ-Finite Families
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let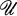 
be a family of subsets of a topological space X. We do not require 
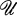to be a covering of X, nor do we assume that the members of 
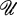are necessarily open. In this paper we shall assume that 
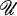is of a special sort, which we call Σ-Finite. We show that a Σ-Finite family is both locally finite and star-finite, and in particular that an open covering 
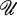of X is Σ-Finite if and only if it is star-finite. We then prove that every Σ-Finite family 
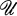is ᓂ-discrete, so that in particular, every star-finite open covering of X is (ᓂ-discrete. There seems to be some applications of this fact.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1975
References
1.
Heath, R. W., Screenability, pointwise paracompactness, and metrization of Moore spaces,
Can. J. Math. 16 (1964), 763–770.Google Scholar
You have
Access