Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T18:08:00.696Z Has data issue: false hasContentIssue false
  • English
  • Français

On Derivations of Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Stephen Berman
Stephen Berman*
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A well known result in the theory of Lie algebras, due to H. Zassenhaus, states that if 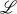is a finite dimensional Lie algebra over the field K such that the killing form of 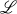is non-degenerate, then the derivations of 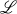are all inner, [3, p. 74]. In particular, this applies to the finite dimensional split simple Lie algebras over fields of characteristic zero. In this paper we extend this result to a class of Lie algebras which generalize the split simple Lie algebras, and which are defined by Cartan matrices (for a definition see § 1). Because of the fact that the algebras we consider are usually infinite dimensional, the method we employ in our investigation is quite different from the standard one used in the finite dimensional case, and makes no reference to any associative bilinear form on the algebras.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 174 - 180
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Berman, S., On the construction of simple lie algebras, J. Algebra 27 (1973), 158–183.Google Scholar
2. Berman, S., M∞dy, R., Wonenburger, M., Cartan matrices with null r∞ts and finite Cartan matrices, Indiana Univ. Math. J. 21 (1972), 1091–1099.Google Scholar
3. Jacobson, N., Lie algebras (Interscience, New York, 1962).Google Scholar
4. Kac, V. G., Simple irreducible graded Lie algebras of finite growth, Math. U.S.S.R.-Izv. 2 (1968), 1271–1311.Google Scholar
5. Marcuson, R., Representation and radicals of a class of infinite dimensional Lie algebras, Indiana Univ. Math. J. 23 (1974), 883–887.Google Scholar
6. M∞dy, R., A new class of Lie algebras, J. Algebra, 10 (1968), 211–230.Google Scholar
7. M∞dy, R., Euclidean Lie algebras, Can. J. Math. 21 (1969), 1432–1454.Google Scholar
8. Seligman, G. B., Modular Lie algebras (Springer-Verlag, Berlin/Heidelberg, 1967).Google Scholar