Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-27T21:41:09.444Z Has data issue: false hasContentIssue false
  • English
  • Français

On Connected Components of Shimura Varieties

Published online by Cambridge University Press:  20 November 2018

Thomas J. Haines
Thomas J. Haines*
Affiliation:
University of Toronto Department of Mathematics 100 St. George Street Toronto, ON M5S 3G3, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the cohomology of connected components of Shimura varieties 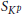${{S}_{Kp}}$ coming from the group 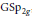$\text{GS}{{\text{p}}_{2g}}$, by an approach modeled on the stabilization of the twisted trace formula, due to Kottwitz and Shelstad. More precisely, for each character $\bar{\omega }$ on the group of connected components of 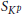${{S}_{Kp}}$ we define an operator 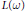$L(\omega )$ on the cohomology groups with compact supports 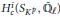$H_{c}^{i}\left( {{S}_{Kp,}}{{\overset{-}{\mathop{\mathbb{Q}}}\,}_{\ell }} \right)$, and then we prove that the virtual trace of the composition of 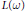$L(\omega )$ with a Hecke operator 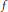$f$ away from 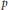$p$ and a sufficiently high power of a geometric Frobenius 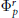$\Phi _{p}^{r}$, can be expressed as a sum of $\omega$-weighted (twisted) orbital integrals (where $\omega$-weighted means that the orbital integrals and twisted orbital integrals occuring here each have a weighting factor coming from the character $\bar{\omega }$). As the crucial step, we define and study a new invariant 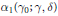${{\alpha }_{1}}\left( {{\gamma }_{0}};\gamma ,\delta \right)$ which is a refinement of the invariant 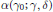$\alpha \left( {{\gamma }_{0}},\,\gamma ,\,\delta \right)$ defined by Kottwitz. This is done by using a theorem of Reimann and Zink.

Keywords

14G3511F70
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 2 , 01 April 2002 , pp. 352 - 395
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Deligne, P., Travaux de Shimura. Sém. Bourbaki Février 1971, Exposé 389, Lecture Notes in Math. 244, Springer, Heidelberg, 1971.Google Scholar
[2] Flicker, Y. and Kazhdan, D., Geometric Ramanujan Conjecture and Drinfeld Reciprocity Law. In: Number Theory, Trace Formulas, and Discrete Groups: Symposium in Honor of Atle Selberg (eds. K. Aubert, E. Bombieri, D. Goldfeld), Academic Press, 1989, 201–218.Google Scholar
[3] Fujiwara, K., Rigid Geometry, Lefschetz-Verdier trace formula and Deligne's conjecture. Invent. Math. 127 (1997), 489–533.Google Scholar
[4] Hales, T., Shalika Germs on GSp(4). Astérisque 171–172 (1989), 195–256.Google Scholar
[5] Ihara, Y., Hecke Polynomials as congruence ζ-functions in elliptic modular case. Ann. of Math. (2) 85, 1967, 267–295.Google Scholar
[6] Kottwitz, R., Stable trace formula: cuspidal tempered terms. Duke Math. J. (3) 51 (1984), 611–650.Google Scholar
[7] Kottwitz, R., Isocrystals with additional structure. Compositio Math. (2) 56 (1985), 201–220 Google Scholar
[8] Kottwitz, R., Stable trace formula: elliptic singular terms. Math. Ann. (3) 275 (1986), 365–399.Google Scholar
[9] Kottwitz, R., Shimura varieties and λ-adic representations. In: Automorphic Forms, Shimura Varieties and L-functions, Part I, Perspectives in Mathematics Vol. 10, Academic Press, San Diego, CA, 1990, 161–209.Google Scholar
[10] Kottwitz, R., On the λ-adic representations associated to some simple Shimura varieties. Invent. Math. 108 (1992), 653–665.Google Scholar
[11] Kottwitz, R., Points on some Shimura varieties over finite fields. J. Amer. Math. Soc. 5 (1992), 373–444.Google Scholar
[12] Kottwitz, R., Isocrystals with additional structure II. Compositio Math. (3) 109 (1997), 255–339.Google Scholar
[13] Kottwitz, R. and Shelstad, D., Foundations of twisted endoscopy. Astérisque 255, 1999.Google Scholar
[14] Langlands, R. P., Some contemporary problems with origins in the Jugendtraum. In: Mathematical Developments Arising from Hilbert Problems, Proc. Symp. Pure Math. 28, Amer. Math. Soc., Providence, RI, 1976, 401–418.Google Scholar
[15] Langlands, R. P., Shimura varieties and the Selberg trace formula. Canad. J. Math. (5) 29 (1977), 1292–1299.Google Scholar
[16] Langlands, R. P., On the zeta-functions of some simple Shimura varieties. Canad. J. Math. (6) 31 (1979), 1121–1216.Google Scholar
[17] Langlands, R. P. and Ramakrishnan, D. (eds.), The Zeta Function of Picard Modular Surfaces. Univ. Montréal, Montréal, QC, 1992.Google Scholar
[18] Langlands, R. P. and Rapoport, M., Shimuravarietäten und Gerben. J. Reine Angew. Math. 378 (1987), 113–220.Google Scholar
[19] Laumon, G., Sur la cohomologie à supports compacts des variétés de Shimura pour GSp(4)Q. Compositio Math. (3) 105 (1997), 267–359.Google Scholar
[20] Milne, J. S., Étale Cohomology. Princeton Math. Series 33, Princeton Univ. Press, 1980.Google Scholar
[21] Milne, J. S., The points on a Shimura variety modulo a prime of good reduction. In: The zeta functions of Picard modular surfaces, Univ. Montréal, Montréal, PQ, 1992, 151–253.Google Scholar
[22] Mumford, D., Abelian varieties. Tata Institute of Fundamental Research Studies in Mathematics 5. Published for the Tata Institute of Fundamental Research, Bombay; Oxford University Press, London 1970.Google Scholar
[23] Mumford, D., Geometric invariant theory. Springer, Heidelberg, 1965.Google Scholar
[24] Pfau, M., The reduction of connected Shimura varieties at primes of good reduction. Dissertation, University of Michigan, 1993.Google Scholar
[25] Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory. Pure Appl. Math. 139, Academic Press, Inc., 1994.Google Scholar
[26] Reimann, H., The semi-simple zeta function of quaternionic Shimura varieties. Lecture Notes in Math. 1657, Springer-Verlag, 1997.Google Scholar
[27] Reimann, H. and Zink, Th., Der Dieudonńemodul einer polarisierten abelschen Mannigfaltigkeit vom CM-Typ. Ann. of Math. (2) 128 (1988), 461–482.Google Scholar
[28] Serre, J. P., Corps locaux. Hermann, Paris, 1962.Google Scholar
[29] Shimura, G., Correspondances modulaires et les fonctions ζ de courbes algébriques. J. Math. Soc. Japan 10 (1958), 1–28.Google Scholar
[30] Shimura, G., On the zeta-functions of the algebraic curves uniformized by certain automorphic functions. J. Math. Soc. Japan 13 (1961), 275–331.Google Scholar
[31] Shimura, G., Construction of class fields and zeta functions of algebraic curves. Ann. of Math. 85 (1967), 58–159.Google Scholar
[32] Tate, J., Classes d’isogénie des variétés abéliennes sur un corps fini (d’après T. Honda). Sém. Bourbaki Nov. 1968, Exposé 352.Google Scholar
[33] Waldspurger, J.-L., Quelques résultats de finitude concernant les distributions invariantes sur les algébres de Lie p-adiques. Preprint.Google Scholar
[34] Waldspurger, J.-L., Homogéńeité de certaines distributions sur les groupes p-adiques. Preprint.Google Scholar
[35] Weissauer, R., A special case of the fundamental lemma. Preprints, Parts I, II, III, IV.Google Scholar