No CrossRef data available.
Article contents
On Conics Over a Finite Field
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let F denote a Galois field of order q and odd characteristic p, and F* = F\{0}. Let Sn denote an n-dimensional affine space with base field F. E. Cohen [1] had proved that if n ≧ 4, there is no hyperplane of Sn contained in the complement of the quadric Qn of Sn defined by
1.1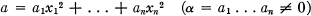
and in S3, there are q + 1 or 0 planes contained in the complement of Q3 according as — aα is not or is a square of F.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974
References
1.
Cohen, E., Linear and quadratic equations in a Galois field with applications to geometry, Duke Math. J.
32 (1965), 633–641.Google Scholar
2.
Dickson, L. E., Linear group, with an exposition of the Galois field theory, (Lipezig, 1901: reprinted by Dover, 1958).Google Scholar


