Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T07:29:08.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On Certain Onto Maps

Published online by Cambridge University Press:  20 November 2018

Isaac Namioka
Isaac Namioka*
Affiliation:
Cornell University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δn (n > 0) denote the subset of the Euclidean (n + 1)-dimensional space defined by

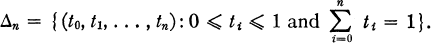
A subset σ of Δn is called a face if there exists a sequence 0 ≤ i1 ≤ i2 ≤ … < im ≤ n such that

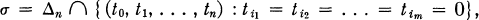
and the dimension of σ is defined to be (n — m). Let 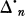denote the union of all faces of Δn of dimensions less than n. A topological space Y is called solid if any continuous map on a closed subspace A of a normal space X into Y can be extended to a map on X into Y. By Tietz's extension theorem, each face of Δn is solid. The present paper is concerned with a generalization of the following theorem which seems well known.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 461 - 466
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Day, M. M., Normed linear spaces, (Berlin, 1958).Google Scholar
2. Eilenberg, S. and Steenrod, N., Foundations of algebraic topology, (Princeton 1952).Google Scholar
3. Fan, K., Fixed-point and minimax theorems in locally convex topological linear spaces, Proc. Nat. Acad. Sci. U.S.A., 38 (1952), 121–126.Google Scholar
4. Hu, S-T., Homotopy theory, (New York, 1959).Google Scholar
5. Kelley, J. L., General topology, (New York, 1955).Google Scholar
6. Kiefer, J., An extremum result, Can. J. Math., 14 (1962), 000–000.Google Scholar