Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T02:48:25.542Z Has data issue: false hasContentIssue false
  • English
  • Français

On Cardinal Invariants and Generators for von Neumann Algebras

Published online by Cambridge University Press:  20 November 2018

David Sherman
David Sherman*
Affiliation:
Department of Mathematics, University of Virginia, P.O. Box 400137, Charlottesville, VA 22904, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We demonstrate how most common cardinal invariants associated with a von Neumann algebra 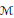$\mathcal{M}$ can be computed from the decomposability number, 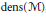$\text{dens}\left( \mathcal{M} \right)$, and the minimal cardinality of a generating set, 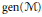$\text{gen}\left( \mathcal{M} \right)$. Applications include the equivalence of the well-known generator problem, “Is every separably-acting von Neumann algebra singly-generated?”, with the formally stronger questions, “Is every countably-generated von Neumann algebra singly-generated?” and “Is the gen invariant monotone?” Modulo the generator problem, we determine the range of the invariant 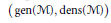$\left( \text{gen}\left( \mathcal{M} \right),\,\text{dens}\left( \mathcal{M} \right) \right)$ , which is mostly governed by the inequality 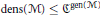$\text{dens}\left( \mathcal{M} \right)\,\le {{\mathfrak{C}}^{\text{gen}\left( \mathcal{M} \right)}}$.

Keywords

46L10von Neumann algebracardinal invariantgenerator problemdecomposability numberrepresentation density
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 2 , 16 April 2012 , pp. 455 - 480
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Akemann, C. A. and Anderson, J. Lyapunov theorems for operator algebras. Mem. Amer. Math. Soc. 94(1991).Google Scholar
[2] Behncke, H., Generators of finite W*-algebras. Tôhoku Math. J. 24(1972), 401–408. http://dx.doi.org/10.2748/tmj/1178241478 Google Scholar
[3] Behncke, H., Topics in C*-and von Neumann algebras. In: Lectures on Operator Algebras (Tulane Univ. Ring and Operator Theory Year, 1970–1971, Vol. II), Lecture Notes in Math. 247, Springer, Berlin, 1972, 1–54.Google Scholar
[4] Blackadar, B., Operator Algebras: Theory of C*-Algebras and von Neumann Algebras. In: Encyclopaedia of Mathematical Sciences 122, Operator Algebras and Non-commutative Geometry III, Springer-Verlag, Berlin, 2006.Google Scholar
[5] Comfort, W. W., A survey of cardinal invariants. General Topology and Appl. 1(1971), 163–199. http://dx.doi.org/10.1016/0016-660X(71)90122-X Google Scholar
[6] Comfort, W. W. and Itzkowitz, G. L., Density character in topological groups. Math. Ann. 226(1977), 223–227. http://dx.doi.org/10.1007/BF01362424 Google Scholar
[7] Dixmier, J., Les algèbres d’opérateurs dans l’espace hilbertien (Algèbres de von Neumann). Second edition, Gauthier-Villars, Paris, 1969.Google Scholar
[8] Dykema, K., Sinclair, A. Smith, R. and S.White, Generators of II1 factors. Oper. Matrices 2(2008), 555–582.Google Scholar
[9] Elliott, G. A., On approximately finite-dimensional von Neumann algebras. Math. Scand. 39(1976), 91–101.Google Scholar
[10] Farah, I. and Katsura, T. Nonseparable UHF algebras I: Dixmier's problem. Adv. Math., to appear. http://dx.doi.org/10.1016/j.aim.2010.04.006 Google Scholar
[11] Feldman, J., Nonseparability of certain finite factors. Proc. Amer. Math. Soc. 7(1956), 23–26. http://dx.doi.org/10.1090/S0002-9939-1956-0079742-X Google Scholar
[12] Ge, L. and Popa, S. On some decomposition properties for factors of type II1. Duke Math. J. 94(1998), 79–101. http://dx.doi.org/10.1215/S0012-7094-98-09405-4 Google Scholar
[13] Ge, L. and Shen, J. On the generator problem of von Neumann algebras. In: Third International Congress of Chinese Mathematicians, Part 1, 2, AMS/IP Stud. Adv. Math. 42, pt. 1, 2, Amer. Math. Soc., Providence, RI, 2008, 357–375.Google Scholar
[14] Haagerup, U., The standard form of von Neumann algebras. Math. Scand. 37 (1975), 271–283.Google Scholar
[15] Hewitt, E., A remark on density characters. Bull. Amer. Math. Soc. 52(1946), 641–643. http://dx.doi.org/10.1090/S0002-9904-1946-08613-9 Google Scholar
[16] Hu, Z., Maximally decomposable von Neumann algebras on locally compact groups and duality. Houston J. Math. 31(2005), 857–881.Google Scholar
[17] Hu, Z. and Neufang, M. Decomposability of von Neumann algebras and the Mazur property of higher level. Canad. J. Math. 58(2006), 768–795. http://dx.doi.org/10.4153/CJM-2006-031-7 Google Scholar
[18] Jech, T., Set Theory. Third edition, Springer-Verlag, Berlin, 2003.Google Scholar
[19] Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras II. Graduate Studies in Mathematics 16, Amer. Math. Soc., Providence, 1997.Google Scholar
[20] Kaplansky, I., Quelques résultats sur les anneaux d’opérateurs. C. R. Acad. Sci. Paris 231(1950), 485–486.Google Scholar
[21] Kehlet, E. T., Disintegration theory on a constant field of nonseparable Hilbert spaces. Math. Scand. 43(1978), 353–362.Google Scholar
[22] Kruse, A. H., Badly incomplete normed linear spaces. Math. Z. 83(1964), 314–320. http://dx.doi.org/10.1007/BF01111164 Google Scholar
[23] Marczewski, E., Séparabilité et multiplication cartésienne des espaces topologiques. Fund. Math. 34(1947), 127–143.Google Scholar
[24] Murray, F. J. and von Neumann, J., On rings of operators IV. Ann. of Math. (2) 44(1943), 716–808. http://dx.doi.org/10.2307/1969107 Google Scholar
[25] Neufang, M., On Mazur's property and property (X). J. Operator Theory 60(2008), 301–316.Google Scholar
[26] von Neumann, J., Zur Algebra der Funktionaloperatoren und Theorie der normalen Operatoren. Math. Ann. 102(1929), 370–427.Google Scholar
[27] Pearcy, C., W*-algebras with a single generator. Proc. Amer. Math. Soc. 13(1962), 831–832.Google Scholar
[28] Pearcy, C., On certain von Neumann algebras which are generated by partial isometries. Proc. Amer. Math. Soc. 15(1964), 393–395. http://dx.doi.org/10.1090/S0002-9939-1964-0161172-8 Google Scholar
[29] Pedersen, G. K., Applications of weak semicontinuity in C*-algebra theory. Duke Math. J. 39(1972), 431–450. http://dx.doi.org/10.1215/S0012-7094-72-03950-6 Google Scholar
[30] Pedersen, G. K., C*-Algebras and Their Automorphism Groups. London Mathematical Society Monographs 14, Academic Press, London–New York, 1979.Google Scholar
[31] Pondiczery, E. S., Power problems in abstract spaces. Duke Math. J. 11(1944), 835–837. http://dx.doi.org/10.1215/S0012-7094-44-01171-3 Google Scholar
[32] Popa, S., On a problem of Kadison on R. V. maximal abelian C-subalgebras in factors. Invent. Math. 65(1981/82), 269–281. http://dx.doi.org/10.1007/BF01389015 Google Scholar
[33] Powers, R. T., Representations of uniformly hyperfinite algebras and their associated von Neumann rings. Ann. of Math. (2) 86(1967), 138–171. http://dx.doi.org/10.2307/1970364 Google Scholar
[34] Raynaud, Y., On ultrapowers of non commutative Lp spaces. J. Operator Theory 48(2002), 41–68.Google Scholar
[35] Rickart, C. E., General Theory of Banach Algebras. D. van Nostrand, New York, 1960.Google Scholar
[36] Saitô, T., Generations of von Neumann algebras. In: Lectures on Operator Algebras (Tulane Univ. Ring and Operator Theory Year, 1970–1971, Vol. II), Lecture Notes in Math. 247, Springer, Berlin, 1972, 435–531.Google Scholar
[37] Sakai, S., C*-Algebras and W*-Algebras. Springer–Verlag, New York, 1971.Google Scholar
[38] Shen, J., Type II1 factors with a single generator. J. Operator Theory 62(2009), 421–438.Google Scholar
[39] Sherman, D., On the dimension theory of von Neumann algebras. Math. Scand. 101(2007), 123–147.Google Scholar
[40] Smith, R. R. and Sinclair, A. M., Hochschild Cohomology of Von Neumann Algebras. London Mathematical Society Lecture Note Series 203, Cambridge University Press, Cambridge, 1995.Google Scholar
[41] Smith, R. R. and Sinclair, A. M., Finite von Neumann Algebras and Masas. London Mathematical Society Lecture Note Series 351, Cambridge University Press, Cambridge, 2008.Google Scholar
[42] Suzuki, N. and Saitô, T., On the operators which generate continuous von Neumann algebras. Tôhoku Math. J. 15(1963), 277–280. http://dx.doi.org/10.2748/tmj/1178243811 Google Scholar
[43] Voiculescu, D., Circular and semicircular systems and free product factors. In: Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory (Paris, 1989), Progr. Math. 92, Birkhäuser, Boston, 1990, 45–60.Google Scholar
[44] Weaver, N., Mathematical Quantization. Studies in Advanced Mathematics, Chapman & Hall/CRC, Boca Raton, 2001.Google Scholar
[45] Willig, P., On hyperfinite W*-algebras. Proc. Amer. Math. Soc. 40(1973), 120–122.Google Scholar
[46] Willig, P., Generators and direct integral decompositions of W*-algebras. Tôhoku Math. J. 26(1974), 35–37. http://dx.doi.org/10.2748/tmj/1178241231 Google Scholar
[47] Wogen, W., On generators for von Neumann algebras. Bull. Amer. Math. Soc. 75(1969), 95–99. http://dx.doi.org/10.1090/S0002-9904-1969-12157-9 Google Scholar
[48] Yamagami, S., Notes on operator categories. J. Math. Soc. Japan 59(2007), 541–555. http://dx.doi.org/10.2969/jmsj/05920541Google Scholar