Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T06:07:56.240Z Has data issue: false hasContentIssue false
  • English
  • Français

On Best Proximity Points in Metric and Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Rafa Espínola  and
Aurora Fernández-León
Rafa Espínola
Affiliation:
Departamento de Análisis Matemático, Facultad de Matemáticas, Universidad de Sevilla, 41080-Sevilla, Spain email: [email protected]@us.es
Aurora Fernández-León
Affiliation:
Departamento de Análisis Matemático, Facultad de Matemáticas, Universidad de Sevilla, 41080-Sevilla, Spain email: [email protected]@us.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the existence and uniqueness of best proximity points of cyclic contractions as well as the convergence of iterates to such proximity points. We take two different approaches, each one leading to different results that complete, if not improve, other similar results in the theory. Results in this paper stand for Banach spaces, geodesic metric spaces and metric spaces. 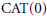We also include an appendix on $\text{CAT(0)}$ spaces where we study the particular behavior of these spaces regarding the problems we are concerned with.

Keywords

54H2547H09
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 3 , 01 June 2011 , pp. 533 - 550
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Ayerbe Toledano, J. M., Domınguez Benavides, T., and López Acedo, G., Measures of noncompactness in metric fixed point theory. Operator Theory: Advances and Applications, 99, Birkhäuser Verlag, Basel, 1997.Google Scholar
[2] Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften, 319, Springer-Verlag, Berlin, 1999.Google Scholar
[3] Eldred, A. A. and Veeramani, P., Existence and convergence of best proximity points. J. Math. Anal. Appl. 323(2006), no. 2, 1001–1006. doi:10.1016/j.jmaa.2005.10.081 Google Scholar
[4] Eldred, A. A., Kirk, W. A., and Veeramani, P., Proximal normal structure and relatively nonexpansive mappings. Studia Math. 171(2005), no. 3, 283–293. doi:10.4064/sm171-3-5 Google Scholar
[5] Espınola, R., A new approach to relatively nonexpansive mappings. Proc. Amer. Math. Soc. 136(2008), no. 6, 1987–1995. doi:10.1090/S0002-9939-08-09323-4 Google Scholar
[6] Espınola, R. and Ferńandez-León, A., CAT(k)-spaces, weak convergence and fixed points. J. Math. Anal. Appl. 353(2009), no. 1, 410–427. doi:10.1016/j.jmaa.2008.12.015 Google Scholar
[7] Ferńandez-León, A., Existence and uniqueness of best proximity points in geodesic metric spaces. Nonlinear Anal. 73(2010), no. 4, 915–921. doi:10.1016/j.na.2010.04.005 Google Scholar
[8] Goebel, K. and Kirk, W. A., Topics in metric fixed point theory. Cambridge Studies in Advanced Mathematics, 28, Cambridge Univ. Press, Cambridge, 1990.Google Scholar
[9] Goebel, K. and Reich, S., Uniform convexity, hyperbolic geometry, and nonexpansive mappings. Monographs and Textbooks in Pure and Applied Mathematics, 83, Marcel Dekker, Inc., New York, 1984.Google Scholar
[10] Jachymski, J., Matkowski, J., and T. Świątkowski, Nonlinear contractions on semimetric spaces. J. Appl. Anal. 1(1995), no. 2, 125–134. doi:10.1515/JAA.1995.125 Google Scholar
[11] Kirk, W. A. and Panyanak, B., A concept of convergence in geodesic spaces. Nonlinear Anal. 68(2008), no. 12, 3689–3696. doi:10.1016/j.na.2007.04.011 Google Scholar
[12] Kirk, W. A., Reich, S., and Veeramani, P., Proximal retracts and best proximity pairs theorems. Numer. Funct. Anal. Optim. 24(2003), no. 7–8, 851–862. doi:10.1081/NFA-120026380 Google Scholar
[13] Kirk, W. A. and Sims, B. eds., Handbook of metric fixed point theory. Kluwer Academic Publishers, Dordrecht, 2001.Google Scholar
[14] Leustean, L., A quadratic rate of asymptotic regularity for CAT(0)-spaces. J. Math. Anal. Appl. 325(2007), no. 1, 386–399. doi:10.1016/j.jmaa.2006.01.081 Google Scholar
[15] Lin, B.-L. P.-K., Lin and Troyanski, S. L., Some geometric and topological properties of the unit sphere in a Banach space. Math. Ann. 274(1986), no. 4, 613–616. doi:10.1007/BF01458596 Google Scholar
[16] Papadopoulus, A., Metric spaces, convexity and nonpositive curvature. IRMA Lectures in Mathematics and Theoretical Physics, 6, European Mathematical Society, Zürich, 2005.Google Scholar
[17] Piątek, B., On cyclic Meir-Keeler contractions in metric spaces. Nonlinear Anal. 74(2011), no. 1, 35–40.Google Scholar
[18] Suzuki, T., Kikkawa, M., and Vetro, C., The existence of best proximity points in metric spaces with the UC property. Nonlinear Anal. 71(2009), no. 7–8, 2918–2926. doi:10.1016/j.na.2009.01.173 Google Scholar