Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T03:32:24.627Z Has data issue: false hasContentIssue false
  • English
  • Français

On Asymptotic Centers and Fixed Points of Nonexpansive Mappings

Published online by Cambridge University Press:  20 November 2018

Teck-Cheong Lim
Teck-Cheong Lim*
Affiliation:
George Mason University, Fairfax, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

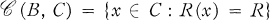Let X be a Banach space and B a bounded subset of X. For each x ∈ X, define R(x) = sup{‖x – y‖ : y ∈ B}. If C is a nonempty subset of X, we call the number R = inƒ{R(x) : x ∈ C} the Chebyshev radius of B in C and the set the Chebyshev center of B in C. It is well known that if C is weakly compact and convex, then 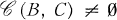and if, in addition, X is uniformly convex, then the Chebyshev center is unique; see e.g., [9].

Let {Bα : α ∈ ∧} be a decreasing net of bounded subsets of X. For each x ∈ X and each α ∈ ∧, define

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 421 - 430
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Anderson, C. L., Hyams, W. H. and McKnight, C. K., Center points of nets, Can. J. Mat. 27 (1975), 418–422.Google Scholar
2. Belluce, L. P. and Kirk, W. A., Fixed-point theorems for families of contraction mappings, Pacific J. Math. 18, No. 2, (1966), 213–217.Google Scholar
3. Bynum, W. L., A Class of spaces lacking normal structure, Compositio Math., 25, Fasc. 3 (1972), 233–236.Google Scholar
4. Clarkson, J. A., Uniformly convex spaces, Trans. Amer. Math. Soc. 40 (1936), 396–414.Google Scholar
5. Caristi, J., Fixed point theorems for mappings satisfying inwardness conditions, Trans. Amer. Math. Soc. 215 (1976), 241–251.Google Scholar
6. Downing, D. and Kirk, W. A., Fixed point theorems for set-valued mappings in metric and Banach spaces, Math. Japonic. 22 (1977), 99–112.Google Scholar
7. Edelstein, M., The construction of an asymptotic center with a fixed-point property, Bull. Amer. Math. Soc. 78 (1972), 206–208.Google Scholar
8. Edelstein, M., Fixed point theorems in uniformly convex Banach spaces, Proc. Amer. Math. Soc. 44 (1974), 369–374.Google Scholar
9. Garkavi, A. L., On the Chebyshev center of a set in a normed space, Investigations of contemporary problems in the constructive theory of functions, Moscow (1961), 328–331.Google Scholar
10. Garkavi, A. L., The best possible net and the best possible cross-section of a set in a normed space, Izv. Akad. Nauk SSSR, Ser. Math. 26, (1962), 87-106; Amer. Math. Soc. Transi., Ser. 2. 39 (1964), 111–132.Google Scholar
11. Goebel, K., On a fixed point theorem for multi-valued nonexpansive mappings, Annales Univ. Maria Curie-Sklowdska.Google Scholar
12. Gurarii, V. I., On the differential properties of the modulus of convexity in a Banach space, Mat. Issled. 2 (1967), 141–148.Google Scholar
13. Holmes, R. D. and Lau, A. T., Non-expansive actions of topological semigroups and fixed points, J. London Math. Soc. (2). 5 (1972), 330–336.Google Scholar
14. Kirk, W. A., Nonexpansive mappings and the weak closure of sequences of iterates, Duke Math. Jour. 36 (1969), 639–645.Google Scholar
15. Klee, V., Circumspheres and inner products, Math. Scand. 8 (1960), 363–370.Google Scholar
16. Lim, T. C., Characterizations of normal structure, Proc. Amer. Math. Soc. 43 (1974), 313–319.Google Scholar
17. Lim, T. C., Remarks on some fixed point theorems, Proc. Amer. Math. Soc. 60 (1976), 179–182.Google Scholar
18. Lim, T. C., The asymptotic center and fixed point theorems for nonexpansive mappings, Ph.D. Thesis, Dalhousie University (1974).Google Scholar
19. Lim, T. C., A fixed point theorem for multivalued nonexpansive mappings in a uniformly convex Banach space, Bull. Amer. Math. Soc. 80 (1974), 1123–1126.Google Scholar
20. Martin, R. H., Differential equations on closed subsets of a Banach space, Trans. Amer. Math. Soc. 179 (1973), 399–414.Google Scholar