Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-30T03:35:22.071Z Has data issue: false hasContentIssue false
  • English
  • Français

On Algebraic Surfaces Termwise Invariant Under Cyclic Collineations

Published online by Cambridge University Press:  20 November 2018

J. C. Morelock  and
N. C. Perry
J. C. Morelock
Affiliation:
Alabama Polytechnic Institute
N. C. Perry
Affiliation:
Alabama Polytechnic Institute
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In algebraic geometry it is of interest to examine polynomial surfaces F which transform into themselves under the collineation T defined by:

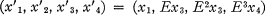
where Ep = 1, and p is a prime (2). One of the most obvious ways to ensure invariance of a surface is for each term X1ax2bX3cX4d of F to go into itself. We present initially, therefore, a theorem which will be useful in the study of such termwise invariance for polynomials of composite degree.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 7 , 1955 , pp. 204 - 207
Copyright
Copyright © Canadian Mathematical Society 1955

References

1. Dessart, J., Sur les surfaces représentant l'involution engendrée par un homographie de periode cinq du plan, Mem. Soc. royale des sciences de Liège (3), 17 (1931), 1–23.Google Scholar
2. Hutcherson, W. R., A cyclic involution of order seven, Bull. Amer. Math. Soc, 40 (1934), 143–151.Google Scholar