Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gilmour, Christopher R.A.
1983.
REAL COMPACTIFICATIONS THROUGH ZERO-SET SPACES.
Quaestiones Mathematicae,
Vol. 6,
Issue. 1-3,
p.
73.


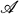 determines a Hausdorff compactification
determines a Hausdorff compactification 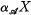 .
.
