Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T05:55:09.020Z Has data issue: false hasContentIssue false
  • English
  • Français

On Absolute Summability by Riesz and Generalized Cesàro Means. I

Published online by Cambridge University Press:  20 November 2018

H.-H. Körle
H.-H. Körle*
Affiliation:
Universitât Marburg Marburg, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. The Cesàro methods for ordinary [9, p. 17; 6, p. 96] and for absolute [9, p. 25] summation of infinite series can be generalized by the Riesz methods [7, p. 21; 12; 9, p. 52; 6, p. 86; 5, p. 2] and by “the generalized Cesàro methods“ introduced by Burkill [4] and Borwein and Russell [3]. (Also cf. [2]; for another generalization, see [8].) These generalizations raise the question as to their equivalence.

We shall consider series

(1)

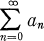
with complex terms an. Throughout, we will assume that

(2)

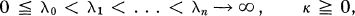
and we call (1) Riesz summable to a sum s relative to the type λ = (λn) and to the order κ, or summable (R, λ, κ) to s briefly, if the Riesz means

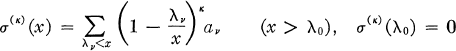
(of the partial sums of (1)) tend to s as x → ∞.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 202 - 208
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Borwein, D., On a generalised Cesàro summability method of integral order, Töhoku Math. J. 18 (1966), 71–73.Google Scholar
2. Borwein, D., On a method of summability equivalent to the Cesàro method, J. London Math. Soc. 42 (1967), 339–343.Google Scholar
3. Borwein, D. and Russell, D. C., On Riesz and generalised Cesàro summability of arbitrary positive order, Math. Z. 99 (1967), 171–177.Google Scholar
4. Burkill, H., On Riesz and Riemann summability, Proc. Cambridge Philos. Soc. 57 (1961), 55–60.Google Scholar
5. Chandrasekharan, K. and Minakshisundaram, S., Typical means (Oxford Univ. Press, London, 1952).Google Scholar
6. Hardy, G. H., Divergent series (Oxford Univ. Press, London, 1956/1963).Google Scholar
7. Hardy, G. H. and Riesz, M., The general theory of Dirichlet's series, Cambridge Tract no. 18 (University Press, Cambridge, 1915/1952).Google Scholar
8. Jurkat, W., Uber Rieszsche Mittel und verwandte Klassen von Matrixtransformationen, Math. Z. 57 (1953), 353–394.Google Scholar
9. Kogbetliantz, E., Sommation des séries et intégrales divergentes par les moyennes arithmétiques et typiques, Mémorial Sci. Math. 51 (Gauthier-Villars, Paris, 1931).Google Scholar
10. Körle, H.-H., On the equivalence of Riesz and generalized Cesàro ﹛absolute) summability. II, Notices Amer. Math. Soc. 15 (1968), 923.Google Scholar
11. Meir, A., An inclusion theorem for generalized Cesàro and Riesz means, Can. J. Math. 20 (1968), 735–738.Google Scholar
12. Obrechkoff, N., Uber die absolute Summierung der Dirichletschen Reihen, Math. Z. 30 (1929), 375–386.Google Scholar
13. Russell, D. C., On generalized Cesàro means of integral order, Töhoku Math. J. 17 (1965), 410-442; Corrigenda, ibid. 18 (1966), 454–455.Google Scholar