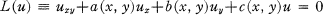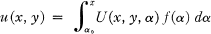Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1969.
Function Theoretic Methods in Partial Differential Equations.
Vol. 54,
Issue. ,
p.
297.