Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T05:18:58.160Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Hermite and Joubert

Published online by Cambridge University Press:  20 November 2018

Zinovy Reichstein
Zinovy Reichstein*
Affiliation:
Department of Mathematics, Oregon State University, Corvallis, OR 97331-4605, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A classical theorem of Hermite and Joubert asserts that any field extension of degree 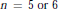$n\,=\,5\,\text{or}\,\text{6}$ is generated by an element whose minimal polynomial is of the form 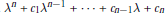${{\lambda }^{n}}\,+\,{{c}_{1}}{{\lambda }^{n-1}}\,+\,\cdot \cdot \cdot +\,{{c}_{n-1}}\lambda \,+\,{{c}_{n}}$ with ${{c}_{1\,}}\,=\,\,{{c}_{3}}\,=\,0$. We show that this theorem fails for 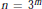$n\,=\,{{3}^{m}}$ or ${{3}^{m}}+{{3}^{l}}$ (and more generally, for 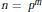$n={{p}^{m}}$ or 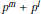${{p}^{m}}+{{p}^{l}}$, if 3 is replaced by another prime $p$), where 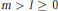$m\,>\,1\,\ge \,0$. We also prove a similar result for division algebras and use it to study the structure of the universal division algebra 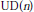$\text{UD}\left( n \right)$.

We also prove a similar result for division algebras and use it to study the structure of the universal division algebra 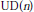$\text{UD}\left( n \right)$.

Keywords

12E0516K20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 1 , 01 February 1999 , pp. 69 - 95
Copyright
Copyright © Canadian Mathematical Society 1999

References

[A] Amitsur, S. A., On the characteristic polynomial of a sum of matrices. Linear and Multilinear Algebra 8 (1980), 177–182.Google Scholar
[BR] Buhler, J. and Reichstein, Z., On the essential dimension of a finite group. Compositio Math. 106 (1997), 159–179.Google Scholar
[C1] Coray, D., Algebraic points on cubic hypersurfaces. Acta Arith. 30 (1976), 267–296.Google Scholar
[C2] Coray, D., Cubic hypersurfaces and a result of Hermite. Duke J. Math. 54 (1987), 657–670.Google Scholar
[D] Davenport, H., Cubic forms in sixteen variables. Proc. Royal Soc. London Ser. A 272 (1963), 285–303.Google Scholar
[F] Formanek, E., Some remarks about the reduced trace. Israel Math. Conf. Proc. 1 (1989), 337–343.Google Scholar
[HB] Heath-Brown, D. R., Cubic forms in ten variables. Proc. London Math. Soc. (3) 47 (1983), no. 2, 227–257.Google Scholar
[He] Hermite, C., Sur l’invariant du dix-huitième ordre des formes du cinquième degré. J. Crelle 59 (1861), 304– 305.Google Scholar
[J] Joubert, P., Sur l’equation du sixième degré. C. R. Acad. Sci. Paris 64 (1867), 1025–1029.Google Scholar
[K] Kuyk, W., On a theorem of E. Noether. Nederl. Acad. Wetensch. Proc. Ser. A 67 (1964), 32–39.Google Scholar
[L] Lang, S., Algebra. First edition, Addison-Wesley, 1965.Google Scholar
[M] Manin, Yu. I., Cubic Forms. North Holland, Amsterdam, 1974.Google Scholar
[MD] Mac Donald, I. G., Symmetric Functions and Hall Polynomials. Clarendon Press, Oxford, 1979.Google Scholar
[Pf] Pfister, A., Quadratic Forms with Applications to Geometry and Topology. Cambridge University Press, 1995.Google Scholar
[RV] Reichstein, Z. and Vonessen, N., An embedding property of universal division algebras. J. Algebra 177 (1995), 451–462.Google Scholar
[Ro1] Rowen, L. H., Polynomial Identities in Ring Theory. Academic Press, 1980.Google Scholar
[Ro2] Rowen, L. H., Brauer factor sets and simple algebras. Trans. Amer. Math. Soc. (2) 282 (1984), 767–772.Google Scholar
[Ro3] Rowen, L. H., Ring Theory II. Academic Press, 1988.Google Scholar
[RS] Rowen, L. H. and Saltman, D. J., Prime to p extensions of division algebras. Israel J. Math. 78 (1992), 197–207.Google Scholar
[S] Saltman, D. J., Generic Galois extensions and problems in field theory. Advances in Math. 43 (1982), 250–283.Google Scholar