Published online by Cambridge University Press: 14 December 2020
In [5], Chen and Yui conjectured that Gross–Zagier type formulas may also exist for Thompson series. In this work, we verify Chen and Yui’s conjecture for the cases for Thompson series 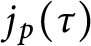 $j_{p}(\tau )$
for
$j_{p}(\tau )$
for
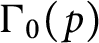 $\Gamma _{0}(p)$
for p prime, and equivalently establish formulas for the prime decomposition of the resultants of two ring class polynomials associated to
$\Gamma _{0}(p)$
for p prime, and equivalently establish formulas for the prime decomposition of the resultants of two ring class polynomials associated to
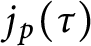 $j_{p}(\tau )$
and imaginary quadratic fields and the prime decomposition of the discriminant of a ring class polynomial associated to
$j_{p}(\tau )$
and imaginary quadratic fields and the prime decomposition of the discriminant of a ring class polynomial associated to
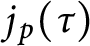 $j_{p}(\tau )$
and an imaginary quadratic field. Our method for tackling Chen and Yui’s conjecture on resultants can be used to give a different proof to a recent result of Yang and Yin. In addition, as an implication, we verify a conjecture recently raised by Yang, Yin, and Yu.
$j_{p}(\tau )$
and an imaginary quadratic field. Our method for tackling Chen and Yui’s conjecture on resultants can be used to give a different proof to a recent result of Yang and Yin. In addition, as an implication, we verify a conjecture recently raised by Yang, Yin, and Yu.
Dongxi Ye is supported by the Natural Science Foundation of China (grant No.11901586), the Natural Science Foundation of Guangdong Province (grant No.2019A1515011323), and the Sun Yat-sen University Research Grant for Youth Scholars (grant no.19lgpy244).
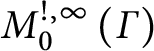 . Results Math. 74(2019), no. 2.CrossRefGoogle Scholar
. Results Math. 74(2019), no. 2.CrossRefGoogle Scholar