Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T12:01:06.656Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Class of Landsberg Metrics in Finsler Geometry

Published online by Cambridge University Press:  20 November 2018

Zhongmin Shen
Zhongmin Shen*
Affiliation:
Department of Mathematical Sciences, Indiana University Purdue University Indianapolis (IUPUI), 402 N. Blackford Street, Indianapolis, IN 46202-3216, USA and Center of Mathematical Sciences, Zhejiang University, Hangzhou, Zhejiang Province 310027, P.R. China email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

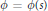In this paper, we study a long existing open problem on Landsberg metrics in Finsler geometry. We consider Finsler metrics defined by a Riemannian metric and a 1-form on a manifold. We show that a regular Finsler metric in this form is Landsbergian if and only if it is Berwaldian. We further show that there is a two-parameter family of functions, $\phi \,=\,\phi \left( s \right)$ , for which there are a Riemannian metric 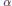$\alpha $ and a 1-form 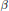$\beta $ on a manifold 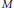$M$ such that the scalar function 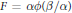$F\,=\,\alpha \phi \left( \beta /\alpha \right)$ on 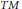$TM$ is an almost regular Landsberg metric, but not a Berwald metric.

Keywords

53B4053C60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1357 - 1374
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Asanov, G. S., Finsleroid-Finsler space with Berwald and Landsberg conditions. arXiv:math0603472.Google Scholar
[2] Asanov, G. S., Finsleroid-Finsler space and spray coefficients. arXiv:math0604526.Google Scholar
[3] Kitayama, M., Azuma, M., and Matsumoto, M., On Finsler spaces with (, )-metric. Regularity, geodesics and main scalars. J. Hokkaido Univ. Ed. Sect. II A 46(1995), 1–10.Google Scholar
[4] Kikuchi, S., On the condition that a space with (, )-metric be locally Minkowskian. Tensor 33(1979), no. 2, 242–246.Google Scholar
[5] Matsumoto, M., On Finsler spaces with Randers metric and special forms of important tensors. J. Math. Kyoto Univ.14(1974), 477–498.Google Scholar
[6] Matsumoto, M., Finsler spaces with (, )-metric of Douglas type. Tensor 60(1998), no. 2, 123–134.Google Scholar
[7] Shibata, C., Shimada, H., Azuma, M., and Yosuda, H., On Finsler spaces with Randers’ metric. Tensor 31(1977), no. 2, 219–226.Google Scholar
[8] Szabó, Z.I., Positive definite Berwald spaces. Structure theorems on Berwald spaces. Tensor 35(1981), no. 1, 25-39.Google Scholar