Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sandling, Robert
1974.
Group rings of circle and unit groups.
Mathematische Zeitschrift,
Vol. 140,
Issue. 3,
p.
195.
TAHARA, Ken-ichi
1977.
On the structure of <i>Q</i><sub>3</sub> (<i>G</i>) and the fourth dimension subgroups.
Japanese journal of mathematics. New series,
Vol. 3,
Issue. 2,
p.
381.
Losey, Gerald
and
Losey, Nora
1979.
Augmentation quotients of some nonabelian finite groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 85,
Issue. 2,
p.
261.
Losey, Gerald
and
Losey, Nora
1979.
The stable behavior of the augmentation quotients of the groups of order p3.
Journal of Algebra,
Vol. 60,
Issue. 2,
p.
337.
Sandling, Robert
and
Tahara, Ken-Ichi
1979.
Augmentation quotients of group rings and symmetric powers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 85,
Issue. 2,
p.
247.
Andrunakievich, V. A.
Arnautov, V. I.
Goyan, I. M.
and
Ryabukhin, Yu. M.
1980.
Associative rings.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 1,
p.
922.
Tahara, Ken-Ichi
1981.
The augmentation quotients of group rings and the fifth dimension subgroups.
Journal of Algebra,
Vol. 71,
Issue. 1,
p.
141.
Tahara, Ken-Ichi
1982.
Augmentation quotients and dimension subgroups of semidirect products.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 91,
Issue. 1,
p.
39.
Khambadkone, Meera
1983.
Subgroup ideals in grouprings I.
Journal of Pure and Applied Algebra,
Vol. 30,
Issue. 3,
p.
261.
HORIBE, Kazunori
and
TAHARA, Ken-Ichi
1984.
The stable behavior of the augmentation quotients of some groups of order <i>p</i><sup>4</sup>, I.
Japanese journal of mathematics. New series,
Vol. 10,
Issue. 1,
p.
137.
TAHARA, Ken-Ichi
and
YAMADA, Tsuneyo
1984.
The stable behavior of the augmentation quotients of some groups of order <i>p</i><sup>4</sup>, II.
Japanese journal of mathematics. New series,
Vol. 10,
Issue. 1,
p.
159.
Gupta, Narain
and
Tahara, Ken-Ichi
1985.
Dimension and lower central subgroups of metabelian p-groups.
Nagoya Mathematical Journal,
Vol. 100,
Issue. ,
p.
127.
PASSI, I. B. S.
SUCHETA
and
TAHARA, Ken-Ichi
1987.
Dimension subgroups and Schur multiplicator-III.
Japanese journal of mathematics. New series,
Vol. 13,
Issue. 2,
p.
371.
Gupta, Narain
1989.
Groups — Korea 1988.
Vol. 1398,
Issue. ,
p.
86.
TAHARA, Ken-Ichi
and
XIAO, Jian
1994.
On the seventh Lie dimension subgroups.
Japanese journal of mathematics. New series,
Vol. 20,
Issue. 1,
p.
199.
Sehgal, S.K.
2003.
Vol. 3,
Issue. ,
p.
455.


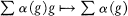 . Then Δ is a free abelian group with a free basis
. Then Δ is a free abelian group with a free basis 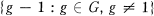 . A
. A