Article contents
Not Every K1-Embedded Subspace is K0-Embedded
Published online by Cambridge University Press: 20 November 2018
Extract
All topological spaces under discussion are assumed to be Tychonoff.
For any topological space X let τ(X) denote the topology of X. If X ᑕ Y then a function κ : τ(X) ⟶ τ(Y) is called an extender provided that κ(U) ∩ X = U for all U ∊ τ(X). In addition, X is said to be Kn-embedded in Y (cf. [3]) provided there is an extender κ : τ(X) ⟶ τ(Y) such that
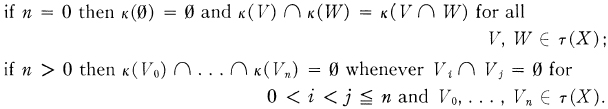
The extender κ is called a Kn-function (cf. [3]).
Eric van Douwen has asked whether there is a space X with a subspace Z which is Ki-embedded but not K0-embedded. The aim of this note is to answer this question.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1979
References
- 1
- Cited by


