Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Russo, Bernard
1977.
Banach Spaces of Analytic Functions.
Vol. 604,
Issue. ,
p.
94.
Klein, Abel
and
Russo, Bernard
1978.
Sharp inequalities for Weyl operators and Heisenberg groups.
Mathematische Annalen,
Vol. 235,
Issue. 2,
p.
175.
Russo, Bernard
1978.
The norm of the Lp-Fourier transform III compact extensions.
Journal of Functional Analysis,
Vol. 30,
Issue. 2,
p.
162.
Zhelobenko, D. P.
1981.
Harmonic analysis on reductive Lie groups.
Journal of Soviet Mathematics,
Vol. 15,
Issue. 4,
p.
490.
Andersson, Mats Erik
1998.
On the vector valued Hausdorff-Young inequality.
Arkiv för Matematik,
Vol. 36,
Issue. 1,
p.
1.
Baklouti, A.
Smaoui, K.
and
Ludwig, J.
2003.
Estimate of the Lp-Fourier transform norm on nilpotent Lie groups.
Journal of Functional Analysis,
Vol. 199,
Issue. 2,
p.
508.
Führ, Hartmut
2006.
Hausdorff–Young Inequalities for Group Extensions.
Canadian Mathematical Bulletin,
Vol. 49,
Issue. 4,
p.
549.
Baklouti, A.
Ludwig, J.
Scuto, L.
and
Smaoui, K.
2007.
Estimate of the L p -Fourier Transform Norm on Strong ✱-Regular Exponential Solvable Lie Groups.
Acta Mathematica Sinica, English Series,
Vol. 23,
Issue. 7,
p.
1173.
Baklouti, Ali
and
Inoue, Junko
2011.
Estimate of the Lp -Fourier transform norm for connected nilpotent Lie groups.
Advances in Pure and Applied Mathematics,
Vol. 2,
Issue. 3-4,
Baklouti, Ali
and
Inoue, Junko
2020.
The $$L^p$$-Fourier Transform Norm on Compact Extensions of Locally Compact Groups.
Journal of Fourier Analysis and Applications,
Vol. 26,
Issue. 2,
Satomi, Takashi
2023.
An Inequality for the Convolutions on Unimodular Locally Compact Groups and the Optimal Constant of Young’s Inequality.
Journal of Fourier Analysis and Applications,
Vol. 29,
Issue. 1,
Baklouti, Ali
and
Inoue, Junko
2024.
Harmonic Analysis and Partial Differential Equations.
p.
139.


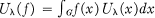 then
then
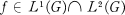 .
.