Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:39:17.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Nilpotent Groups in Which Every Product of Four Elements Can be Reordered

Published online by Cambridge University Press:  20 November 2018

M. Maj  and
S. E. Stonehewer
M. Maj
Affiliation:
Dipartimento Di Matematica Ed Applicazioni, Via Mezzocannone 8, 80134 Napoli, Italy
S. E. Stonehewer
Affiliation:
Mathematics Institute University of Warwick, Coventry CV4 7AL, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group and n(≧ 2) an integer. We say that G belongs to the class of groups Pn if every product of n elements can be reordered, i.e. for all n-tuples 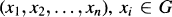, there exists a non-trivial element σ in the symmetric group Σn such that 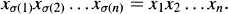Let P denote the union of the classes Pn, n ≧ 2. Clearly every finite group belongs to P and each class Pn is closed with respect to forming subgroups and factor groups.

Keywords

20F3420F99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 6 , 01 December 1990 , pp. 1053 - 1066
Copyright
Copyright © Canadian Mathematical Society 1990

Footnotes

The authors are grateful to British Council and C.N.R. for financial support while this work was being carried out in Italy and Warwick.

References

1. Bianchi, M., Brandi, R., Mauri, A. Gillio Berta, On the 4-permutational property, Arch. Math. 48 (1987), 281–285.Google Scholar
2. Curzio, M., Longobardi, P., Maj, M., Su di un problema combinatorio di teoria dei gruppi, Atti Ace. Lined Rend. Sci. Mat. Fis. Nat., 74 (1983), 136–142.Google Scholar
3. Curzio, M., Robinson, D.J.S., On a permutational property of groups, Arch, Math. 44 (1985), 385–389.Google Scholar
4. Higman, G., Rewriting products of group elements, Lectures given in Urbana in 1985 (unpublished).Google Scholar
5. Longobardi, P., Maj, M., On groups in which every product of four elements can be reordered, Arch. Math. 49 (1987), 273–276.Google Scholar
6. Scorza, G., I gruppi finiti che possono pensarsi come somma di tre loro sottogruppi, Boll. U.M.I. 5 (1926), 216–218.Google Scholar