Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T12:02:16.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-cocompact Group Actions and 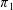$\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  26 June 2019

Ross Geoghegan ,
Craig Guilbault  and
Michael Mihalik
Ross Geoghegan
Affiliation:
Department of Mathematics, State University of New York-Binghamton, BinghamtonNY, USA Email: [email protected]
Craig Guilbault
Affiliation:
Department of Mathematics, University of Wisconsin-Milwaukee, MilwaukeeWI, USA Email: [email protected]
Michael Mihalik
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, TN, USA Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A finitely presented 1-ended group 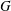$G$ has semistable fundamental group at infinity if 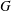$G$ acts geometrically on a simply connected and locally compact ANR 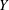$Y$ having the property that any two proper rays in 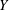$Y$ are properly homotopic. This property of 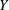$Y$ captures a notion of connectivity at infinity stronger than “1-ended”, and is in fact a feature of 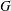$G$, being independent of choices. It is a fundamental property in the homotopical study of finitely presented groups. While many important classes of groups have been shown to have semistable fundamental group at infinity, the question of whether every 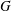$G$ has this property has been a recognized open question for nearly forty years. In this paper we attack the problem by considering a proper but non-cocompact action of a group 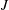$J$ on such an 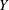$Y$. This 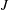$J$ would typically be a subgroup of infinite index in the geometrically acting over-group 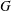$G$; for example 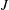$J$ might be infinite cyclic or some other subgroup whose semistability properties are known. We divide the semistability property of 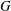$G$ into a 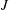$J$-part and a “perpendicular to 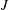$J$” part, and we analyze how these two parts fit together. Among other things, this analysis leads to a proof (in a companion paper) that a class of groups previously considered to be likely counter examples do in fact have the semistability property.

Keywords

finitely presented groupsemistability

MSC classification

Primary: 20F69: Asymptotic properties of groups
Secondary: 20F65: Geometric group theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 5 , October 2020 , pp. 1275 - 1303
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author C. G. was supported by Simons Foundation Grants 207264 & 427244, CRG.

References

Bestvina, M. and Mess, G., The boundary of negatively curved groups. J. Amer. Math. Soc. 4(1991), no. 3, 469–481. https://doi.org/10.2307/2939264CrossRefGoogle Scholar
Bowditch, B. H., Planar groups and the Seifert conjecture. J. Reine Angew. Math. 576(2004), 11–62. https://doi.org/10.1515/crll.2004.084Google Scholar
Conner, G. R. and Mihalik, M. L., Commensurated subgroups, semistability and simple connectivity at infinity. Algebr. Geom. Topol. 14(2014), no. 6, 3509–3532. https://doi.org/10.2140/agt.2014.14.3509CrossRefGoogle Scholar
Geoghegan, R., Topological methods in group theory. Graduate Texts in Mathematics, 243, Springer, New York, 2008. https://doi.org/10.1007/978-0-387-74614-2CrossRefGoogle Scholar
Geoghegan, R. and Guilbault, C. R., Topological properties of spaces admitting free group actions. J. Topol. 5(2012), no. 2, 249–275. https://doi.org/10.1112/jtopol/jts002CrossRefGoogle Scholar
Geoghegan, R., Guilbault, C., and Mihalik, M., Topological properties of spaces admitting a coaxial homeomorphism. Algebr. Geom. Topol., to appear. arxiv:1611.01807Google Scholar
Geoghegan, R. and Mihalik, M. L., The fundamental group at infinity. Topology 35(1996), no. 3, 655–669. https://doi.org/10.1016/0040-9383(95)00033-XCrossRefGoogle Scholar
Lee, R. and Raymond, F., Manifolds covered by Euclidean space. Topology 14(1975), 49–57. https://doi.org/10.1016/0040-9383(75)90034-8CrossRefGoogle Scholar
Mihalik, M. L., Bounded depth ascending HNN extensions and $\unicode[STIX]{x1D70B}_{1}$-semistability at infinity. arxiv:1709.09140Google Scholar
Mihalik, M. L., Semistability at the end of a group extension. Trans. Amer. Math. Soc. 277(1983), no. 1, 307–321. https://doi.org/10.2307/1999358CrossRefGoogle Scholar
Mihalik, M. L., Ends of groups with the integers as quotient. J. Pure Appl. Algebra 35(1985), no. 3, 305–320. https://doi.org/10.1016/0022-4049(85)90048-9CrossRefGoogle Scholar
Mihalik, M. L., Ends of double extension groups. Topology 25(1986), no. 1, 45–53. https://doi.org/10.1016/0040-9383(86)90004-2CrossRefGoogle Scholar
Mihalik, M. L., Semistability at ∞, ∞-ended groups and group cohomology. Trans. Amer. Math. Soc. 303(1987), no. 2, 479–485. https://doi.org/10.2307/2000678Google Scholar
Mihalik, M. L., Semistability and simple connectivity at infinity of a finitely generated group with a finite series of commensurated subgroups. Algebr. Geom. Topol. 16(2016), no. 6, 3615–3640. https://doi.org/10.2140/agt.2016.16.3615CrossRefGoogle Scholar
Mihalik, M. L. and Tschantz, S. T., One relator groups are semistable at infinity. Topology 31(1992), no. 4, 801–804. https://doi.org/10.1016/0040-9383(92)90010-FCrossRefGoogle Scholar
Mihalik, M. L. and Tschantz, S. T., Semistability of amalgamated products and HNN-extensions. Mem. Amer. Math. Soc. 98(1992), no. 471, vi+86. https://doi.org/10.1090/memo/0471Google Scholar
West, J. E., Mapping Hilbert cube manifolds to ANR’s: a solution of a conjecture of Borsuk. Ann. of Math. (2) 106(1977), no. 1, 1–18. https://doi.org/10.2307/1971155CrossRefGoogle Scholar
Wright, D. G., Contractible open manifolds which are not covering spaces. Topology 31(1992), no. 2, 281–291. https://doi.org/10.1016/0040-9383(92)90021-9CrossRefGoogle Scholar