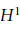 ${{H}^{1}}$ and the Étale Van Kampen Theorem
${{H}^{1}}$ and the Étale Van Kampen TheoremPublished online by Cambridge University Press: 20 November 2018
Generalized étale homotopy pro-groups  $\pi _{1}^{\acute{e}t}(C, x)$ associated with pointed, connected, small Grothendieck sites
$\pi _{1}^{\acute{e}t}(C, x)$ associated with pointed, connected, small Grothendieck sites 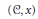 $(C, x)$ are defined, and their relationship to Galois theory and the theory of pointed torsors for discrete groups is explained.
$(C, x)$ are defined, and their relationship to Galois theory and the theory of pointed torsors for discrete groups is explained.
Applications include new rigorous proofs of some folklore results around 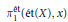 $\pi _{1}^{\acute{e}t}(\acute{e}t(X) x)$, a description of Grothendieck's short exact sequence for Galois descent in terms of pointed torsor trivializations, and a new étale van Kampen theorem that gives a simple statement about a pushout square of pro-groups that works for covering families that do not necessarily consist exclusively of monomorphisms. A corresponding van Kampen result for Grothendieck's profinite groups
$\pi _{1}^{\acute{e}t}(\acute{e}t(X) x)$, a description of Grothendieck's short exact sequence for Galois descent in terms of pointed torsor trivializations, and a new étale van Kampen theorem that gives a simple statement about a pushout square of pro-groups that works for covering families that do not necessarily consist exclusively of monomorphisms. A corresponding van Kampen result for Grothendieck's profinite groups 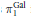 $\text{ }\!\!\pi\!\!\text{ }_{1}^{\text{Gal}}$ immediately follows.
$\text{ }\!\!\pi\!\!\text{ }_{1}^{\text{Gal}}$ immediately follows.