Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T23:39:08.139Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Abelian Generalizations of the Erdős-Kac Theorem

Published online by Cambridge University Press:  20 November 2018

M. Ram Murty  and
Filip Saidak
M. Ram Murty
Affiliation:
Department of Mathematics, Queen's University, Kingston, Ontario, K7L 3N6 e-mail: [email protected] e-mail: [email protected]
Filip Saidak
Affiliation:
Department of Mathematics, Queen's University, Kingston, Ontario, K7L 3N6 e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $a$ be a natural number greater than 1. Let 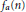${{f}_{a}}\left( n \right)$ be the order of 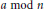$a\,\bmod \,n$. Denote by 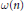$\omega \left( n \right)$ the number of distinct prime factors of $n$. Assuming a weak form of the generalised Riemann hypothesis, we prove the following conjecture of Erdös and Pomerance:

The number of 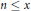$n\,\le \,x$ coprime to a satisfying

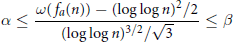$$\alpha \le \frac{\omega \left( {{f}_{a}}\left( n \right) \right)-{{\left( \log \,\log \,n \right)}^{2}}/2}{{{\left( \log \,\log \,n \right)}^{3/2}}/\sqrt{3}}\le \beta $$

is asymptotic to 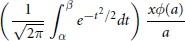$\left( \frac{1}{\sqrt{2\pi }}\int_{\alpha }^{\beta }{{{e}^{-{{t}^{2}}/2}}}dt \right)\frac{x\phi \left( a \right)}{a}$ as $x$ tends to infinity.

Keywords

11K3611K99Turán's theoremErdős-Kac theoremChebotarev density theoremErdős-Pomerance conjecture
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 2 , 01 April 2004 , pp. 356 - 372
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Deligne, P., Formes modulaires et représentations l-adiques. Sem. Bourbaki 355, Lecture Notes in Math. 179, 139–172, Springer Verlag, 1971.Google Scholar
[2] Elliott, P. D. T. A., Probabilistic Number Theory. Volume I. & II, Springer Verlag, 1979.Google Scholar
[3] Erdős, P., On the normal order of prime factors of p – 1 and some related problems concerning Euler's ϕ-function. Quart. J. Math. Oxford Ser. 6(1935), 205–213.Google Scholar
[4] Erdős, P. and Kac, M., The Gaussian law of errors in the theory of additive number theoretic functions. Amer. J. Math. 62(1940), 738–742.Google Scholar
[5] Erdős, P. and Pomerance, C., On the normal number of prime factors of ϕ(n). Rocky Mountain J. Math. 15(1985), 343–352.Google Scholar
[6] Halberstam, H., On the distribution of additive number-theoretic functions (I, II, III). J. London Math. Soc. 30(1955), 43–53; 31, 1–14; 31(1956), 15–27.Google Scholar
[7] Hardy, G. H. and Ramanujan, S., The normal number of prime factors of a number n. Quart. J. Math. 48(1917), 76–97.Google Scholar
[8] Kubilius, J., Probabilistic methods in number theory. Transl. Math. Monogr. 11, Rhode Island, 1964.Google Scholar
[9] Lagarias, J. and Odlyzko, A., Effective versions of the Tchebotarev density theorem. In: Algebraic Number Fields, (ed. Fröhlich, A.), Proceedings of the 1975 Durham Symposium, Academic Press, 1975.Google Scholar
[10] Lehmer, D. H., Ramanujan's function τ(n). Duke Math. J. 10(1943), 483–492.Google Scholar
[11] Lehmer, D. H., The vanishing of Ramanujan's function τ(n). Duke Math. J. 14(1947), 429–433.Google Scholar
[12] Murty, R., On Artin's conjecture. J. Number Theory 16(1983), 147–168.Google Scholar
[13] Murty, R., Problems in Analytic Number Theory. Springer Verlag 206, New York, 2001.Google Scholar
[14] Murty, V. K. and Murty, R. M., Prime divisors of Fourier coefficients of modular forms. Duke Math. J. 51(1984), 57–76.Google Scholar
[15] Murty, K. and Murty, R., An analogue of the Erdős-Kac theorem for Fourier coefficients of modular forms. Indian J. Pure Appl. Math. 15(1984), 1090–1101.Google Scholar
[16] Norton, K. K., On the number of restricted prime factors of an integer (I). Illinois J. Math. 20(1976), 681–705.Google Scholar
[17] Pomerance, C., On the distribution of amicable numbers. J. Reine Angew. Math. 293/294(1977), 217–222.Google Scholar
[18] Ramanujan, S., Highly composite numbers. Proc. LondonMath. Soc. (2) 14(1915), 347–409, see also Collected Works, Oxford, 1927.Google Scholar
[19] Saidak, F., An elementary proof of a theorem of Délange. Mathematical Reports of the Royal Society of Canada, 24(2002), 144–151.Google Scholar
[20] Saidak, F., Non-Abelian Generalizations of the Erdős-Kac Theorem. Ph.D. Thesis, Queen's University, Kingston, 2001.Google Scholar
[21] Saidak, F., Erdős-Kac type theorems for ω (fa (p)) and ωfa (p)) via higher moments. Acta Math. Univ. Com., submitted.Google Scholar
[22] Shapiro, H., Distribution functions of additive arithmetic functions. Proc. Nat. Acad. Sci. USA 42(1956), 426–430.Google Scholar
[23] Turán, P., On a theorem of Hardy and Ramanujan. J. LondonMath. Soc. 9(1934), 274–276.Google Scholar