Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T05:23:00.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent Orbits and Whittaker Functions for Derived Functor Modules of Sp(2, ℝ)

Published online by Cambridge University Press:  20 November 2018

Takuya Miyazaki
Takuya Miyazaki*
Affiliation:
Department of Mathematics, Keio University, 3-14-1 Hiyoshi, Kouhoku, Yokohama 223-8522, Japan, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the moderate growth generalized Whittaker functions, associated to a unitary character 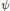$\psi $ of a unipotent subgroup, for the non-tempered cohomological representation of 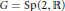$G\,=\,\text{Sp}\left( 2,\,\mathbb{R} \right)$. Through an explicit calculation of a holonomic system which characterizes these functions we observe that their existence is determined by the including relation between the real nilpotent coadjoint 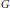$G$-orbit of 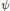$\psi $ in 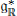$\mathfrak{g}_{\mathbb{R}}^{*}$ and the asymptotic support of the cohomological representation.

Keywords

22E4622E30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 4 , 01 August 2002 , pp. 769 - 794
Copyright
Copyright © Canadian Mathematical Society 2002

References

[B-V] Barbasch, D. and Vogan, D., The local structure of characters. J. Funct. Anal. 37 (1980), 27–55.Google Scholar
[Ba] Barchini, L., Szegö kernels associated with Zuckerman modules. J. Funct. Anal. 131 (1995), 145–182.Google Scholar
[D] Djoković, D. Z., Closures of conjugacy classes in classical real linear Lie groups. Algebra, Carbondale 1980, Proc. Conf., Southern Illinois Univ., Carbondale, Ill., 1980, Lecture Notes in Math. 848, 1981, 63–83.Google Scholar
[K] Kawanaka, N., Shintani lifting and Gelfand-Graev representations. Proc. Sympos. PureMath. 47 (1987), 147–163.Google Scholar
[Ko] Kostant, B., On Whittaker vectors and representation theory. Invent.Math. 48 (1978), 101–184.Google Scholar
[M-O-S] Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and Theorems for the special functions of Mathematical Physics, Third Edition. Die GrundlehrenMath.Wiss. Einzeldarstellungen 52, Springer-Verlag, 1966.Google Scholar
[Ma] Matumoto, H., C∞-Whittaker vectors corresponding to a principal nilpotent orbit of a real reductive linear Lie group, and wave front sets. Compositio Math. 82 (1992), 189–244.Google Scholar
[M] Miyazaki, T., The generalized Whittaker functions for Sp(2, R) and the gamma factor of the Andrianov L-function. J.Math. Sci. Tokyo 7 (2000), 241–295.Google Scholar
[N] Nöel, A., Nilpotent orbits and theta-stable parabolic subalgebras. Represent. Theory 2 (1998), 1–32.Google Scholar
[O] Oda, T., An explicit integral representation of Whittaker functions on Sp(2, R) for the large discrete series representations. Tôhoku Math. J. 46 (1994), 261–279.Google Scholar
[S-V] Schmid, W. and Vilonen, K., Characteristic cycles and wave front cycles of representations of reductive Lie groups. Ann. of Math. 151 (2000), 1071–1118.Google Scholar
[V1] Vogan, D. A., Associated varieties and unipotent representations. Harmonic Analysis on Reductive Groups, (eds.,W. Baker and P. Sally), Birkhäuser, Boston, Bassel, Berlin, 1991, 315–388.Google Scholar
[V2] Vogan, D. A., Gelfand-Kirillov dimension for Harish-Chandra modules. Invent.Math. 48 (1978), 75–98.Google Scholar
[W] Wong, H.-W., Dolbeault cohomological realization of Zuckerman modules associated with finite rank representations. J. Funct. Anal. 129 (1995), 428–454.Google Scholar
[Y1] Yamashita, H., Finite multiplicity theorems for induced representations of semisimple Lie groups I. J. Math. Kyoto Univ. 28 (1988), 173–211; II: Applications to generalized Gelfand-Graev representations, ibid. 28 (1988), 383–444.Google Scholar
[Y2] Yamashita, H., Cayley transform and generalized Whittaker models for irreducible highest weight modules. preprint.Google Scholar