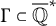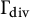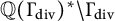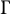1 Introduction
1.1 Rémond’s conjecture
Let
![]() $\alpha \in \overline {\mathbb {Q}}$
. The (absolute logarithmic) Weil height of
$\alpha \in \overline {\mathbb {Q}}$
. The (absolute logarithmic) Weil height of
![]() $\alpha $
is the real number
$\alpha $
is the real number
 $$\begin{align*}h(\alpha) = \frac{1}{[\mathbb{Q}(\alpha) : \mathbb{Q}]} \log\left(\vert lc(\alpha)\vert \prod_\sigma \max\{1, \vert \sigma\alpha\vert\}\right), \end{align*}$$
$$\begin{align*}h(\alpha) = \frac{1}{[\mathbb{Q}(\alpha) : \mathbb{Q}]} \log\left(\vert lc(\alpha)\vert \prod_\sigma \max\{1, \vert \sigma\alpha\vert\}\right), \end{align*}$$
where
![]() $lc(\alpha )$
denotes the leading coefficient of the minimal polynomial of
$lc(\alpha )$
denotes the leading coefficient of the minimal polynomial of
![]() $\alpha $
over
$\alpha $
over
![]() $\mathbb {Z}$
, and where
$\mathbb {Z}$
, and where
![]() $\sigma $
runs over all field embeddings
$\sigma $
runs over all field embeddings
![]() $\mathbb {Q}(\alpha ) \to \overline {\mathbb {Q}}$
. The function
$\mathbb {Q}(\alpha ) \to \overline {\mathbb {Q}}$
. The function
![]() $h : \overline {\mathbb {Q}} \to \mathbb {R}$
is nonnegative and vanishes precisely at
$h : \overline {\mathbb {Q}} \to \mathbb {R}$
is nonnegative and vanishes precisely at
![]() $\mu _\infty $
, the set of all roots of unity, and
$\mu _\infty $
, the set of all roots of unity, and
![]() $0$
by a theorem of Kronecker. It is also invariant under Galois conjugation and satisfies
$0$
by a theorem of Kronecker. It is also invariant under Galois conjugation and satisfies
![]() $h(\alpha ^n)=\vert n\vert h(\alpha )$
for all
$h(\alpha ^n)=\vert n\vert h(\alpha )$
for all
![]() $\alpha \in \overline {\mathbb {Q}}$
and all
$\alpha \in \overline {\mathbb {Q}}$
and all
![]() $n\in \mathbb {Z}$
. For more properties on h, see [Reference Bombieri and Gubler8].
$n\in \mathbb {Z}$
. For more properties on h, see [Reference Bombieri and Gubler8].
Let X be a set of algebraic numbers. We say that points of small height (or short, small points) of X lie in a set
![]() $Y\subset \overline {\mathbb {Q}}$
if there exists a positive constant c such that
$Y\subset \overline {\mathbb {Q}}$
if there exists a positive constant c such that
![]() $h(\alpha ) \geq c$
for all
$h(\alpha ) \geq c$
for all
![]() $\alpha \in X\backslash Y$
.
$\alpha \in X\backslash Y$
.
The case where small points of an algebraic field lie in
![]() $\mu _\infty \cup \{0\}$
has been intensively studied since the beginning of this century (see, for example, [Reference Amoroso, David and Zannier2, Reference Amoroso and Dvornicich3, Reference Amoroso and Zannier5, Reference Bombieri and Zannier9, Reference Fili and Milner11–Reference Grizzard14, Reference Habegger16, Reference Pazuki and Pengo18, Reference Plessis21, Reference Plessis22, Reference Sahu28]). For various technical reasons, it is difficult to adapt the ideas of these papers to locate small points of an algebraic field that are not contained in
$\mu _\infty \cup \{0\}$
has been intensively studied since the beginning of this century (see, for example, [Reference Amoroso, David and Zannier2, Reference Amoroso and Dvornicich3, Reference Amoroso and Zannier5, Reference Bombieri and Zannier9, Reference Fili and Milner11–Reference Grizzard14, Reference Habegger16, Reference Pazuki and Pengo18, Reference Plessis21, Reference Plessis22, Reference Sahu28]). For various technical reasons, it is difficult to adapt the ideas of these papers to locate small points of an algebraic field that are not contained in
![]() $\mu _\infty \cup \{0\}$
. As far as [Reference Amoroso1] shows, the first one who managed to do this is Amoroso in 2016, see our explanation below for more details.
$\mu _\infty \cup \{0\}$
. As far as [Reference Amoroso1] shows, the first one who managed to do this is Amoroso in 2016, see our explanation below for more details.
Consider the field
![]() $L=\mathbb {Q}(\mu _\infty , \alpha , \alpha ^{1/2},\alpha ^{1/3},\dots )$
, where
$L=\mathbb {Q}(\mu _\infty , \alpha , \alpha ^{1/2},\alpha ^{1/3},\dots )$
, where
![]() $\alpha \in \overline {\mathbb {Q}}^*$
. It is trivial to construct small points in
$\alpha \in \overline {\mathbb {Q}}^*$
. It is trivial to construct small points in
![]() $L^*$
. For instance, we have all roots of unity, but also
$L^*$
. For instance, we have all roots of unity, but also
![]() $\alpha ^{1/n}$
with n large enough since
$\alpha ^{1/n}$
with n large enough since
![]() $h(\alpha ^{1/n})=h(\alpha )/n$
. But does
$h(\alpha ^{1/n})=h(\alpha )/n$
. But does
![]() $L^*$
also contain nonobvious small points; i.e., elements of small height not in
$L^*$
also contain nonobvious small points; i.e., elements of small height not in
![]() $\{\zeta \alpha ^q, \zeta \in \mu _\infty , q\in \mathbb {Q}\}$
? By a result of Amoroso and Dvornicich [Reference Amoroso and Dvornicich3], the answer is no if
$\{\zeta \alpha ^q, \zeta \in \mu _\infty , q\in \mathbb {Q}\}$
? By a result of Amoroso and Dvornicich [Reference Amoroso and Dvornicich3], the answer is no if
![]() $\alpha \in \mu _\infty $
. But this question is still open for
$\alpha \in \mu _\infty $
. But this question is still open for
![]() $\alpha \notin \mu _\infty $
. A very particular case of a deep and recent conjecture of Rémond, related to the Zilber–Pink conjecture, predicts a negative answer to this question (see Conjecture 1.1).
$\alpha \notin \mu _\infty $
. A very particular case of a deep and recent conjecture of Rémond, related to the Zilber–Pink conjecture, predicts a negative answer to this question (see Conjecture 1.1).
Throughout this introduction,
![]() $\Gamma $
always denotes a finitely generated subgroup of
$\Gamma $
always denotes a finitely generated subgroup of
![]() $\overline {\mathbb {Q}}^*$
. Define
$\overline {\mathbb {Q}}^*$
. Define
![]() $\Gamma _{\mathrm {div}}$
as the division group of
$\Gamma _{\mathrm {div}}$
as the division group of
![]() $\Gamma $
, i.e., the set of
$\Gamma $
, i.e., the set of
![]() $\gamma \in \overline {\mathbb {Q}}^*$
for which there exists an integer
$\gamma \in \overline {\mathbb {Q}}^*$
for which there exists an integer
![]() $n\in \mathbb {N}=\{1,2,\dots \}$
satisfying
$n\in \mathbb {N}=\{1,2,\dots \}$
satisfying
![]() $\gamma ^n\in \Gamma $
.
$\gamma ^n\in \Gamma $
.
Conjecture 1.1 (Rémond [Reference Rémond27, Conjecture 3.4])
Let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup.
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup.
-
(i) (Strong form): There is a positive constant c such that
 $$ \begin{align*} h(\alpha) \geq \frac{c}{[\mathbb{Q}(\Gamma_{\mathrm{div}},\alpha) : \mathbb{Q}(\Gamma_{\mathrm{div}})]} \; \text{for all} \; \alpha\in \overline{\mathbb{Q}}^*\backslash \Gamma_{\mathrm{div}}. \end{align*} $$
$$ \begin{align*} h(\alpha) \geq \frac{c}{[\mathbb{Q}(\Gamma_{\mathrm{div}},\alpha) : \mathbb{Q}(\Gamma_{\mathrm{div}})]} \; \text{for all} \; \alpha\in \overline{\mathbb{Q}}^*\backslash \Gamma_{\mathrm{div}}. \end{align*} $$
-
(ii) (Weak form): For any
 $\varepsilon>0$
, there exists a positive constant
$\varepsilon>0$
, there exists a positive constant
 $c_\varepsilon $
such that
$c_\varepsilon $
such that  $$ \begin{align*} h(\alpha)\geq \frac{c_\varepsilon}{[\mathbb{Q}(\Gamma_{\mathrm{div}},\alpha) : \mathbb{Q}(\Gamma_{\mathrm{div}})]^{1+\varepsilon}} \; \text{for all} \; \alpha\in \overline{\mathbb{Q}}^*\backslash \Gamma_{\mathrm{div}}. \end{align*} $$
$$ \begin{align*} h(\alpha)\geq \frac{c_\varepsilon}{[\mathbb{Q}(\Gamma_{\mathrm{div}},\alpha) : \mathbb{Q}(\Gamma_{\mathrm{div}})]^{1+\varepsilon}} \; \text{for all} \; \alpha\in \overline{\mathbb{Q}}^*\backslash \Gamma_{\mathrm{div}}. \end{align*} $$
-
(iii) (Degree one form): Small points of
 $\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
lie in
$\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
lie in
 $\Gamma _{\mathrm {div}}$
.
$\Gamma _{\mathrm {div}}$
.
The reader interested on recent advances concerning Rémond’s conjecture is referred to [Reference Amoroso1, Reference Grizzard15, Reference Plessis23, Reference Plessis24, Reference Pottmeyer26, Reference Rémond27].
Write
![]() $\langle X\rangle $
for the group generated by a set
$\langle X\rangle $
for the group generated by a set
![]() $X\subset \overline {\mathbb {Q}}^*$
. We clearly have the implications
$X\subset \overline {\mathbb {Q}}^*$
. We clearly have the implications
![]() $(i) \Rightarrow (ii) \Rightarrow (iii)$
. The strong form generalizes the relative Lehmer’s problem, which corresponds to the case
$(i) \Rightarrow (ii) \Rightarrow (iii)$
. The strong form generalizes the relative Lehmer’s problem, which corresponds to the case
![]() $\Gamma = \{1\}$
. As far as [Reference Amoroso and Dvornicich3] and [Reference Amoroso and Zannier4] show, the strong form is not yet known in any situation and both the weak form and the degree one form are only known when
$\Gamma = \{1\}$
. As far as [Reference Amoroso and Dvornicich3] and [Reference Amoroso and Zannier4] show, the strong form is not yet known in any situation and both the weak form and the degree one form are only known when
![]() $\Gamma $
is trivial. The first partial result going in the direction of Conjecture 1.1 for nontrivial groups was given by Amoroso. He proved that small points of
$\Gamma $
is trivial. The first partial result going in the direction of Conjecture 1.1 for nontrivial groups was given by Amoroso. He proved that small points of
![]() $\mathbb {Q}(\zeta _3, 2^{1/3}, \zeta _{3^2}, 2^{1/3^2},\dots )^*$
, with
$\mathbb {Q}(\zeta _3, 2^{1/3}, \zeta _{3^2}, 2^{1/3^2},\dots )^*$
, with
![]() $\zeta _n=e^{2i\pi /n}$
, lie in
$\zeta _n=e^{2i\pi /n}$
, lie in
![]() $\langle 2\rangle _{\mathrm {div}}$
[Reference Amoroso1, Theorem 1.3]. The author then proved the same assertion by replacing
$\langle 2\rangle _{\mathrm {div}}$
[Reference Amoroso1, Theorem 1.3]. The author then proved the same assertion by replacing
![]() $2$
with
$2$
with
![]() $\alpha \in \mathbb {Q}^*$
and
$\alpha \in \mathbb {Q}^*$
and
![]() $3$
with a rational prime
$3$
with a rational prime
![]() $p>2$
[Reference Plessis23, Théorème 1.8].
$p>2$
[Reference Plessis23, Théorème 1.8].
The proof of these last two results relies on the “classical method,” i.e., the one to treat the case where small points of an algebraic field lie in
![]() $\mu _\infty \cup \{0\}$
. As already implied in [Reference Amoroso1, Remark 3.4], it seems that this method is (very) limited to handle Conjecture 1.1
$\mu _\infty \cup \{0\}$
. As already implied in [Reference Amoroso1, Remark 3.4], it seems that this method is (very) limited to handle Conjecture 1.1
![]() $(iii)$
, which explains why it is still largely open. So we need to tackle this conjecture from a totally different angle. We suggest a new one below.
$(iii)$
, which explains why it is still largely open. So we need to tackle this conjecture from a totally different angle. We suggest a new one below.
1.2 Presentation of results
Let
![]() $(y_n)$
be a sequence of
$(y_n)$
be a sequence of
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
$\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
![]() $h(y_n)\to 0$
. From Bilu’s equidistribution theorem [Reference Bilu6], it is not hard to check that
$h(y_n)\to 0$
. From Bilu’s equidistribution theorem [Reference Bilu6], it is not hard to check that
 $$\begin{align*}\frac{\# \{\sigma : \mathbb{Q}(y_n)\hookrightarrow \overline{\mathbb{Q}}, \; 1-\varepsilon\leq \vert \sigma y_n \vert\leq 1+\varepsilon\}}{[\mathbb{Q}(y_n) : \mathbb{Q}]} \underset{n\to+\infty}{\longrightarrow} 1 \end{align*}$$
$$\begin{align*}\frac{\# \{\sigma : \mathbb{Q}(y_n)\hookrightarrow \overline{\mathbb{Q}}, \; 1-\varepsilon\leq \vert \sigma y_n \vert\leq 1+\varepsilon\}}{[\mathbb{Q}(y_n) : \mathbb{Q}]} \underset{n\to+\infty}{\longrightarrow} 1 \end{align*}$$
for all
![]() $\varepsilon>0$
(if the sequence of terms
$\varepsilon>0$
(if the sequence of terms
![]() $[\mathbb {Q}(y_n) : \mathbb {Q}]$
is bounded, then
$[\mathbb {Q}(y_n) : \mathbb {Q}]$
is bounded, then
![]() $y_n\in \mu _\infty $
for all n large enough by Northcott’s theorem, and so the ratio above is
$y_n\in \mu _\infty $
for all n large enough by Northcott’s theorem, and so the ratio above is
![]() $1$
for all n large enough). In other words, if the Weil height of
$1$
for all n large enough). In other words, if the Weil height of
![]() $y_n$
is small enough, then “most of” its Galois conjugates over
$y_n$
is small enough, then “most of” its Galois conjugates over
![]() $\mathbb {Q}$
are “close” to the unit circle. Nonetheless, as
$\mathbb {Q}$
are “close” to the unit circle. Nonetheless, as
![]() $K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )$
is not a number field, Bilu’s theorem above cannot tell anything about the location in the complex plane of Galois conjugates of
$K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )$
is not a number field, Bilu’s theorem above cannot tell anything about the location in the complex plane of Galois conjugates of
![]() $y_n$
over
$y_n$
over
![]() $K_\Gamma $
. Our results stipulate that a fairly precise knowledge of the distribution of these numbers allows us to solve a part of Conjecture 1.1
$K_\Gamma $
. Our results stipulate that a fairly precise knowledge of the distribution of these numbers allows us to solve a part of Conjecture 1.1
![]() $(iii)$
. In Section 3, we will prove a result reducing the study of Conjecture 1.1
$(iii)$
. In Section 3, we will prove a result reducing the study of Conjecture 1.1
![]() $(iii)$
to the case that for all n large enough, “most of” Galois conjugates of
$(iii)$
to the case that for all n large enough, “most of” Galois conjugates of
![]() $y_n$
over
$y_n$
over
![]() $K_\Gamma $
are “close” to the unit circle.
$K_\Gamma $
are “close” to the unit circle.
Let
![]() $\alpha \in \overline {\mathbb {Q}}$
, and let
$\alpha \in \overline {\mathbb {Q}}$
, and let
![]() $\varepsilon>0$
. We write
$\varepsilon>0$
. We write
![]() $O_\Gamma (\alpha )$
for the orbit of
$O_\Gamma (\alpha )$
for the orbit of
![]() $\alpha $
under
$\alpha $
under
![]() $\mathrm {Gal}(\overline {\mathbb {Q}}/K_\Gamma )$
and we put
$\mathrm {Gal}(\overline {\mathbb {Q}}/K_\Gamma )$
and we put
 $$\begin{align*}d_{\Gamma, \varepsilon}(\alpha):= \frac{\# \{x\in O_\Gamma(\alpha), 1-\varepsilon\leq \vert x \vert^2\leq 1+\varepsilon\}}{\# O_\Gamma(\alpha)}. \end{align*}$$
$$\begin{align*}d_{\Gamma, \varepsilon}(\alpha):= \frac{\# \{x\in O_\Gamma(\alpha), 1-\varepsilon\leq \vert x \vert^2\leq 1+\varepsilon\}}{\# O_\Gamma(\alpha)}. \end{align*}$$
Theorem 1.2 Let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup. Then Conjecture 1.1
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup. Then Conjecture 1.1
![]() $(iii)$
is equivalent to the following assertion: Let
$(iii)$
is equivalent to the following assertion: Let
![]() $(y_n)$
be a sequence of
$(y_n)$
be a sequence of
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
$\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
![]() $h(y_n)\to 0$
. Assume that
$h(y_n)\to 0$
. Assume that
![]() $d_{\Gamma , \varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma , \varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
. Then
$\varepsilon>0$
. Then
![]() $y_n\in \Gamma _{\mathrm {div}}$
for all n large enough.
$y_n\in \Gamma _{\mathrm {div}}$
for all n large enough.
The length of an element
![]() $x\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
is defined to be the smallest integer
$x\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
is defined to be the smallest integer
![]() $l\in \mathbb {N}$
for which x can express as
$l\in \mathbb {N}$
for which x can express as
![]() $x= \sum _{j=1}^l x_j \gamma _j$
with
$x= \sum _{j=1}^l x_j \gamma _j$
with
![]() $x_j\in K_\Gamma $
and
$x_j\in K_\Gamma $
and
![]() $\gamma _j\in \Gamma _{\mathrm {div}}$
. Each element of
$\gamma _j\in \Gamma _{\mathrm {div}}$
. Each element of
![]() $\Gamma _{\mathrm {div}}$
has length
$\Gamma _{\mathrm {div}}$
has length
![]() $1$
. For
$1$
. For
![]() $N\in \mathbb {N}$
, put
$N\in \mathbb {N}$
, put
![]() $l_N(\Gamma )$
the set of elements of
$l_N(\Gamma )$
the set of elements of
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})$
with length
$\mathbb {Q}(\Gamma _{\mathrm {div}})$
with length
![]() $\leq N$
.
$\leq N$
.
From Theorem 1.2, it is enough to prove the following two conjectures to deduce Conjecture 1.1
![]() $(iii)$
.
$(iii)$
.
Conjecture 1.3 Let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, and let
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, and let
![]() $(y_n)$
be a sequence of
$(y_n)$
be a sequence of
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
$\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
![]() $h(y_n)\to 0$
and
$h(y_n)\to 0$
and
![]() $d_{\Gamma ,\varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma ,\varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
. Then there exists
$\varepsilon>0$
. Then there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $y_n\in l_N(\Gamma )$
for all n large enough.
$y_n\in l_N(\Gamma )$
for all n large enough.
Conjecture 1.4 Let
![]() $N\in \mathbb {N}$
, and let
$N\in \mathbb {N}$
, and let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup. Let
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup. Let
![]() $(y_n)$
be a sequence of
$(y_n)$
be a sequence of
![]() $l_N(\Gamma )\backslash \{0\}$
such that
$l_N(\Gamma )\backslash \{0\}$
such that
![]() $h(y_n)\to 0$
and
$h(y_n)\to 0$
and
![]() $d_{\Gamma ,\varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma ,\varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
. Then
$\varepsilon>0$
. Then
![]() $y_n\in \Gamma _{\mathrm {div}}$
for all n large enough.
$y_n\in \Gamma _{\mathrm {div}}$
for all n large enough.
Conjecture 1.4 with
![]() $N=1$
was solved by Rémond, see Lemma 1.5. Conjectures 1.1
$N=1$
was solved by Rémond, see Lemma 1.5. Conjectures 1.1
![]() $(iii)$
and 1.3 with
$(iii)$
and 1.3 with
![]() $N=1$
are therefore equivalent. However, this does not remove the interest of Conjecture 1.4 because Conjecture 1.3 could be easier to show when N is large.
$N=1$
are therefore equivalent. However, this does not remove the interest of Conjecture 1.4 because Conjecture 1.3 could be easier to show when N is large.
Both conjectures seem to be treated separately. Hence, we focus in this article on the second one only.
For a set X of algebraic numbers, write
![]() $X.\Gamma _{\mathrm {div}}$
for the set of
$X.\Gamma _{\mathrm {div}}$
for the set of
![]() $x\gamma $
with
$x\gamma $
with
![]() $x\in X$
and
$x\in X$
and
![]() $\gamma \in \Gamma _{\mathrm {div}}$
. Note that
$\gamma \in \Gamma _{\mathrm {div}}$
. Note that
![]() $l_1(\Gamma )= K_\Gamma .\Gamma _{\mathrm {div}}$
. The rank of an abelian group G is given by the maximal number of linearly independent elements in G. Note that
$l_1(\Gamma )= K_\Gamma .\Gamma _{\mathrm {div}}$
. The rank of an abelian group G is given by the maximal number of linearly independent elements in G. Note that
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma _{\mathrm {div}}$
have the same rank.
$\Gamma _{\mathrm {div}}$
have the same rank.
Lemma 1.5 (Rémond)
Let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, and let
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, and let
![]() $F/K_\Gamma $
be a finite extension. Then small points of
$F/K_\Gamma $
be a finite extension. Then small points of
![]() $F^*.\Gamma _{\mathrm {div}}$
lie in
$F^*.\Gamma _{\mathrm {div}}$
lie in
![]() $\Gamma _{\mathrm {div}}$
.
$\Gamma _{\mathrm {div}}$
.
Proof By Amoroso and Zannier’s result [Reference Amoroso and Zannier5, Theorem 1.2], small points of
![]() $F^*$
lie in
$F^*$
lie in
![]() $\mu _\infty \subset \Gamma _{\mathrm {div}}$
. By assumption,
$\mu _\infty \subset \Gamma _{\mathrm {div}}$
. By assumption,
![]() $\Gamma \subset \Gamma _{\mathrm {div}} \cap F^*\subset \Gamma _{\mathrm {div}}$
. Thus
$\Gamma \subset \Gamma _{\mathrm {div}} \cap F^*\subset \Gamma _{\mathrm {div}}$
. Thus
![]() $\Gamma , \Gamma _{\mathrm {div}}\cap F^*$
and
$\Gamma , \Gamma _{\mathrm {div}}\cap F^*$
and
![]() $\Gamma _{\mathrm {div}}$
all have the same rank, which is finite since
$\Gamma _{\mathrm {div}}$
all have the same rank, which is finite since
![]() $\Gamma $
is finitely generated. For
$\Gamma $
is finitely generated. For
![]() $a\in F$
, set
$a\in F$
, set
Thanks to a result of Rémond [Reference Pottmeyer26, Corollary 2.3], there is a positive constant c such that
![]() $h_{\Gamma }(a)\geq c$
for all
$h_{\Gamma }(a)\geq c$
for all
![]() $a\in F^*\backslash \Gamma _{\mathrm {div}}$
.
$a\in F^*\backslash \Gamma _{\mathrm {div}}$
.
Let
![]() $y= a\gamma \in F^*.\Gamma _{\mathrm {div}}$
, where
$y= a\gamma \in F^*.\Gamma _{\mathrm {div}}$
, where
![]() $a\in F^*$
and
$a\in F^*$
and
![]() $\gamma \in \Gamma _{\mathrm {div}}$
, such that
$\gamma \in \Gamma _{\mathrm {div}}$
, such that
![]() $h(y)<c$
. As
$h(y)<c$
. As
![]() $c> h(y)\geq h_{\Gamma }(a)$
, we get
$c> h(y)\geq h_{\Gamma }(a)$
, we get
![]() $a\in \Gamma _{\mathrm {div}}$
by the foregoing. The lemma follows.
$a\in \Gamma _{\mathrm {div}}$
by the foregoing. The lemma follows.
Remark 1.6 This lemma can be made quantitative since [Reference Amoroso and Zannier5, Theorem 1.2] and [Reference Pottmeyer26, Corollary 2.3] are.
Among all our theorems, the next one is the most difficult (and technical) to show. Hence, we will prove it at the end of this paper, that is in Section 8.
Theorem 1.7 Let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, let
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, let
![]() $N\in \mathbb {N}$
, and let
$N\in \mathbb {N}$
, and let
![]() $(y_n)$
be a sequence of
$(y_n)$
be a sequence of
![]() $l_N(\Gamma )$
. Assume that
$l_N(\Gamma )$
. Assume that
![]() $d_{\Gamma , \varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma , \varepsilon }(y_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
. Then for all
$\varepsilon>0$
. Then for all
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
![]() $d_{\Gamma , \varepsilon }(y_n)=1$
for all n large enough.
$d_{\Gamma , \varepsilon }(y_n)=1$
for all n large enough.
Remark 1.8 The proof of this theorem does not hold if we study the Galois conjugates of
![]() $y_n$
over
$y_n$
over
![]() $\mathbb {Q}$
(or
$\mathbb {Q}$
(or
![]() $\mathbb {Q}(\Gamma )$
) instead of
$\mathbb {Q}(\Gamma )$
) instead of
![]() $K_\Gamma $
. The reason is that we will use Kummer theory and for this, it is primordial that our ground field contains all roots of unity.
$K_\Gamma $
. The reason is that we will use Kummer theory and for this, it is primordial that our ground field contains all roots of unity.
Theorem 1.7 means that if “most of” elements in
![]() $O_\Gamma (y_n)$
are “close” to the unit circle, then they all are. Note that this theorem holds regardless of the value of
$O_\Gamma (y_n)$
are “close” to the unit circle, then they all are. Note that this theorem holds regardless of the value of
![]() $h(y_n)$
, which leads to the following natural question: How are the elements of
$h(y_n)$
, which leads to the following natural question: How are the elements of
![]() $O_\Gamma (y_n)$
scattered around the unit circle when
$O_\Gamma (y_n)$
scattered around the unit circle when
![]() $h(y_n)$
is small enough ? We predict they are concyclic and located on a circle centered at the origin. If it checks out, then Conjecture 1.4 would immediately fall thanks to our next theorem, a proof of which is given in Section 5.
$h(y_n)$
is small enough ? We predict they are concyclic and located on a circle centered at the origin. If it checks out, then Conjecture 1.4 would immediately fall thanks to our next theorem, a proof of which is given in Section 5.
Denote by
![]() $U(\Gamma )$
the set of algebraic numbers
$U(\Gamma )$
the set of algebraic numbers
![]() $\alpha $
such that the elements of
$\alpha $
such that the elements of
![]() $O_\Gamma (\alpha )$
are concyclic and located on a circle centered at the origin. Check that
$O_\Gamma (\alpha )$
are concyclic and located on a circle centered at the origin. Check that
![]() $\Gamma _{\mathrm {div}}$
is a subgroup of
$\Gamma _{\mathrm {div}}$
is a subgroup of
![]() $U(\Gamma )$
: Let
$U(\Gamma )$
: Let
![]() $x\in \Gamma _{\mathrm {div}}$
, and let
$x\in \Gamma _{\mathrm {div}}$
, and let
![]() $\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}/K_\Gamma )$
. By definition of the division group, we have
$\sigma \in \mathrm {Gal}(\overline {\mathbb {Q}}/K_\Gamma )$
. By definition of the division group, we have
![]() $x^n\in \Gamma $
for some
$x^n\in \Gamma $
for some
![]() $n\in \mathbb {Z}\backslash \{0\}$
. Thus
$n\in \mathbb {Z}\backslash \{0\}$
. Thus
![]() $\sigma (x^n)=x^n$
implying
$\sigma (x^n)=x^n$
implying
![]() $\vert \sigma x\vert = \vert x\vert $
; whence
$\vert \sigma x\vert = \vert x\vert $
; whence
![]() $x\in U(\Gamma )$
.
$x\in U(\Gamma )$
.
Theorem 1.9 Let
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, and let
$\Gamma \subset \overline {\mathbb {Q}}^*$
be a finitely generated subgroup, and let
![]() $N\in \mathbb {N}$
. Then small points of
$N\in \mathbb {N}$
. Then small points of
![]() $l_N(\Gamma )\cap U(\Gamma )$
lie in
$l_N(\Gamma )\cap U(\Gamma )$
lie in
![]() $\Gamma _{\mathrm {div}}$
.
$\Gamma _{\mathrm {div}}$
.
Remark 1.10 Theorem 1.9 can be made quantitative by using the arguments of this paper (see Remark 5.3 for details).
End this section by providing a collection of
![]() $\Gamma $
for which small points of
$\Gamma $
for which small points of
![]() $l_N(\Gamma )\backslash \{0\}$
lie in
$l_N(\Gamma )\backslash \{0\}$
lie in
![]() $U(\Gamma )$
, thus giving credit to our approach to attack Conjecture 1.1
$U(\Gamma )$
, thus giving credit to our approach to attack Conjecture 1.1
![]() $(iii)$
.
$(iii)$
.
A CM-field is a totally imaginary quadratic extension of a totally real field. The maximal totally real field extension
![]() $\mathbb {Q}^{tr}$
of
$\mathbb {Q}^{tr}$
of
![]() $\mathbb {Q}$
having only one quadratic extension, namely
$\mathbb {Q}$
having only one quadratic extension, namely
![]() $\mathbb {Q}^{tr}(i)$
, the CM-fields are therefore the subfields of
$\mathbb {Q}^{tr}(i)$
, the CM-fields are therefore the subfields of
![]() $\mathbb {Q}^{tr}(i)$
that are not totally real. In particular, a compositum of CM-fields is a CM-field. The classification of CM-number fields was made in [Reference Blanksby and Loxton7]; these are the fields of the form
$\mathbb {Q}^{tr}(i)$
that are not totally real. In particular, a compositum of CM-fields is a CM-field. The classification of CM-number fields was made in [Reference Blanksby and Loxton7]; these are the fields of the form
![]() $\mathbb {Q}(\alpha )$
with
$\mathbb {Q}(\alpha )$
with
![]() $\alpha \in U\backslash \{\pm 1\}$
, where U denotes the set of algebraic numbers with all its conjugates over
$\alpha \in U\backslash \{\pm 1\}$
, where U denotes the set of algebraic numbers with all its conjugates over
![]() $\mathbb {Q}$
on the unit circle. Note that if
$\mathbb {Q}$
on the unit circle. Note that if
![]() $\Gamma \subset U$
, then
$\Gamma \subset U$
, then
![]() $\Gamma _{\mathrm {div}}\subset U$
. The field
$\Gamma _{\mathrm {div}}\subset U$
. The field
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})$
is therefore a CM-field since it is the compositum of all
$\mathbb {Q}(\Gamma _{\mathrm {div}})$
is therefore a CM-field since it is the compositum of all
![]() $\mathbb {Q}(\alpha )$
with
$\mathbb {Q}(\alpha )$
with
![]() $\alpha \in \Gamma _{\mathrm {div}}\backslash \{\pm 1\}$
.
$\alpha \in \Gamma _{\mathrm {div}}\backslash \{\pm 1\}$
.
Corollary 1.11 Let
![]() $\Gamma \subset U$
be a finitely generated subgroup, and let
$\Gamma \subset U$
be a finitely generated subgroup, and let
![]() $N\in \mathbb {N}$
. Then small points of
$N\in \mathbb {N}$
. Then small points of
![]() $l_N(\Gamma )\backslash \{0\}$
lie in
$l_N(\Gamma )\backslash \{0\}$
lie in
![]() $\Gamma _{\mathrm {div}}$
.
$\Gamma _{\mathrm {div}}$
.
Proof By a theorem of Schinzel [Reference Schinzel29, Theorem 2], see also [Reference Pottmeyer25], small points of
![]() $\mathbb {Q}^{tr}(i)^*$
lie in U. As
$\mathbb {Q}^{tr}(i)^*$
lie in U. As
![]() $\Gamma \subset U$
, the field
$\Gamma \subset U$
, the field
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})$
is a CM-field; whence
$\mathbb {Q}(\Gamma _{\mathrm {div}})$
is a CM-field; whence
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})\subset \mathbb {Q}^{tr}(i)$
. Small points of
$\mathbb {Q}(\Gamma _{\mathrm {div}})\subset \mathbb {Q}^{tr}(i)$
. Small points of
![]() $l_N(\Gamma )\backslash \{0\}$
therefore lie in U. The corollary now arises from Theorem 1.9 since
$l_N(\Gamma )\backslash \{0\}$
therefore lie in U. The corollary now arises from Theorem 1.9 since
![]() $U \subset U(\Gamma )$
by definition.
$U \subset U(\Gamma )$
by definition.
Conjectures 1.1
![]() $(iii)$
and 1.3 are therefore equivalent for CM-fields. This corollary is the second partial result going in the direction of Conjecture 1.1
$(iii)$
and 1.3 are therefore equivalent for CM-fields. This corollary is the second partial result going in the direction of Conjecture 1.1
![]() $(iii)$
, and the first one of this form.
$(iii)$
, and the first one of this form.
2 Kummer theory
Fix once and for all a finitely generated subgroup
![]() $\Gamma \subset \overline {\mathbb {Q}}^*$
of rank b. As Conjecture 1.1
$\Gamma \subset \overline {\mathbb {Q}}^*$
of rank b. As Conjecture 1.1
![]() $(iii)$
, and therefore Conjecture 1.4, is true for
$(iii)$
, and therefore Conjecture 1.4, is true for
![]() $b=0$
(see the introduction), we can reduce the proof of all theorems mentioned in the introduction to the case that
$b=0$
(see the introduction), we can reduce the proof of all theorems mentioned in the introduction to the case that
![]() $b>0$
. We also fix once and for all a generating set
$b>0$
. We also fix once and for all a generating set
![]() $\mathcal {F}=\{\alpha _1,\dots ,\alpha _b\}$
of the torsion-free part of
$\mathcal {F}=\{\alpha _1,\dots ,\alpha _b\}$
of the torsion-free part of
![]() $\Gamma $
. Finally, for
$\Gamma $
. Finally, for
![]() $n\in \mathbb {N}$
, we put
$n\in \mathbb {N}$
, we put
![]() $\mathcal {F}^{1/n}=\{\alpha _1^{1/n},\dots ,\alpha _b^{1/n}\}$
and we define
$\mathcal {F}^{1/n}=\{\alpha _1^{1/n},\dots ,\alpha _b^{1/n}\}$
and we define
![]() $\mu _n$
as the set of roots of unity killed by n.
$\mu _n$
as the set of roots of unity killed by n.
Let n be a positive integer dividing
![]() $m\in \mathbb {N}\cup \{\infty \}$
(by convention, all integers divide
$m\in \mathbb {N}\cup \{\infty \}$
(by convention, all integers divide
![]() $\infty $
). Galois theory claims that
$\infty $
). Galois theory claims that
![]() $\mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F}^{1/n})/\mathbb {Q}(\mathcal {F}))$
is isomorphic to the inner semidirect product of
$\mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F}^{1/n})/\mathbb {Q}(\mathcal {F}))$
is isomorphic to the inner semidirect product of
![]() $\mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F})/\mathbb {Q}(\mathcal {F}))$
and
$\mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F})/\mathbb {Q}(\mathcal {F}))$
and
![]() $\mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F}^{1/n})/\mathbb {Q}(\mu _m, \mathcal {F}))$
. Thus each element
$\mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F}^{1/n})/\mathbb {Q}(\mu _m, \mathcal {F}))$
. Thus each element
![]() $\sigma \in \mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F}^{1/n})/\mathbb {Q}(\mathcal {F}))$
can be identified with a pair
$\sigma \in \mathrm {Gal}(\mathbb {Q}(\mu _m, \mathcal {F}^{1/n})/\mathbb {Q}(\mathcal {F}))$
can be identified with a pair
Concretely, if
![]() $x=\sum _{j=1}^l a_j \gamma _j\in \mathbb {Q}(\mu _m, \mathcal {F}^{1/n})$
with
$x=\sum _{j=1}^l a_j \gamma _j\in \mathbb {Q}(\mu _m, \mathcal {F}^{1/n})$
with
![]() $a_j\in \mathbb {Q}(\mu _m, \mathcal {F})$
and
$a_j\in \mathbb {Q}(\mu _m, \mathcal {F})$
and
![]() $\gamma _j\in \langle \mathcal {F}^{1/n}\rangle $
, then
$\gamma _j\in \langle \mathcal {F}^{1/n}\rangle $
, then
![]() $\sigma x = \sum _{j=1}^l \phi _\sigma (a_j)\psi _\sigma (\gamma _j)$
.
$\sigma x = \sum _{j=1}^l \phi _\sigma (a_j)\psi _\sigma (\gamma _j)$
.
The Cartesian product above can be explicitly described. The computation of the left piece can be done thanks to the class field theory and that of the right piece by using a result of Perruca and Sgobba [Reference Perucca and Sgobba19, Theorem 13], see the lemma below.
Lemma 2.1 Let
![]() $L/\mathbb {Q}(\mathcal {F})$
be a finite extension. Then there exists an integer
$L/\mathbb {Q}(\mathcal {F})$
be a finite extension. Then there exists an integer
![]() $C\in \mathbb {N}$
, depending only on
$C\in \mathbb {N}$
, depending only on
![]() $\Gamma $
and L, such that for all
$\Gamma $
and L, such that for all
![]() $d_1,\dots ,d_b\in \mathbb {N}$
divising m, we have
$d_1,\dots ,d_b\in \mathbb {N}$
divising m, we have
 $$\begin{align*}G=\mathrm{Gal}(L(\mu_m, \alpha_1^{1/d_1},\dots, \alpha_b^{1/d_b})/L(\mu_m))\simeq \prod_{l=1}^b \mathbb{Z}/(d_l/c_l)\mathbb{Z}\end{align*}$$
$$\begin{align*}G=\mathrm{Gal}(L(\mu_m, \alpha_1^{1/d_1},\dots, \alpha_b^{1/d_b})/L(\mu_m))\simeq \prod_{l=1}^b \mathbb{Z}/(d_l/c_l)\mathbb{Z}\end{align*}$$
for some positive integers
![]() $c_1,\dots ,c_b\leq C$
.
$c_1,\dots ,c_b\leq C$
.
Proof Put
![]() $L_0= L(\mu _m)$
and
$L_0= L(\mu _m)$
and
![]() $L_l=L_{l-1}(\alpha _l^{1/d_l})$
for all
$L_l=L_{l-1}(\alpha _l^{1/d_l})$
for all
![]() $l\in \{1,\dots ,b\}$
. Let
$l\in \{1,\dots ,b\}$
. Let
![]() $G_l$
denote the Galois group of the extension
$G_l$
denote the Galois group of the extension
![]() $L_l/L_{l-1}$
. Galois theory tells us that G is the inner semidirect product of
$L_l/L_{l-1}$
. Galois theory tells us that G is the inner semidirect product of
![]() $G_b$
and
$G_b$
and
![]() $\mathrm {Gal}(L_{b-1}/L_0)$
. As G is abelian, this product is the Cartesian product. An easy induction shows that
$\mathrm {Gal}(L_{b-1}/L_0)$
. As G is abelian, this product is the Cartesian product. An easy induction shows that
![]() $G\simeq \prod _{l=1}^b G_l$
. For all l, it is trivial that
$G\simeq \prod _{l=1}^b G_l$
. For all l, it is trivial that
![]() $G_l\simeq \mathbb {Z}/(d_l/c_l)\mathbb {Z}$
for some
$G_l\simeq \mathbb {Z}/(d_l/c_l)\mathbb {Z}$
for some
![]() $c_l\in \mathbb {N}$
. So
$c_l\in \mathbb {N}$
. So
![]() $G\simeq \prod _{l=1}^b \mathbb {Z}/(d_l/c_l)\mathbb {Z}$
. Write
$G\simeq \prod _{l=1}^b \mathbb {Z}/(d_l/c_l)\mathbb {Z}$
. Write
![]() $d=\max \{d_1,\dots ,d_b\}$
. Theorem 13 in [Reference Perucca and Sgobba19] claims that the extension
$d=\max \{d_1,\dots ,d_b\}$
. Theorem 13 in [Reference Perucca and Sgobba19] claims that the extension
![]() $L_0(\mathcal {F}^{1/d})/L_0$
has degree at least
$L_0(\mathcal {F}^{1/d})/L_0$
has degree at least
![]() $d^b/C$
for some
$d^b/C$
for some
![]() $C\in \mathbb {N}$
depending only on
$C\in \mathbb {N}$
depending only on
![]() $\Gamma $
and L. On the other hand,
$\Gamma $
and L. On the other hand,
![]() $L_0(\mathcal {F}^{1/d})/L_0(\alpha _1^{1/d_1},\dots , \alpha _b^{1/d_b})$
has degree at most
$L_0(\mathcal {F}^{1/d})/L_0(\alpha _1^{1/d_1},\dots , \alpha _b^{1/d_b})$
has degree at most
![]() $d^b/\prod _{l=1}^b d_l$
. The multiplicativity formula for degrees proves that
$d^b/\prod _{l=1}^b d_l$
. The multiplicativity formula for degrees proves that
![]() $\#G \geq (\prod _{l=1}^b d_l)/C$
; whence
$\#G \geq (\prod _{l=1}^b d_l)/C$
; whence
![]() $\prod _{l=1}^b c_l\leq C$
.
$\prod _{l=1}^b c_l\leq C$
.
Remark 2.2 The isomorphism of Lemma 2.1 is explicit: For each
![]() $(r_1,\dots ,r_b)\in \prod _{l=1}^b \mathbb {Z}/(d_l/c_l)\mathbb {Z}$
, there is an unique
$(r_1,\dots ,r_b)\in \prod _{l=1}^b \mathbb {Z}/(d_l/c_l)\mathbb {Z}$
, there is an unique
![]() $\psi \in G$
such that
$\psi \in G$
such that
![]() $\psi \alpha _l^{1/d_l}=\zeta _{d_l/c_l}^{r_l} \alpha _l^{1/d_l}$
for all l. Moreover, we have
$\psi \alpha _l^{1/d_l}=\zeta _{d_l/c_l}^{r_l} \alpha _l^{1/d_l}$
for all l. Moreover, we have
![]() $\alpha _l^{1/c_l}\in L$
since
$\alpha _l^{1/c_l}\in L$
since
![]() $\psi \alpha _l^{1/c_l}=(\psi \alpha _l^{1/d_l})^{d_l/c_l}=\alpha _l^{1/c_l}$
for all
$\psi \alpha _l^{1/c_l}=(\psi \alpha _l^{1/d_l})^{d_l/c_l}=\alpha _l^{1/c_l}$
for all
![]() $\psi \in G$
. By abuse of notation, this isomorphism becomes from now an equality.
$\psi \in G$
. By abuse of notation, this isomorphism becomes from now an equality.
Remark 2.3 The constant C of Lemma 2.1 can be explicitly determined (see [Reference Perucca and Sgobba19, Remark 20] for details).
3 Proof of Theorem 1.2
It is clear that Conjecture 1.1
![]() $(iii)$
implies the assertion stated in Theorem 1.2. Now, assume that this assertion is true and prove Conjecture 1.1
$(iii)$
implies the assertion stated in Theorem 1.2. Now, assume that this assertion is true and prove Conjecture 1.1
![]() $(iii)$
.
$(iii)$
.
Let
![]() $(x_n)$
be a sequence of
$(x_n)$
be a sequence of
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
$\mathbb {Q}(\Gamma _{\mathrm {div}})^*$
such that
![]() $h(x_n)\to 0$
. We want to show that
$h(x_n)\to 0$
. We want to show that
![]() $x_n\in \Gamma _{\mathrm {div}}$
for all n large enough. For this, assume by contradiction that
$x_n\in \Gamma _{\mathrm {div}}$
for all n large enough. For this, assume by contradiction that
![]() $x_n\notin \Gamma _{\mathrm {div}}$
for infinitely many n, that is for all n by taking a suitable subsequence.
$x_n\notin \Gamma _{\mathrm {div}}$
for infinitely many n, that is for all n by taking a suitable subsequence.
Lemma 3.1 We have
![]() $[\mathbb {Q}(x_n^2) : \mathbb {Q}]\to +\infty $
.
$[\mathbb {Q}(x_n^2) : \mathbb {Q}]\to +\infty $
.
Proof Let l be an accumulation point of the sequence
![]() $([\mathbb {Q}(x_n^2) : \mathbb {Q}])$
. Passing to a subsequence, we get
$([\mathbb {Q}(x_n^2) : \mathbb {Q}])$
. Passing to a subsequence, we get
![]() $[\mathbb {Q}(x_n^2) : \mathbb {Q}]\to l$
. If
$[\mathbb {Q}(x_n^2) : \mathbb {Q}]\to l$
. If
![]() $l<+\infty $
, then our sequence is bounded and Northcott’s theorem implies that
$l<+\infty $
, then our sequence is bounded and Northcott’s theorem implies that
![]() $x_n^2\in \mu _\infty \subset \Gamma _{\mathrm {div}}$
for all n large enough, which is absurd. So
$x_n^2\in \mu _\infty \subset \Gamma _{\mathrm {div}}$
for all n large enough, which is absurd. So
![]() $l=+\infty $
and the lemma follows.
$l=+\infty $
and the lemma follows.
Recall that
![]() $K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )=\mathbb {Q}(\mu _\infty , \mathcal {F})$
and note that
$K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )=\mathbb {Q}(\mu _\infty , \mathcal {F})$
and note that
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})=\bigcup _{n\in \mathbb {N}} K_\Gamma (\mathcal {F}^{1/n})$
.
$\mathbb {Q}(\Gamma _{\mathrm {div}})=\bigcup _{n\in \mathbb {N}} K_\Gamma (\mathcal {F}^{1/n})$
.
Lemma 3.2 There is a sequence
![]() $(\sigma _n)$
of
$(\sigma _n)$
of
![]() $\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q}(\mathcal {F}))$
such that
$\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q}(\mathcal {F}))$
such that
![]() $d_{\Gamma , \varepsilon }(\sigma _n x_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma , \varepsilon }(\sigma _n x_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Proof Let
![]() $n\in \mathbb {N}$
. There exists
$n\in \mathbb {N}$
. There exists
![]() $m_n\in \mathbb {N}$
such that
$m_n\in \mathbb {N}$
such that
![]() $x_n\in K_\Gamma (\mathcal {F}^{1/m_n})$
. We can also find a multiple
$x_n\in K_\Gamma (\mathcal {F}^{1/m_n})$
. We can also find a multiple
![]() $m^{\prime }_n\in \mathbb {N}$
of
$m^{\prime }_n\in \mathbb {N}$
of
![]() $m_n$
such that:
$m_n$
such that:
-
(i)
 $x_n\in \mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}^{1/m_n})$
.
$x_n\in \mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}^{1/m_n})$
. -
(ii) The restriction map
 $\mathrm {Gal}(K_\Gamma (\mathcal {F}^{1/m_n})/K_\Gamma )\to H_n=\mathrm {Gal}(\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}^{1/m_n})/\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}))$
is an isomorphism.
$\mathrm {Gal}(K_\Gamma (\mathcal {F}^{1/m_n})/K_\Gamma )\to H_n=\mathrm {Gal}(\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}^{1/m_n})/\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}))$
is an isomorphism.
Express
![]() $x_n$
as
$x_n$
as
![]() $x_n=\sum _{j=1}^{l_n} a_{j,n}\gamma _{j,n}$
with
$x_n=\sum _{j=1}^{l_n} a_{j,n}\gamma _{j,n}$
with
![]() $a_{j,n}\in \mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F})$
and
$a_{j,n}\in \mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F})$
and
![]() $\gamma _{j,n}\in \langle \mathcal {F}^{1/m_n}\rangle $
. Fix
$\gamma _{j,n}\in \langle \mathcal {F}^{1/m_n}\rangle $
. Fix
![]() $\varepsilon>0$
. For any
$\varepsilon>0$
. For any
![]() $\phi \in N_n=\mathrm {Gal}(\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F})/\mathbb {Q}(\mathcal {F}))$
, we set
$\phi \in N_n=\mathrm {Gal}(\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F})/\mathbb {Q}(\mathcal {F}))$
, we set
 $$\begin{align*}d_{n}(\phi)=\frac{\#\left\{\psi\in H_n, 1-\varepsilon \leq \left\vert \sum_{j=1}^{l_n} \phi(a_{j,n})\psi(\gamma_{j,n})\right\vert{}^2\leq 1+\varepsilon \right\}}{\# H_n} \end{align*}$$
$$\begin{align*}d_{n}(\phi)=\frac{\#\left\{\psi\in H_n, 1-\varepsilon \leq \left\vert \sum_{j=1}^{l_n} \phi(a_{j,n})\psi(\gamma_{j,n})\right\vert{}^2\leq 1+\varepsilon \right\}}{\# H_n} \end{align*}$$
and we pick
![]() $\phi _n\in N_n$
such that
$\phi _n\in N_n$
such that
![]() $d_n(\phi _n)=\max _{\phi \in N_n} \{d_n(\phi )\}$
.
$d_n(\phi _n)=\max _{\phi \in N_n} \{d_n(\phi )\}$
.
By Galois theory,
![]() $G_n=\mathrm {Gal}(\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}^{1/m_n})/\mathbb {Q}(\mathcal {F}))$
is isomorphic to the inner semidirect product of
$G_n=\mathrm {Gal}(\mathbb {Q}(\zeta _{m^{\prime }_n}, \mathcal {F}^{1/m_n})/\mathbb {Q}(\mathcal {F}))$
is isomorphic to the inner semidirect product of
![]() $N_n$
and
$N_n$
and
![]() $H_n$
. Denote by
$H_n$
. Denote by
![]() $\sigma _n$
the element of
$\sigma _n$
the element of
![]() $G_n$
corresponding to the pair
$G_n$
corresponding to the pair
![]() $(\phi _n, 1)\in N_n\times H_n$
. Section 2 tells us that
$(\phi _n, 1)\in N_n\times H_n$
. Section 2 tells us that
![]() $\sigma _n x_n = \sum _{j=1}^{l_n} \phi _n(a_{j,n})\gamma _{j,n}$
.
$\sigma _n x_n = \sum _{j=1}^{l_n} \phi _n(a_{j,n})\gamma _{j,n}$
.
From (i) and (ii), we infer that
![]() $O_\Gamma (\sigma _n x_n)$
is equal to the orbit of
$O_\Gamma (\sigma _n x_n)$
is equal to the orbit of
![]() $\sigma _n x_n$
under
$\sigma _n x_n$
under
![]() $H_n$
. Thus, it follows from the definition of
$H_n$
. Thus, it follows from the definition of
![]() $d_{\Gamma ,\varepsilon }(\sigma _n x_n)$
(see Section 1.2) that
$d_{\Gamma ,\varepsilon }(\sigma _n x_n)$
(see Section 1.2) that
 $$\begin{align*}d_{\Gamma, \varepsilon}(\sigma_n x_n) = \frac{\#\{\psi \in H_n, 1-\varepsilon\leq \vert \psi\sigma_n x_n\vert^2\leq 1+\varepsilon\}}{\#H_n} = d_n(\phi_n). \end{align*}$$
$$\begin{align*}d_{\Gamma, \varepsilon}(\sigma_n x_n) = \frac{\#\{\psi \in H_n, 1-\varepsilon\leq \vert \psi\sigma_n x_n\vert^2\leq 1+\varepsilon\}}{\#H_n} = d_n(\phi_n). \end{align*}$$
A small calculation gives
 $$\begin{align*}\begin{aligned} u_n &= \#\{\sigma\in G_n, 1-\varepsilon\leq \vert \sigma x_n\vert^2\leq 1+\varepsilon \} \\ &= \#\left\{(\phi,\psi)\in N_n\times H_n, 1-\varepsilon\leq \left\vert \sum_{j=1}^{l_n} \phi(a_{j,n})\psi(\gamma_{j,n})\right\vert{}^2\leq 1+\varepsilon\right\} \\ &= \sum_{\phi\in N_n} \#\left\{\psi \in H_n, 1-\varepsilon\leq \left\vert \sum_{j=1}^{l_n} \phi(a_{j,n})\psi(\gamma_{j,n})\right\vert{}^2\leq 1+\varepsilon\right\}, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} u_n &= \#\{\sigma\in G_n, 1-\varepsilon\leq \vert \sigma x_n\vert^2\leq 1+\varepsilon \} \\ &= \#\left\{(\phi,\psi)\in N_n\times H_n, 1-\varepsilon\leq \left\vert \sum_{j=1}^{l_n} \phi(a_{j,n})\psi(\gamma_{j,n})\right\vert{}^2\leq 1+\varepsilon\right\} \\ &= \sum_{\phi\in N_n} \#\left\{\psi \in H_n, 1-\varepsilon\leq \left\vert \sum_{j=1}^{l_n} \phi(a_{j,n})\psi(\gamma_{j,n})\right\vert{}^2\leq 1+\varepsilon\right\}, \end{aligned}\end{align*}$$
and so
 $$ \begin{align} \frac{u_n}{\#G_n} = \frac{1}{\#N_n}\sum_{\phi\in N_n} d_n(\phi) \leq d_n(\phi_n)= d_{\Gamma,\varepsilon}(\sigma_n x_n)\leq 1. \end{align} $$
$$ \begin{align} \frac{u_n}{\#G_n} = \frac{1}{\#N_n}\sum_{\phi\in N_n} d_n(\phi) \leq d_n(\phi_n)= d_{\Gamma,\varepsilon}(\sigma_n x_n)\leq 1. \end{align} $$
Recall that
![]() $\mathcal {F}$
is a finite set. As
$\mathcal {F}$
is a finite set. As
![]() $h(x_n^2)=2h(x_n)\to 0$
and
$h(x_n^2)=2h(x_n)\to 0$
and
![]() $[\mathbb {Q}(\mathcal {F}, x_n^2) :\mathbb {Q}(\mathcal {F})]= [\mathbb {Q}(\mathcal {F}, x_n^2) : \mathbb {Q}]/[\mathbb {Q}(\mathcal {F}):\mathbb {Q}]\to +\infty $
by Lemma 3.1, we infer from Bilu’s equidistribution theorem [Reference Yuan30, Subsection 1.1, Theorem] applied to
$[\mathbb {Q}(\mathcal {F}, x_n^2) :\mathbb {Q}(\mathcal {F})]= [\mathbb {Q}(\mathcal {F}, x_n^2) : \mathbb {Q}]/[\mathbb {Q}(\mathcal {F}):\mathbb {Q}]\to +\infty $
by Lemma 3.1, we infer from Bilu’s equidistribution theorem [Reference Yuan30, Subsection 1.1, Theorem] applied to
![]() $K=\mathbb {Q}(\mathcal {F})$
that
$K=\mathbb {Q}(\mathcal {F})$
that
![]() $u_n/\#G_n$
goes to
$u_n/\#G_n$
goes to
![]() $1$
as
$1$
as
![]() $n\to +\infty $
. Lemma follows by involving the squeeze theorem in (1).
$n\to +\infty $
. Lemma follows by involving the squeeze theorem in (1).
Proof of Theorem 1.4
We have
![]() $h(\sigma _n x_n)=h(x_n)\to 0$
and
$h(\sigma _n x_n)=h(x_n)\to 0$
and
![]() $d_{\Gamma , \varepsilon }(\sigma _n x_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma , \varepsilon }(\sigma _n x_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
by Lemma 3.2. Applying the assertion of Theorem 1.2 (which is assumed to be true) to
$\varepsilon>0$
by Lemma 3.2. Applying the assertion of Theorem 1.2 (which is assumed to be true) to
![]() $y_n=\sigma _n x_n$
shows that
$y_n=\sigma _n x_n$
shows that
![]() $\sigma _n x_n\in \Gamma _{\mathrm {div}}$
for all n large enough.
$\sigma _n x_n\in \Gamma _{\mathrm {div}}$
for all n large enough.
By definition of the division group, we deduce that
![]() $\sigma _n (x_n^{j_n})\in \langle \mathcal {F}\rangle $
for some integer
$\sigma _n (x_n^{j_n})\in \langle \mathcal {F}\rangle $
for some integer
![]() $j_n\in \mathbb {N}$
. As
$j_n\in \mathbb {N}$
. As
![]() $\sigma _n$
fixes the elements of
$\sigma _n$
fixes the elements of
![]() $\mathcal {F}$
, we conclude
$\mathcal {F}$
, we conclude
![]() $x_n^{j_n}\in \langle \mathcal {F} \rangle \subset \Gamma $
, which contradicts the fact that
$x_n^{j_n}\in \langle \mathcal {F} \rangle \subset \Gamma $
, which contradicts the fact that
![]() $x_n\notin \Gamma _{\mathrm {div}}$
. This finishes the proof of Theorem 1.2.
$x_n\notin \Gamma _{\mathrm {div}}$
. This finishes the proof of Theorem 1.2.
4 Direct image of
 $\mu _d$
under a meromorphic function
$\mu _d$
under a meromorphic function
Definition 4.1 Let
![]() $N\in \mathbb {N}$
. Denote by
$N\in \mathbb {N}$
. Denote by
![]() $\mathcal {S}_N$
the set of integers
$\mathcal {S}_N$
the set of integers
![]() $d\in \mathbb {N}$
for which there exists a meromorphic function
$d\in \mathbb {N}$
for which there exists a meromorphic function
![]() $f(z)= \sum _{j=1}^N a_j z^{b_j}$
on
$f(z)= \sum _{j=1}^N a_j z^{b_j}$
on
![]() $\mathbb {C}^*$
satisfying
$\mathbb {C}^*$
satisfying
![]() $\vert f(\zeta ) \vert =1$
for all
$\vert f(\zeta ) \vert =1$
for all
![]() $\zeta \in \mu _d$
. Moreover, we impose that:
$\zeta \in \mu _d$
. Moreover, we impose that:
-
•
 $b_1=0,b_2, \dots ,b_N\in \mathbb {Z}$
are pairwise distinct integers such that
$b_1=0,b_2, \dots ,b_N\in \mathbb {Z}$
are pairwise distinct integers such that
 $b_1,\dots ,b_N$
and d have no common positive factors other than
$b_1,\dots ,b_N$
and d have no common positive factors other than
 $1$
;
$1$
; -
•
 $a_1,\dots ,a_N\in \mathbb {C}$
satisfy
$a_1,\dots ,a_N\in \mathbb {C}$
satisfy
 $\sum _{i\in I} a_i\neq 0$
for all non-empty subsets
$\sum _{i\in I} a_i\neq 0$
for all non-empty subsets
 $I\subset \{1,\dots , N\}$
.
$I\subset \{1,\dots , N\}$
.
The study of
![]() $\mathcal {S}_N$
might be of independent interest, but we only prove in this section what is needed for this article, namely the finiteness of it for all
$\mathcal {S}_N$
might be of independent interest, but we only prove in this section what is needed for this article, namely the finiteness of it for all
![]() $N\in \mathbb {N}$
.
$N\in \mathbb {N}$
.
Let
![]() $N\geq 2$
, and let
$N\geq 2$
, and let
![]() $d\in \mathcal {S}_N$
be greater than
$d\in \mathcal {S}_N$
be greater than
![]() $4^N (N^2-1)$
. The lemma below asserts that regardless of the choice of integers
$4^N (N^2-1)$
. The lemma below asserts that regardless of the choice of integers
![]() $b_1,\dots ,b_N$
as in Definition 4.1, at least one of them has an absolute value greater than or equal to
$b_1,\dots ,b_N$
as in Definition 4.1, at least one of them has an absolute value greater than or equal to
![]() $d/4$
. We will then contradict this claim thanks to Dirichlet’s theorem on simultaneous approximation.
$d/4$
. We will then contradict this claim thanks to Dirichlet’s theorem on simultaneous approximation.
Lemma 4.2 Let
![]() $M\geq 2$
, and let
$M\geq 2$
, and let
![]() $g(z)=\sum _{j=1}^M u_j z^{c_j}$
be a meromorphic function on
$g(z)=\sum _{j=1}^M u_j z^{c_j}$
be a meromorphic function on
![]() $\mathbb {C}^*$
with
$\mathbb {C}^*$
with
![]() $u_1,\dots ,u_M\in \mathbb {C}^*$
and
$u_1,\dots ,u_M\in \mathbb {C}^*$
and
![]() $c_1,\dots ,c_M\in \mathbb {Z}$
pairwise distinct integers. If
$c_1,\dots ,c_M\in \mathbb {Z}$
pairwise distinct integers. If
![]() $d\geq M^2$
is an integer such that
$d\geq M^2$
is an integer such that
![]() $\vert g(\zeta )\vert =1$
for all
$\vert g(\zeta )\vert =1$
for all
![]() $\zeta \in \mu _d$
, then
$\zeta \in \mu _d$
, then
![]() $\max \{\vert c_1\vert ,\dots , \vert c_M\vert \} \geq d/4$
.
$\max \{\vert c_1\vert ,\dots , \vert c_M\vert \} \geq d/4$
.
Proof Assume by contradiction that
![]() $\max \{\vert c_1\vert ,\dots , \vert c_M\vert \} < d/4$
. Write
$\max \{\vert c_1\vert ,\dots , \vert c_M\vert \} < d/4$
. Write
with
![]() $n\leq M^2$
and
$n\leq M^2$
and
![]() $\gamma _1,\dots , \gamma _n$
pairwise distinct. Note that
$\gamma _1,\dots , \gamma _n$
pairwise distinct. Note that
![]() $0=c_1-c_1\in \{\gamma _1,\dots ,\gamma _n\}$
. We can thus assume that
$0=c_1-c_1\in \{\gamma _1,\dots ,\gamma _n\}$
. We can thus assume that
![]() $\gamma _1=0$
. Moreover,
$\gamma _1=0$
. Moreover,
![]() $\gamma _k\in [-d/2, d/2]$
for all k since
$\gamma _k\in [-d/2, d/2]$
for all k since
![]() $\max \{\vert c_1\vert ,\dots , \vert c_M\vert \} < d/4$
.
$\max \{\vert c_1\vert ,\dots , \vert c_M\vert \} < d/4$
.
For each
![]() $k\in \{1,\dots ,n\}$
, define
$k\in \{1,\dots ,n\}$
, define
![]() $E_k$
as the set of pairs
$E_k$
as the set of pairs
![]() $(i,j)\in \{1,\dots , M\}^2$
for which
$(i,j)\in \{1,\dots , M\}^2$
for which
![]() $\gamma _k=c_i-c_j$
. Clearly,
$\gamma _k=c_i-c_j$
. Clearly,
![]() $E_1,\dots , E_n$
is a partition of
$E_1,\dots , E_n$
is a partition of
![]() $\{1,\dots ,M\}^2$
. Then put
$\{1,\dots ,M\}^2$
. Then put
![]() $v_k= \sum _{(i,j)\in E_k} u_i\overline {u_j}$
. An easy calculation gives, for all
$v_k= \sum _{(i,j)\in E_k} u_i\overline {u_j}$
. An easy calculation gives, for all
![]() $l\in \{0,\dots ,d-1\}$
,
$l\in \{0,\dots ,d-1\}$
,
 $$ \begin{align} \begin{aligned} \sum_{k=1}^n \zeta_d^{l\gamma_k} v_k & = \sum_{k=1}^n \sum_{(i,j)\in E_k}u_i\overline{u_j} \zeta_d^{l(c_i-c_j)} \\ & = \sum_{(i,j)\in \bigsqcup_{k=1}^n E_k} u_i\overline{u_j} \zeta_d^{l(c_i-c_j)} = \sum_{1\leq i,j\leq M} u_i\overline{u_j} \zeta_d^{l(c_i-c_j)} \\ & = \left(\sum_{i=1}^M u_i \zeta_d^{lc_i}\right) \left(\sum_{j=1}^M \overline{u_j} \zeta_d^{-l c_j}\right) = g(\zeta_d^l)\overline{g(\zeta_d^l)}= 1, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{k=1}^n \zeta_d^{l\gamma_k} v_k & = \sum_{k=1}^n \sum_{(i,j)\in E_k}u_i\overline{u_j} \zeta_d^{l(c_i-c_j)} \\ & = \sum_{(i,j)\in \bigsqcup_{k=1}^n E_k} u_i\overline{u_j} \zeta_d^{l(c_i-c_j)} = \sum_{1\leq i,j\leq M} u_i\overline{u_j} \zeta_d^{l(c_i-c_j)} \\ & = \left(\sum_{i=1}^M u_i \zeta_d^{lc_i}\right) \left(\sum_{j=1}^M \overline{u_j} \zeta_d^{-l c_j}\right) = g(\zeta_d^l)\overline{g(\zeta_d^l)}= 1, \end{aligned} \end{align} $$
the last equality coming from the fact that
![]() $\vert g(\zeta )\vert =1$
for all
$\vert g(\zeta )\vert =1$
for all
![]() $\zeta \in \mu _d$
. We recognize a linear system with n unknowns (namely,
$\zeta \in \mu _d$
. We recognize a linear system with n unknowns (namely,
![]() $v_1,\dots ,v_n$
) and d equations. By assumption,
$v_1,\dots ,v_n$
) and d equations. By assumption,
![]() $d\geq M^2\geq n$
. The (square) matrix associated with the linear subsystem
$d\geq M^2\geq n$
. The (square) matrix associated with the linear subsystem
 $$ \begin{align} \forall l\in\{0,\dots,n-1\}, \; \; \; \; \; \sum_{k=1}^n \zeta_d^{l\gamma_k} v_k = 1 \end{align} $$
$$ \begin{align} \forall l\in\{0,\dots,n-1\}, \; \; \; \; \; \sum_{k=1}^n \zeta_d^{l\gamma_k} v_k = 1 \end{align} $$
is the Vandermonde matrix
![]() $\left (\zeta _d^{l \gamma _k}\right )_{\underset {1\leq k \leq n}{0\leq l\leq n-1}}$
. It is well-known that its determinant is
$\left (\zeta _d^{l \gamma _k}\right )_{\underset {1\leq k \leq n}{0\leq l\leq n-1}}$
. It is well-known that its determinant is
![]() $\prod _{1\leq i<j \leq n} (\zeta _d^{\gamma _j}-\zeta _d^{\gamma _i})$
. As
$\prod _{1\leq i<j \leq n} (\zeta _d^{\gamma _j}-\zeta _d^{\gamma _i})$
. As
![]() $\gamma _1,\dots ,\gamma _n\in [-d/2, d/2]$
are pairwise distinct, the numbers
$\gamma _1,\dots ,\gamma _n\in [-d/2, d/2]$
are pairwise distinct, the numbers
![]() $\zeta _d^{\gamma _1},\dots , \zeta _d^{\gamma _n}$
are therefore pairwise distinct. Hence, the determinant above is nonzero, and so (3) has a unique solution. Thus, (2) has at most one solution. As
$\zeta _d^{\gamma _1},\dots , \zeta _d^{\gamma _n}$
are therefore pairwise distinct. Hence, the determinant above is nonzero, and so (3) has a unique solution. Thus, (2) has at most one solution. As
![]() $\gamma _1=0$
, it follows that
$\gamma _1=0$
, it follows that
![]() $(v_1,\dots ,v_n)=(1,0,\dots ,0)$
is the unique solution of (2).
$(v_1,\dots ,v_n)=(1,0,\dots ,0)$
is the unique solution of (2).
Denote by
![]() $i_0$
, resp.
$i_0$
, resp.
![]() $j_0$
, the element of
$j_0$
, the element of
![]() $\{1,\dots , M\}$
such that
$\{1,\dots , M\}$
such that
Let
![]() $m\in \{1,\dots ,n\}$
be the integer such that
$m\in \{1,\dots ,n\}$
be the integer such that
![]() $\gamma _m=c_{i_0}-c_{j_0}$
, and let
$\gamma _m=c_{i_0}-c_{j_0}$
, and let
![]() $(i,j)\in E_m$
. Then
$(i,j)\in E_m$
. Then
![]() $c_i-c_j=c_{i_0}-c_{j_0}$
and (4) leads to
$c_i-c_j=c_{i_0}-c_{j_0}$
and (4) leads to
![]() $c_i=c_{i_0}$
and
$c_i=c_{i_0}$
and
![]() $c_j=c_{j_0}$
. As
$c_j=c_{j_0}$
. As
![]() $c_1,\dots ,c_M$
are pairwise distinct, we get
$c_1,\dots ,c_M$
are pairwise distinct, we get
![]() $(i,j)=(i_0,j_0)$
. In conclusion,
$(i,j)=(i_0,j_0)$
. In conclusion,
![]() $E_m=\{(i_0, j_0)\}$
.
$E_m=\{(i_0, j_0)\}$
.
Recall that
![]() $\gamma _1=0$
. So the set
$\gamma _1=0$
. So the set
![]() $E_1$
contains at least
$E_1$
contains at least
![]() $M\geq 2$
elements, namely,
$M\geq 2$
elements, namely,
![]() $(1,1),\dots ,(M,M)$
; whence
$(1,1),\dots ,(M,M)$
; whence
![]() $m>1$
. But then, by the foregoing, we have
$m>1$
. But then, by the foregoing, we have
i.e., either
![]() $u_{i_0}=0$
or
$u_{i_0}=0$
or
![]() $u_{j_0}=0$
, which is absurd. This completes the proof.
$u_{j_0}=0$
, which is absurd. This completes the proof.
We can now prove the desired result.
Theorem 4.3 For all
![]() $N\in \mathbb {N}$
, the set
$N\in \mathbb {N}$
, the set
![]() $\mathcal {S}_N$
is finite. Moreover,
$\mathcal {S}_N$
is finite. Moreover,
![]() $\mathcal {S}_1=\{1\}$
and
$\mathcal {S}_1=\{1\}$
and
![]() $4^N (N^2-1)$
is an upper bound of
$4^N (N^2-1)$
is an upper bound of
![]() $\mathcal {S}_N$
for all
$\mathcal {S}_N$
for all
![]() $N\geq 2$
.
$N\geq 2$
.
Proof Let
![]() $d\in \mathcal {S}_N$
. There is a meromorphic function
$d\in \mathcal {S}_N$
. There is a meromorphic function
![]() $f(z)= \sum _{j=1}^N a_jz^{b_j}$
on
$f(z)= \sum _{j=1}^N a_jz^{b_j}$
on
![]() $\mathbb {C}^*$
such that
$\mathbb {C}^*$
such that
![]() $\vert f(\zeta )\vert =1$
for all
$\vert f(\zeta )\vert =1$
for all
![]() $\zeta \in \mu _d$
, where
$\zeta \in \mu _d$
, where
![]() $a_1,\dots , a_N$
and
$a_1,\dots , a_N$
and
![]() $b_1,\dots , b_N$
are as in Definition 4.1. If
$b_1,\dots , b_N$
are as in Definition 4.1. If
![]() $N=1$
, then d has to be coprime to
$N=1$
, then d has to be coprime to
![]() $b_1=0$
, i.e.,
$b_1=0$
, i.e.,
![]() $d=1$
. As
$d=1$
. As
![]() $\vert 1\vert =1$
, we get
$\vert 1\vert =1$
, we get
![]() $\mathcal {S}_1=\{1\}$
. Now assume that
$\mathcal {S}_1=\{1\}$
. Now assume that
![]() $N\geq 2$
.
$N\geq 2$
.
Dirichlet’s theorem on simultaneous approximation asserts the existence of integers
![]() $p_1,\dots ,p_N\in \mathbb {Z}$
and
$p_1,\dots ,p_N\in \mathbb {Z}$
and
![]() $q\in \{1,\dots ,4^N\}$
such that
$q\in \{1,\dots ,4^N\}$
such that
![]() $\vert q (b_j/d) - p_j\vert < 1/4$
for all
$\vert q (b_j/d) - p_j\vert < 1/4$
for all
![]() $j\in \{1,\dots ,N\}$
. Write e for the greatest common divisor of q and d, then put
$j\in \{1,\dots ,N\}$
. Write e for the greatest common divisor of q and d, then put
![]() $q'=q/e$
and
$q'=q/e$
and
![]() $d'=d/e$
. Clearly,
$d'=d/e$
. Clearly,
![]() $q'$
and
$q'$
and
![]() $d'$
are coprime,
$d'$
are coprime,
![]() $e\in \{1,\dots ,4^N\}$
and
$e\in \{1,\dots ,4^N\}$
and
Put
![]() $\{c_1,\dots ,c_M\}=\{q'b_1-d'p_1, \dots , q'b_N-d'p_N\}$
, where
$\{c_1,\dots ,c_M\}=\{q'b_1-d'p_1, \dots , q'b_N-d'p_N\}$
, where
![]() $c_1,\dots ,c_M$
are pairwise distinct. We can assume that
$c_1,\dots ,c_M$
are pairwise distinct. We can assume that
![]() $c_1=q'b_1-d'p_1$
. For all
$c_1=q'b_1-d'p_1$
. For all
![]() $k\in \{1,\dots , M\}$
, denote by
$k\in \{1,\dots , M\}$
, denote by
![]() $E_k$
the set of integers
$E_k$
the set of integers
![]() $j\in \{1,\dots ,N\}$
such that
$j\in \{1,\dots ,N\}$
such that
![]() $c_k=q'b_j-d'p_j$
. Clearly
$c_k=q'b_j-d'p_j$
. Clearly
![]() $E_1,\dots , E_M$
is a partition of
$E_1,\dots , E_M$
is a partition of
![]() $\{1,\dots ,N\}$
. Put
$\{1,\dots ,N\}$
. Put
![]() $u_k=\sum _{j\in E_k} a_j$
and
$u_k=\sum _{j\in E_k} a_j$
and
![]() $g(z)=\sum _{k=1}^M u_k z^{c_k}$
.
$g(z)=\sum _{k=1}^M u_k z^{c_k}$
.
As
![]() $b_1=0$
by Definition 4.1 and
$b_1=0$
by Definition 4.1 and
![]() $\vert p_1\vert <1/4$
by (5), we conclude
$\vert p_1\vert <1/4$
by (5), we conclude
![]() $c_1=0$
. Let n be a common positive factor of
$c_1=0$
. Let n be a common positive factor of
![]() $c_1,\dots ,c_M$
and
$c_1,\dots ,c_M$
and
![]() $d'$
. From the definition of
$d'$
. From the definition of
![]() $c_i$
, we deduce that n divides
$c_i$
, we deduce that n divides
![]() $q'b_1,\dots ,q'b_N$
and
$q'b_1,\dots ,q'b_N$
and
![]() $q'd'$
. By Definition 4.1,
$q'd'$
. By Definition 4.1,
![]() $b_1,\dots ,b_N$
and
$b_1,\dots ,b_N$
and
![]() $d'$
have no common positive factors other than
$d'$
have no common positive factors other than
![]() $1$
since
$1$
since
![]() $d'$
divides d. Hence, n divides
$d'$
divides d. Hence, n divides
![]() $q'$
. But it divides
$q'$
. But it divides
![]() $d'$
too. Whence
$d'$
too. Whence
![]() $n=1$
since
$n=1$
since
![]() $q'$
and
$q'$
and
![]() $d'$
are coprime.
$d'$
are coprime.
We have
![]() $\sum _{k\in I} u_k \neq 0$
for all non-empty subsets
$\sum _{k\in I} u_k \neq 0$
for all non-empty subsets
![]() $I\subset \{1,\dots , M\}$
since otherwise,
$I\subset \{1,\dots , M\}$
since otherwise,
which disagrees with Definition 4.1. In particular,
![]() $u_1,\dots ,u_M\in \mathbb {C}^*$
. Finally,
$u_1,\dots ,u_M\in \mathbb {C}^*$
. Finally,
 $$ \begin{align*} \forall l\in\mathbb{Z}, \; \; \; \; \; f(\zeta_d^{ql}) & = \sum_{j=1}^N a_j\zeta_d^{q b_j l} = \sum_{j=1}^N a_j\zeta_{d'}^{q'b_j l} = \sum_{j=1}^N a_j\zeta_{d'}^{(q'b_j-d'p_j)l} \\ & = \sum_{k=1}^M\sum_{j\in E_k} a_j\zeta_{d'}^{(q'b_j-d'p_j)l} = \sum_{k=1}^M u_k \zeta_{d'}^{c_kl} = g(\zeta_{d'}^l). \end{align*} $$
$$ \begin{align*} \forall l\in\mathbb{Z}, \; \; \; \; \; f(\zeta_d^{ql}) & = \sum_{j=1}^N a_j\zeta_d^{q b_j l} = \sum_{j=1}^N a_j\zeta_{d'}^{q'b_j l} = \sum_{j=1}^N a_j\zeta_{d'}^{(q'b_j-d'p_j)l} \\ & = \sum_{k=1}^M\sum_{j\in E_k} a_j\zeta_{d'}^{(q'b_j-d'p_j)l} = \sum_{k=1}^M u_k \zeta_{d'}^{c_kl} = g(\zeta_{d'}^l). \end{align*} $$
As
![]() $\vert f(\zeta )\vert =1$
for all
$\vert f(\zeta )\vert =1$
for all
![]() $\zeta \in \mu _d$
, we infer that
$\zeta \in \mu _d$
, we infer that
![]() $\vert g(\zeta )\vert =1$
for all
$\vert g(\zeta )\vert =1$
for all
![]() $\zeta \in \mu _{d'}$
.
$\zeta \in \mu _{d'}$
.
Of all this, we conclude
![]() $d'\in \mathcal {S}_M$
. Recall that
$d'\in \mathcal {S}_M$
. Recall that
![]() $d'=d/e$
with
$d'=d/e$
with
![]() $e\in \{1,\dots , 4^N\}$
, that
$e\in \{1,\dots , 4^N\}$
, that
![]() $u_1,\dots ,u_M\in \mathbb {C}^*$
, that
$u_1,\dots ,u_M\in \mathbb {C}^*$
, that
![]() $c_1,\dots ,c_M\in \mathbb {Z}$
are pairwise distinct, that
$c_1,\dots ,c_M\in \mathbb {Z}$
are pairwise distinct, that
![]() $\vert g(\zeta )\vert =1$
for all
$\vert g(\zeta )\vert =1$
for all
![]() $\zeta \in \mu _{d'}$
and that
$\zeta \in \mu _{d'}$
and that
![]() $\max \{\vert c_1\vert , \dots , \vert c_M\vert \}<d'/4$
by (5). If
$\max \{\vert c_1\vert , \dots , \vert c_M\vert \}<d'/4$
by (5). If
![]() $M\geq 2$
, then Lemma 4.2 applied to
$M\geq 2$
, then Lemma 4.2 applied to
![]() $d=d'$
implies
$d=d'$
implies
![]() $d'=d/e < M^2$
; whence
$d'=d/e < M^2$
; whence
![]() $d \leq 4^N (N^2-1)$
. If
$d \leq 4^N (N^2-1)$
. If
![]() $M=1$
, then
$M=1$
, then
![]() $d'=1$
since
$d'=1$
since
![]() $\mathcal {S}_1=\{1\}$
. Thus,
$\mathcal {S}_1=\{1\}$
. Thus,
![]() $d\leq 4^N$
and the theorem follows.
$d\leq 4^N$
and the theorem follows.
5 Proof of Theorem 1.9
Fix once and for all an integer
![]() $N\in \mathbb {N}$
. Recall that the length of an element
$N\in \mathbb {N}$
. Recall that the length of an element
![]() $y\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
is defined to be the smallest
$y\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
is defined to be the smallest
![]() $l\in \mathbb {N}$
for which y can express as
$l\in \mathbb {N}$
for which y can express as
![]() $y=\sum _{j=1}^l y_j \gamma _j$
with
$y=\sum _{j=1}^l y_j \gamma _j$
with
![]() $y_j\in K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )$
and
$y_j\in K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )$
and
![]() $\gamma _j\in \Gamma _{\mathrm {div}}$
. The lemma below shows that the length is invariant under translation of points in
$\gamma _j\in \Gamma _{\mathrm {div}}$
. The lemma below shows that the length is invariant under translation of points in
![]() $\Gamma _{\mathrm {div}}$
.
$\Gamma _{\mathrm {div}}$
.
Lemma 5.1 Let
![]() $y\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
, and let
$y\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
, and let
![]() $z\in \Gamma _{\mathrm {div}}$
. Then y and
$z\in \Gamma _{\mathrm {div}}$
. Then y and
![]() $yz$
have the same length.
$yz$
have the same length.
Proof Denote by l, resp.
![]() $l'$
, the length of y, resp.
$l'$
, the length of y, resp.
![]() $yz$
. We can express y as
$yz$
. We can express y as
![]() $y=\sum _{j=1}^l y_j \gamma _j$
with
$y=\sum _{j=1}^l y_j \gamma _j$
with
![]() $y_j\in K_\Gamma $
and
$y_j\in K_\Gamma $
and
![]() $\gamma _j\in \Gamma _{\mathrm {div}}$
. Hence,
$\gamma _j\in \Gamma _{\mathrm {div}}$
. Hence,
![]() $yz=\sum _{j=1}^l y_j (\gamma _j z)$
and the definition of the length leads to
$yz=\sum _{j=1}^l y_j (\gamma _j z)$
and the definition of the length leads to
![]() $l'\leq l$
. The inequality
$l'\leq l$
. The inequality
![]() $l\leq l'$
is obtained by replacing y with
$l\leq l'$
is obtained by replacing y with
![]() $yz$
and z with
$yz$
and z with
![]() $z^{-1}\in \Gamma _{\mathrm {div}}$
. This completes the proof.
$z^{-1}\in \Gamma _{\mathrm {div}}$
. This completes the proof.
Recall that
![]() $\mathcal {F}=\{\alpha _1,\dots ,\alpha _b\}$
is the torsion-free part of
$\mathcal {F}=\{\alpha _1,\dots ,\alpha _b\}$
is the torsion-free part of
![]() $\Gamma $
and that
$\Gamma $
and that
![]() $l_N(\Gamma )$
denotes the set of elements in
$l_N(\Gamma )$
denotes the set of elements in
![]() $\mathbb {Q}(\Gamma _{\mathrm {div}})$
with length
$\mathbb {Q}(\Gamma _{\mathrm {div}})$
with length
![]() $\leq N$
. Concretely, each
$\leq N$
. Concretely, each
![]() $x\in l_N(\Gamma )\backslash \{0\}$
with length l can express as
$x\in l_N(\Gamma )\backslash \{0\}$
with length l can express as
![]() $x=\sum _{j=1}^l x_j \prod _{t=1}^b \alpha _t^{k_{j,t}/d}$
, where
$x=\sum _{j=1}^l x_j \prod _{t=1}^b \alpha _t^{k_{j,t}/d}$
, where
![]() $x_j\in K_\Gamma ^*, d\in \mathbb {N}$
and
$x_j\in K_\Gamma ^*, d\in \mathbb {N}$
and
![]() $k_{j,t}\in \mathbb {Z}$
. We also recall that
$k_{j,t}\in \mathbb {Z}$
. We also recall that
![]() $U(\Gamma )$
is the set of elements in
$U(\Gamma )$
is the set of elements in
![]() $\overline {\mathbb {Q}}^*$
for which all its conjugates over
$\overline {\mathbb {Q}}^*$
for which all its conjugates over
![]() $K_\Gamma $
are concyclic and located on a circle centered at the origin. Finally, recall that for any algebraic set X, we define
$K_\Gamma $
are concyclic and located on a circle centered at the origin. Finally, recall that for any algebraic set X, we define
![]() $X.\Gamma _{\mathrm {div}}$
as the set of
$X.\Gamma _{\mathrm {div}}$
as the set of
![]() $x\gamma $
with
$x\gamma $
with
![]() $x\in X$
and
$x\in X$
and
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Proposition 5.2 There is
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $l_N(\Gamma )\cap U(\Gamma )\subset K_\Gamma (\mathcal {F}^{1/m})^*.\Gamma _{\mathrm {div}}$
.
$l_N(\Gamma )\cap U(\Gamma )\subset K_\Gamma (\mathcal {F}^{1/m})^*.\Gamma _{\mathrm {div}}$
.
Proof Let
![]() $x\in l_N(\Gamma )\cap U(\Gamma )$
be an element of length
$x\in l_N(\Gamma )\cap U(\Gamma )$
be an element of length
![]() $l\leq N$
that we express as above. For each
$l\leq N$
that we express as above. For each
![]() $t\in \{1,\dots ,b\}$
, set
$t\in \{1,\dots ,b\}$
, set
![]() $j_t\in \{1,\dots ,l\}$
such that
$j_t\in \{1,\dots ,l\}$
such that
![]() $k_{j_t,t}=\min \{k_{1,t},\dots , k_{l,t}\}$
. Let
$k_{j_t,t}=\min \{k_{1,t},\dots , k_{l,t}\}$
. Let
![]() $D_t$
denote the greatest common divisor of
$D_t$
denote the greatest common divisor of
![]() $k_{1,t}-k_{j_t,t}, \dots , k_{l,t}-k_{j_t,t}$
and d, then
$k_{1,t}-k_{j_t,t}, \dots , k_{l,t}-k_{j_t,t}$
and d, then
![]() $c_{j,t}= (k_{j,t}-k_{j_t,t})/D_t$
and
$c_{j,t}= (k_{j,t}-k_{j_t,t})/D_t$
and
![]() $d_t=d/D_t$
. By construction,
$d_t=d/D_t$
. By construction,
![]() $c_{1,t},\dots ,c_{l,t}$
and
$c_{1,t},\dots ,c_{l,t}$
and
![]() $d_t$
have no common positive factors other than
$d_t$
have no common positive factors other than
![]() $1$
for all
$1$
for all
![]() $t\in \{1,\dots ,r\}$
. Finally, set
$t\in \{1,\dots ,r\}$
. Finally, set
 $$ \begin{align} y= \sum_{j=1}^l x_j \prod_{t=1}^b \alpha_t^{c_{j,t}/d_t} \; \; \text{and} \; \; z=\prod_{t=1}^b \alpha_t^{k_{j_t,t}/d}\in \Gamma_{\mathrm{div}}. \end{align} $$
$$ \begin{align} y= \sum_{j=1}^l x_j \prod_{t=1}^b \alpha_t^{c_{j,t}/d_t} \; \; \text{and} \; \; z=\prod_{t=1}^b \alpha_t^{k_{j_t,t}/d}\in \Gamma_{\mathrm{div}}. \end{align} $$
We easily check that
![]() $x=yz$
. As
$x=yz$
. As
![]() $z\in \Gamma _{\mathrm {div}}$
, Lemma 5.1 tells us that y has length l too. Let
$z\in \Gamma _{\mathrm {div}}$
, Lemma 5.1 tells us that y has length l too. Let
![]() $s\in \{1,\dots ,b\}$
be such that
$s\in \{1,\dots ,b\}$
be such that
![]() $d_s=\max \{d_1,\dots ,d_b\}$
. If
$d_s=\max \{d_1,\dots ,d_b\}$
. If
![]() $d_s$
is bounded from above by a constant c depending only on
$d_s$
is bounded from above by a constant c depending only on
![]() $\Gamma $
and N, then (6) would show that
$\Gamma $
and N, then (6) would show that
![]() $y\in K_\Gamma (\mathcal {F}^{1/c!})$
. The proposition with
$y\in K_\Gamma (\mathcal {F}^{1/c!})$
. The proposition with
![]() $m=c !$
would follow since
$m=c !$
would follow since
![]() $x=yz$
with
$x=yz$
with
![]() $z\in \Gamma _{\mathrm {div}}$
.
$z\in \Gamma _{\mathrm {div}}$
.
Put
![]() $\{b_1,\dots ,b_n\}=\{c_{1,s}, \dots , c_{l,s}\}$
, where
$\{b_1,\dots ,b_n\}=\{c_{1,s}, \dots , c_{l,s}\}$
, where
![]() $b_1,\dots ,b_n$
are pairwise distinct. We can assume that
$b_1,\dots ,b_n$
are pairwise distinct. We can assume that
![]() $b_1=c_{j_s,s}$
. For all
$b_1=c_{j_s,s}$
. For all
![]() $k\in \{1,\dots , n\}$
, write
$k\in \{1,\dots , n\}$
, write
![]() $E_k$
the set of
$E_k$
the set of
![]() $j\in \{1,\dots ,l\}$
such that
$j\in \{1,\dots ,l\}$
such that
![]() $b_k=c_{j,s}$
. Clearly
$b_k=c_{j,s}$
. Clearly
![]() $E_1,\dots , E_n$
is a partition of
$E_1,\dots , E_n$
is a partition of
![]() $\{1,\dots ,l\}$
.
$\{1,\dots ,l\}$
.
Lemma 2.1 applied to
![]() $L=\mathbb {Q}(\Gamma )$
and
$L=\mathbb {Q}(\Gamma )$
and
![]() $m=\infty $
as well as the multiplicativity formula for degrees claim that the extension
$m=\infty $
as well as the multiplicativity formula for degrees claim that the extension
has degree at least
![]() $d_s/C$
for some
$d_s/C$
for some
![]() $C>0$
depending only on
$C>0$
depending only on
![]() $\Gamma $
. Its Galois group is therefore isomorphic to
$\Gamma $
. Its Galois group is therefore isomorphic to
![]() $\mathbb {Z}/(d_s/c)\mathbb {Z}$
for some
$\mathbb {Z}/(d_s/c)\mathbb {Z}$
for some
![]() $c\leq C$
. Put
$c\leq C$
. Put
 $$\begin{align*}y_j= x_j \prod_{t=1, t\neq s}^b \alpha_t^{c_{j,t}/d_t}\in M, v_k=\sum_{j\in E_k} y_j, a_k=v_k\alpha_s^{b_k/d_s} \; \text{and} \; f(z)=\sum_{k=1}^n (a_k/y) z^{b_k}.\end{align*}$$
$$\begin{align*}y_j= x_j \prod_{t=1, t\neq s}^b \alpha_t^{c_{j,t}/d_t}\in M, v_k=\sum_{j\in E_k} y_j, a_k=v_k\alpha_s^{b_k/d_s} \; \text{and} \; f(z)=\sum_{k=1}^n (a_k/y) z^{b_k}.\end{align*}$$
Note that
![]() $y = \sum _{j=1}^l y_j \alpha _s^{c_{j,s}/d_s}$
. Establish below that
$y = \sum _{j=1}^l y_j \alpha _s^{c_{j,s}/d_s}$
. Establish below that
![]() $d_s/c\in \mathcal {S}_n$
(see Definition 4.1).
$d_s/c\in \mathcal {S}_n$
(see Definition 4.1).
First,
![]() $c_{j_s,s}=0$
by definition of
$c_{j_s,s}=0$
by definition of
![]() $c_{j,t}$
; whence
$c_{j,t}$
; whence
![]() $b_1=0$
. Next,
$b_1=0$
. Next,
![]() $b_1,\dots ,b_n$
and
$b_1,\dots ,b_n$
and
![]() $d_s/c$
have no common positive factors other than
$d_s/c$
have no common positive factors other than
![]() $1$
by construction of
$1$
by construction of
![]() $c_{1,s}, \dots , c_{l,s}$
and
$c_{1,s}, \dots , c_{l,s}$
and
![]() $d_s$
.
$d_s$
.
Assume that
![]() $\sum _{k\in I}a_k=0$
for some subset
$\sum _{k\in I}a_k=0$
for some subset
![]() $I\subset \{1,\dots ,n\}$
. Then
$I\subset \{1,\dots ,n\}$
. Then
which allows us to deduce that
 $$\begin{align*}y=\sum_{j=1}^l y_j \alpha_s^{c_{j,s}/d_s} = \sum_{j\notin \bigsqcup_{k\in I} E_k} y_j\alpha_s^{c_{j,s}/d_s} = \sum_{j\notin \bigsqcup_{k\in I} E_k} x_j\prod_{t=1}^b \alpha_t^{c_{j,t}/d_t}.\end{align*}$$
$$\begin{align*}y=\sum_{j=1}^l y_j \alpha_s^{c_{j,s}/d_s} = \sum_{j\notin \bigsqcup_{k\in I} E_k} y_j\alpha_s^{c_{j,s}/d_s} = \sum_{j\notin \bigsqcup_{k\in I} E_k} x_j\prod_{t=1}^b \alpha_t^{c_{j,t}/d_t}.\end{align*}$$
The definition of the length proves that y has length at most
![]() $l-\# \bigsqcup _{k\in I} E_k$
. As y has length l and
$l-\# \bigsqcup _{k\in I} E_k$
. As y has length l and
![]() $E_1,\dots ,E_n$
are non-empty sets, we conclude that I is empty. The contrapositive proves that
$E_1,\dots ,E_n$
are non-empty sets, we conclude that I is empty. The contrapositive proves that
![]() $\sum _{k\in I} a_k \neq 0$
for all non-empty subsets
$\sum _{k\in I} a_k \neq 0$
for all non-empty subsets
![]() $I\subset \{1,\dots , n\}$
.
$I\subset \{1,\dots , n\}$
.
Let
![]() $\sigma \in \mathrm {Gal}(L/M)$
. As
$\sigma \in \mathrm {Gal}(L/M)$
. As
![]() $y_j\in M$
for all j, we get
$y_j\in M$
for all j, we get
![]() $v_k\in M$
for all k. Collecting the information above, we obtain
$v_k\in M$
for all k. Collecting the information above, we obtain
 $$ \begin{align} \begin{aligned} \sigma y & = \sigma\left(\sum_{j=1}^l y_j \alpha_s^{c_{j,s}/d_s}\right) = \sigma\left(\sum_{k=1}^n \sum_{j\in E_k} y_j \alpha_s^{c_{j,s}/d_s}\right) \\ & = \sigma\left(\sum_{k=1}^n v_k \alpha_s^{b_k/d_s}\right)= \sum_{k=1}^n v_k \alpha_s^{b_k/d_s} \zeta_{d_s/c}^{b_k l_\sigma}=y f(\zeta_{d_s/c}^{l_\sigma}) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sigma y & = \sigma\left(\sum_{j=1}^l y_j \alpha_s^{c_{j,s}/d_s}\right) = \sigma\left(\sum_{k=1}^n \sum_{j\in E_k} y_j \alpha_s^{c_{j,s}/d_s}\right) \\ & = \sigma\left(\sum_{k=1}^n v_k \alpha_s^{b_k/d_s}\right)= \sum_{k=1}^n v_k \alpha_s^{b_k/d_s} \zeta_{d_s/c}^{b_k l_\sigma}=y f(\zeta_{d_s/c}^{l_\sigma}) \end{aligned} \end{align} $$
for some
![]() $l_\sigma \in \{1,\dots , d_s/c\}$
. Recall that
$l_\sigma \in \{1,\dots , d_s/c\}$
. Recall that
![]() $y=x/z$
, that
$y=x/z$
, that
![]() $x\in U(\Gamma )$
and that
$x\in U(\Gamma )$
and that
![]() $z\in \Gamma _{\mathrm {div}}\subset U(\Gamma )$
(see the introduction). As
$z\in \Gamma _{\mathrm {div}}\subset U(\Gamma )$
(see the introduction). As
![]() $U(\Gamma )$
is a group, we deduce that
$U(\Gamma )$
is a group, we deduce that
![]() $y\in U(\Gamma )$
, and so
$y\in U(\Gamma )$
, and so
![]() $\vert \sigma y\vert = \vert y \vert $
. By varying
$\vert \sigma y\vert = \vert y \vert $
. By varying
![]() $\sigma \in \mathrm {Gal}(L/M)$
, we infer thanks to (7) that
$\sigma \in \mathrm {Gal}(L/M)$
, we infer thanks to (7) that
![]() $\vert f(\zeta )\vert = 1$
for all
$\vert f(\zeta )\vert = 1$
for all
![]() $\zeta \in \mu _{d_s/c}$
. From all this, we finally conclude
$\zeta \in \mu _{d_s/c}$
. From all this, we finally conclude
![]() $d_s/c\in \mathcal {S}_n$
. By Theorem 4.3, we get
$d_s/c\in \mathcal {S}_n$
. By Theorem 4.3, we get
![]() $d_s/c \leq 4^n n^2$
, i.e.,
$d_s/c \leq 4^n n^2$
, i.e.,
![]() $d_s\leq 4^N N^2 C$
, which ends the proof of the proposition.
$d_s\leq 4^N N^2 C$
, which ends the proof of the proposition.
6 Equidistribution
As stated in the introduction, we will use equidistribution arguments to prove Theorem 1.7, and especially Corollary 6.2. This section is therefore devoted to the proof of this corollary.
In this section,
![]() $M\in \mathbb {N}$
denotes a positive integer. The Weil height can extend to
$M\in \mathbb {N}$
denotes a positive integer. The Weil height can extend to
![]() $\overline {\mathbb {Q}}^M$
, see [Reference Bombieri and Gubler8, Section 1.5]; call it h again. We have
$\overline {\mathbb {Q}}^M$
, see [Reference Bombieri and Gubler8, Section 1.5]; call it h again. We have
![]() $h(\boldsymbol {\zeta })=0$
for all
$h(\boldsymbol {\zeta })=0$
for all
![]() $\boldsymbol {\zeta }\in \mu _\infty ^M$
.
$\boldsymbol {\zeta }\in \mu _\infty ^M$
.
We say that a sequence
![]() $(\mu _n)$
of probability measures on
$(\mu _n)$
of probability measures on
![]() $S=(\mathbb {C}^*)^M$
weakly converges to
$S=(\mathbb {C}^*)^M$
weakly converges to
![]() $\mu $
, denoted by
$\mu $
, denoted by
![]() $\mu _n \xrightarrow {w} \mu $
, if
$\mu _n \xrightarrow {w} \mu $
, if
![]() $\int _S f d\mu _n \to \int _S f d\mu $
for any bounded continuous function
$\int _S f d\mu _n \to \int _S f d\mu $
for any bounded continuous function
![]() $f : S \to \mathbb {R}$
. For a finite set
$f : S \to \mathbb {R}$
. For a finite set
![]() $F\subset S$
, the discrete probability measure on S associated with it is given by
$F\subset S$
, the discrete probability measure on S associated with it is given by
where
![]() $\delta _\alpha $
is the Dirac measure on S supported on
$\delta _\alpha $
is the Dirac measure on S supported on
![]() $\alpha $
.
$\alpha $
.
Write
![]() $\nu _M$
for the uniform probability measure on S supported at the unit polycircle
$\nu _M$
for the uniform probability measure on S supported at the unit polycircle
![]() $\vert z_1\vert = \dots = \vert z_M\vert =1$
, where it coincides with the normalized Haar measure.
$\vert z_1\vert = \dots = \vert z_M\vert =1$
, where it coincides with the normalized Haar measure.
Finally, we say that a sequence
![]() $(P_n)$
of
$(P_n)$
of
![]() $(\overline {\mathbb {Q}}^*)^M$
is strict if any proper algebraic subgroup of
$(\overline {\mathbb {Q}}^*)^M$
is strict if any proper algebraic subgroup of
![]() $(\overline {\mathbb {Q}}^*)^M$
contains
$(\overline {\mathbb {Q}}^*)^M$
contains
![]() $P_n$
for only finitely many n. When
$P_n$
for only finitely many n. When
![]() $M=1$
, it is equivalent to saying that
$M=1$
, it is equivalent to saying that
![]() $[\mathbb {Q}(P_n) : \mathbb {Q}] \to +\infty $
(see [Reference Petsche20, Lemma 5.2.1]).
$[\mathbb {Q}(P_n) : \mathbb {Q}] \to +\infty $
(see [Reference Petsche20, Lemma 5.2.1]).
The arguments presented by Bilu in [Reference Bilu6] are quite general and can easily be adapted to produce other equidistribution results. We see an example of this below.
Proposition 6.1 Let
![]() $(\zeta _{m_n}^{k_{1,n}},\dots ,\zeta _{m_n}^{k_{M,n}})$
be a strict sequence with
$(\zeta _{m_n}^{k_{1,n}},\dots ,\zeta _{m_n}^{k_{M,n}})$
be a strict sequence with
![]() $m_n\in \mathbb {N}$
and
$m_n\in \mathbb {N}$
and
![]() $k_{1,n},\dots ,k_{M,n}\in \mathbb {Z}$
for all n. Then
$k_{1,n},\dots ,k_{M,n}\in \mathbb {Z}$
for all n. Then
![]() $\mu _{E_n} \xrightarrow {w} \nu _M$
, where
$\mu _{E_n} \xrightarrow {w} \nu _M$
, where
Proof First of all, we alert the reader on the fact that the hypothesis “
![]() $F_n$
are pairwise distinct” made in [Reference Favre and Rivera-Letelier10, Théorème 2] can be weakened in
$F_n$
are pairwise distinct” made in [Reference Favre and Rivera-Letelier10, Théorème 2] can be weakened in
![]() $\#F_n \to +\infty $
, the former assumption being only used to get the latter one (see [Reference Favre and Rivera-Letelier10, Sous-section 5.4]).
$\#F_n \to +\infty $
, the former assumption being only used to get the latter one (see [Reference Favre and Rivera-Letelier10, Sous-section 5.4]).
Let
![]() $\mathbf {n}=(n_1,\dots ,n_M)\in \mathbb {Z}^M\backslash \{(0,\dots ,0)\}$
, and set
$\mathbf {n}=(n_1,\dots ,n_M)\in \mathbb {Z}^M\backslash \{(0,\dots ,0)\}$
, and set
![]() $\chi _{\mathbf {n}} : S \to \mathbb {C}$
to be the function defined by
$\chi _{\mathbf {n}} : S \to \mathbb {C}$
to be the function defined by
![]() $\chi _{\mathbf {n}}(z_1,\dots ,z_M)=\prod _{i=1}^M z_i^{n_i}$
. We clearly have
$\chi _{\mathbf {n}}(z_1,\dots ,z_M)=\prod _{i=1}^M z_i^{n_i}$
. We clearly have
The sequence
![]() $(\zeta _{m_n}^{\sum _{i=1}^M n_i k_{i,n}})$
is strict since
$(\zeta _{m_n}^{\sum _{i=1}^M n_i k_{i,n}})$
is strict since
![]() $((\zeta _{m_n}^{k_{1,n}},\dots ,\zeta _{m_n}^{k_{M,n}}))$
is by hypothesis. Thus
$((\zeta _{m_n}^{k_{1,n}},\dots ,\zeta _{m_n}^{k_{M,n}}))$
is by hypothesis. Thus
Thanks to [Reference Favre and Rivera-Letelier10, Théorème 2], we get
![]() $\mu _{\chi _{\mathbf {n}}(E_n)} \xrightarrow {w} \nu _1$
. From this observation, and following the lines of the proof of [Reference Bilu6, Proposition 4.1], we conclude that [Reference Bilu6, Proposition 4.1] also holds for the sequence
$\mu _{\chi _{\mathbf {n}}(E_n)} \xrightarrow {w} \nu _1$
. From this observation, and following the lines of the proof of [Reference Bilu6, Proposition 4.1], we conclude that [Reference Bilu6, Proposition 4.1] also holds for the sequence
![]() $(\mu _{E_n})$
.
$(\mu _{E_n})$
.
For
![]() $z=(z_1,\dots ,z_M)\in S$
, put
$z=(z_1,\dots ,z_M)\in S$
, put
![]() $\vert z\vert _\infty = \max \{\vert z_1\vert , \dots , \vert z_M\vert \}$
. Let
$\vert z\vert _\infty = \max \{\vert z_1\vert , \dots , \vert z_M\vert \}$
. Let
![]() $\varepsilon>0$
and write
$\varepsilon>0$
and write
Let A be the family of sets
![]() $E\subset (\overline {\mathbb {Q}}^*)^M$
that are finite,
$E\subset (\overline {\mathbb {Q}}^*)^M$
that are finite,
![]() $\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})$
-invariant and such that
$\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})$
-invariant and such that
![]() $h(\boldsymbol {\beta }),h(\boldsymbol {\beta }^{-1}) \leq 1$
for all
$h(\boldsymbol {\beta }),h(\boldsymbol {\beta }^{-1}) \leq 1$
for all
![]() $\boldsymbol {\beta }\in E$
. We clearly have
$\boldsymbol {\beta }\in E$
. We clearly have
![]() $E_n\in A$
for all n.
$E_n\in A$
for all n.
Choose
![]() $E\in A$
. As E is both finite and
$E\in A$
. As E is both finite and
![]() $\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})$
-invariant, we can decompose it as a finite disjoint union of Galois orbits
$\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})$
-invariant, we can decompose it as a finite disjoint union of Galois orbits
![]() $\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q}).\boldsymbol {\beta }_1, \dots , \mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q}).\boldsymbol {\beta }_k$
for some
$\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q}).\boldsymbol {\beta }_1, \dots , \mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q}).\boldsymbol {\beta }_k$
for some
![]() $\boldsymbol {\beta }_1,\dots ,\boldsymbol {\beta }_k\in E$
. For each
$\boldsymbol {\beta }_1,\dots ,\boldsymbol {\beta }_k\in E$
. For each
![]() $i\in \{1,\dots ,k\}$
, Bilu proved in [Reference Bilu6, Section 4] that
$i\in \{1,\dots ,k\}$
, Bilu proved in [Reference Bilu6, Section 4] that
![]() $\sigma \boldsymbol {\beta }_i \notin K_\varepsilon $
for at most
$\sigma \boldsymbol {\beta }_i \notin K_\varepsilon $
for at most
![]() $\varepsilon [\mathbb {Q}(\boldsymbol {\beta }_i) : \mathbb {Q}]$
field embeddings
$\varepsilon [\mathbb {Q}(\boldsymbol {\beta }_i) : \mathbb {Q}]$
field embeddings
![]() $\sigma : \mathbb {Q}(\boldsymbol {\beta }_i) \to \mathbb {C}$
. Thus,
$\sigma : \mathbb {Q}(\boldsymbol {\beta }_i) \to \mathbb {C}$
. Thus,
![]() $E\backslash K_\varepsilon $
has at most
$E\backslash K_\varepsilon $
has at most
![]() $\varepsilon \sum _{i=1}^k [\mathbb {Q}(\boldsymbol {\beta }_i) : \mathbb {Q}]=\varepsilon \#E$
elements, i.e.,
$\varepsilon \sum _{i=1}^k [\mathbb {Q}(\boldsymbol {\beta }_i) : \mathbb {Q}]=\varepsilon \#E$
elements, i.e.,
![]() $\mu _E(K_\varepsilon ) \geq 1-\varepsilon $
. It remains to mimic the proof of [Reference Bilu6, Theorem 1.1] made in [Reference Bilu6, Section 4] to deduce the proposition.
$\mu _E(K_\varepsilon ) \geq 1-\varepsilon $
. It remains to mimic the proof of [Reference Bilu6, Theorem 1.1] made in [Reference Bilu6, Section 4] to deduce the proposition.
For
![]() $\zeta , \zeta '$
belonging to the unit circle in
$\zeta , \zeta '$
belonging to the unit circle in
![]() $\mathbb {C}$
, we denote by
$\mathbb {C}$
, we denote by
![]() $[\zeta , \zeta ']$
the arc of this unit circle connecting
$[\zeta , \zeta ']$
the arc of this unit circle connecting
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
anticlockwise.
$\zeta '$
anticlockwise.
Corollary 6.2 Let
![]() $(\zeta _{m_n}^{k_{1,n}}, \dots ,\zeta _{m_n}^{k_{M,n}})$
be a strict sequence, with
$(\zeta _{m_n}^{k_{1,n}}, \dots ,\zeta _{m_n}^{k_{M,n}})$
be a strict sequence, with
![]() $m_n\in \mathbb {N}$
and
$m_n\in \mathbb {N}$
and
![]() $k_{1,n}, \dots , k_{M,n} \in \mathbb {Z}$
for all n. Let
$k_{1,n}, \dots , k_{M,n} \in \mathbb {Z}$
for all n. Let
![]() $\varepsilon>0$
, and let
$\varepsilon>0$
, and let
![]() $x_1,\dots ,x_M\in [0; 2\pi ]$
. Write
$x_1,\dots ,x_M\in [0; 2\pi ]$
. Write
![]() $V=\prod _{j=1}^M [ e^{\zeta _4(x_j-\varepsilon )}; e^{\zeta _4(x_j+\varepsilon )}]$
and denote by
$V=\prod _{j=1}^M [ e^{\zeta _4(x_j-\varepsilon )}; e^{\zeta _4(x_j+\varepsilon )}]$
and denote by
![]() $\mathcal {K}_n(V),$
the set of
$\mathcal {K}_n(V),$
the set of
![]() $r\in \mathbb {Z}/m_n\mathbb {Z}$
such that
$r\in \mathbb {Z}/m_n\mathbb {Z}$
such that
![]() $(\zeta _{m_n}^{r k_{1,n}}, \dots , \zeta _{m_n}^{r k_{M,n}}) \in V$
. Then, for all n large enough, we have
$(\zeta _{m_n}^{r k_{1,n}}, \dots , \zeta _{m_n}^{r k_{M,n}}) \in V$
. Then, for all n large enough, we have
 $$\begin{align*}\frac{\# \mathcal{K}_n (V)}{m_n} \geq (1-\varepsilon) \left(\frac{\varepsilon}{2\pi}\right)^M. \end{align*}$$
$$\begin{align*}\frac{\# \mathcal{K}_n (V)}{m_n} \geq (1-\varepsilon) \left(\frac{\varepsilon}{2\pi}\right)^M. \end{align*}$$
Proof Let
![]() $f : \mathbb {C}^M \to [0;1]$
be any continuous function that is identically zero outside V and taking the value
$f : \mathbb {C}^M \to [0;1]$
be any continuous function that is identically zero outside V and taking the value
![]() $1$
on
$1$
on
 $$\begin{align*}W =\prod_{j=1}^M [ e^{\zeta_4(x_j-\varepsilon/2)}; e^{\zeta_4 (x_j+\varepsilon/2)}]\subsetneq V.\end{align*}$$
$$\begin{align*}W =\prod_{j=1}^M [ e^{\zeta_4(x_j-\varepsilon/2)}; e^{\zeta_4 (x_j+\varepsilon/2)}]\subsetneq V.\end{align*}$$
Let
![]() $n\in \mathbb {N}$
. For
$n\in \mathbb {N}$
. For
![]() $r\in \mathbb {Z}$
, we set
$r\in \mathbb {Z}$
, we set
Let
![]() $r_n$
be the smallest divisor of
$r_n$
be the smallest divisor of
![]() $m_n$
such that
$m_n$
such that
![]() $r_n k_{j,n} \equiv 0 \; (m_n)$
for all
$r_n k_{j,n} \equiv 0 \; (m_n)$
for all
![]() $j\in \{1,\dots ,M\}$
. Thanks to the equality
$j\in \{1,\dots ,M\}$
. Thanks to the equality
![]() $P_{r+r_n,n}=P_{r,n}$
, valid for all
$P_{r+r_n,n}=P_{r,n}$
, valid for all
![]() $r\in \mathbb {Z}$
, we infer that
$r\in \mathbb {Z}$
, we infer that
![]() $E_n = \{ P_{r,n}, r=1,\dots ,r_n \}$
. Furthermore, the minimality of
$E_n = \{ P_{r,n}, r=1,\dots ,r_n \}$
. Furthermore, the minimality of
![]() $r_n$
gives
$r_n$
gives
![]() $\# E_n = r_n$
. Thus
$\# E_n = r_n$
. Thus
 $$\begin{align*}\frac{1}{ m_n} \sum_{r=1}^{m_n} \delta_{P_{r,n}} = \frac{1}{r_n}\sum_{r=1}^{r_n} \delta_{P_{r,n}} = \mu_{E_n}. \end{align*}$$
$$\begin{align*}\frac{1}{ m_n} \sum_{r=1}^{m_n} \delta_{P_{r,n}} = \frac{1}{r_n}\sum_{r=1}^{r_n} \delta_{P_{r,n}} = \mu_{E_n}. \end{align*}$$
Combining this equality with Proposition 6.1 provides the limit
 $$\begin{align*}u_n= \frac{1}{m_n}\sum_{r=1}^{m_n} f(P_{r,n}) =\frac{1}{\#E_n}\sum_{\alpha\in E_n} f(\alpha) \to \int f d\nu_M,\end{align*}$$
$$\begin{align*}u_n= \frac{1}{m_n}\sum_{r=1}^{m_n} f(P_{r,n}) =\frac{1}{\#E_n}\sum_{\alpha\in E_n} f(\alpha) \to \int f d\nu_M,\end{align*}$$
since the sequence
![]() $(P_{1,n})$
is strict by assumption. Thus,
$(P_{1,n})$
is strict by assumption. Thus,
![]() $u_n\geq (1-\varepsilon )\int f d\nu _M$
for all n large enough. The lemma follows by noticing that the construction of f implies the inequalities
$u_n\geq (1-\varepsilon )\int f d\nu _M$
for all n large enough. The lemma follows by noticing that the construction of f implies the inequalities
![]() $u_n \leq \frac {1}{m_n}\#\mathcal {K}_n(V)$
and
$u_n \leq \frac {1}{m_n}\#\mathcal {K}_n(V)$
and
![]() $\int f d\nu _M \geq \nu _M(W)=(\varepsilon /2\pi )^M$
.
$\int f d\nu _M \geq \nu _M(W)=(\varepsilon /2\pi )^M$
.
7 A crucial subsequence
To prove our Theorem 1.7, we need to extract from
![]() $(x_n)$
a “good” subsequence whose construction is the aim of this section.
$(x_n)$
a “good” subsequence whose construction is the aim of this section.
Recall that we fixed an integer
![]() $N\in \mathbb {N}$
and a generating set
$N\in \mathbb {N}$
and a generating set
![]() $\{\alpha _1,\dots ,\alpha _b\}$
of the torsion-free part of
$\{\alpha _1,\dots ,\alpha _b\}$
of the torsion-free part of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $(x_n)$
be a sequence of
$(x_n)$
be a sequence of
![]() $l_N(\Gamma )$
(see the introduction for a definition). Each term can express as
$l_N(\Gamma )$
(see the introduction for a definition). Each term can express as
 $$\begin{align*}x_n= \sum_{j=1}^N x_{j,n}\prod_{l=1}^b \alpha_l^{k_{j,l,n}/m_n}\end{align*}$$
$$\begin{align*}x_n= \sum_{j=1}^N x_{j,n}\prod_{l=1}^b \alpha_l^{k_{j,l,n}/m_n}\end{align*}$$
with
![]() $x_{j,n}\in K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma ), m_n \in \mathbb {N}$
and
$x_{j,n}\in K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma ), m_n \in \mathbb {N}$
and
![]() $k_{j,l,n}\in \mathbb {Z}$
.
$k_{j,l,n}\in \mathbb {Z}$
.
By convention, a sum indexed by the empty set is always
![]() $0$
.
$0$
.
Lemma 7.1 There exists a subsequence
![]() $(x_{\psi (n)})$
of
$(x_{\psi (n)})$
of
![]() $(x_n)$
satisfying the following: for all
$(x_n)$
satisfying the following: for all
![]() $l\in \{1,\dots ,b\}$
, there is a set
$l\in \{1,\dots ,b\}$
, there is a set
![]() $J_l\subset \{1,\dots ,N\}$
such that:
$J_l\subset \{1,\dots ,N\}$
such that:
-
(a) the sequence of terms
 $(\zeta _{m_{\psi (n)}}^{k_{j,l,\psi (n)}})_{j\in J_l}$
is strict unless
$(\zeta _{m_{\psi (n)}}^{k_{j,l,\psi (n)}})_{j\in J_l}$
is strict unless
 $J_l$
is empty;
$J_l$
is empty; -
(b) for all
 $j\in \{1,\dots ,N\}$
, there are an integer
$j\in \{1,\dots ,N\}$
, there are an integer
 $\lambda ^{(j,l)}\in \mathbb {Z}\backslash \{0\}$
and a tuple
$\lambda ^{(j,l)}\in \mathbb {Z}\backslash \{0\}$
and a tuple
 $(\lambda _m^{(j,l)})_{m\in J_l}\in \mathbb {Z}^{\#J_l}$
such that for all n,
$(\lambda _m^{(j,l)})_{m\in J_l}\in \mathbb {Z}^{\#J_l}$
such that for all n,  $$\begin{align*}\lambda^{(j,l)}k_{j,l,\psi(n)}+\sum_{m\in J_l} \lambda_m^{(j,l)} k_{m,l,\psi(n)}\equiv 0 \; (m_{\psi(n)}). \end{align*}$$
$$\begin{align*}\lambda^{(j,l)}k_{j,l,\psi(n)}+\sum_{m\in J_l} \lambda_m^{(j,l)} k_{m,l,\psi(n)}\equiv 0 \; (m_{\psi(n)}). \end{align*}$$
Proof We compare the elements in
![]() $\mathbb {R}^2$
with the lexicographic order
$\mathbb {R}^2$
with the lexicographic order
![]() $\preceq $
.
$\preceq $
.
Construct recursively sets
![]() $J_{l,t}\subset \{1,\dots ,N\}$
and functions
$J_{l,t}\subset \{1,\dots ,N\}$
and functions
![]() $\psi _{l,t} : \mathbb {N}\to \mathbb {N}$
, where
$\psi _{l,t} : \mathbb {N}\to \mathbb {N}$
, where
![]() $(l,t)$
ranges over all elements of
$(l,t)$
ranges over all elements of
![]() $I=\{1,\dots ,b\} \times \{0,\dots ,N\}$
, as follows: If
$I=\{1,\dots ,b\} \times \{0,\dots ,N\}$
, as follows: If
![]() $t=0$
, then
$t=0$
, then
![]() $J_{l,0}$
is empty and
$J_{l,0}$
is empty and
![]() $\psi _{l,0}$
is either the identity if
$\psi _{l,0}$
is either the identity if
![]() $l=1$
or
$l=1$
or
![]() $\psi _{l-1,N}$
if
$\psi _{l-1,N}$
if
![]() $l>1$
. Assume that
$l>1$
. Assume that
![]() $t\geq 1$
. If the sequence of terms
$t\geq 1$
. If the sequence of terms
 $\left (\zeta _{m_{\psi _{l,t-1}(n)}}^{k_{j,l,\psi _{l,t-1}(n)}}\right )_{j\in J_{l,t-1} \cup \{t\}}$
is strict, then we put
$\left (\zeta _{m_{\psi _{l,t-1}(n)}}^{k_{j,l,\psi _{l,t-1}(n)}}\right )_{j\in J_{l,t-1} \cup \{t\}}$
is strict, then we put
![]() $J_{l,t}=J_{l,t-1}\cup \{t\}$
and
$J_{l,t}=J_{l,t-1}\cup \{t\}$
and
![]() $\psi _{l,t}=\psi _{l,t-1}$
. If not, then put
$\psi _{l,t}=\psi _{l,t-1}$
. If not, then put
![]() $J_{l,t}=J_{l,t-1}$
. By definition of a strict sequence, there are a proper algebraic subgroup
$J_{l,t}=J_{l,t-1}$
. By definition of a strict sequence, there are a proper algebraic subgroup
![]() $T_{l,t}$
of
$T_{l,t}$
of
![]() $\overline {\mathbb {Q}}^*$
and a subsequence
$\overline {\mathbb {Q}}^*$
and a subsequence
![]() $(x_{\psi _{l,t}(n)})$
of
$(x_{\psi _{l,t}(n)})$
of
![]() $(x_{\psi _{l,t-1}(n)})$
such that
$(x_{\psi _{l,t-1}(n)})$
such that
 $u_{l,t,n}=\left (\zeta _{m_{\psi _{l,t}(n)}}^{k_{j,l,\psi _{l,t}(n)}}\right )_{j\in J_{l,t} \cup \{t\}}\in T_{l,t}$
for all n.
$u_{l,t,n}=\left (\zeta _{m_{\psi _{l,t}(n)}}^{k_{j,l,\psi _{l,t}(n)}}\right )_{j\in J_{l,t} \cup \{t\}}\in T_{l,t}$
for all n.
From this construction, we easily check by induction that for all
![]() $(l,t)\in I$
, either
$(l,t)\in I$
, either
![]() $J_{l,t}$
is empty or the sequence of terms
$J_{l,t}$
is empty or the sequence of terms
 $v_{l,t,n}=\left (\zeta _{m_{\psi _{l,t}(n)}}^{k_{j,l,\psi _{l,t}(n)}}\right )_{j\in J_{l,t}}$
is strict.
$v_{l,t,n}=\left (\zeta _{m_{\psi _{l,t}(n)}}^{k_{j,l,\psi _{l,t}(n)}}\right )_{j\in J_{l,t}}$
is strict.
Let
![]() $(i,j)\in I$
. Note that
$(i,j)\in I$
. Note that
![]() $(x_{\psi _{l,t'}(n)})$
is a subsequence of
$(x_{\psi _{l,t'}(n)})$
is a subsequence of
![]() $(x_{\psi _{l,t}(n)})$
if
$(x_{\psi _{l,t}(n)})$
if
![]() $t'\geq t$
. As
$t'\geq t$
. As
![]() $\psi _{l,0}=\psi _{l-1,N}$
if
$\psi _{l,0}=\psi _{l-1,N}$
if
![]() $l>1$
, an easy induction proves that
$l>1$
, an easy induction proves that
![]() $(x_{\psi _{l', t'}(n)})$
is a subsequence of
$(x_{\psi _{l', t'}(n)})$
is a subsequence of
![]() $(x_{\psi _{l,t}(n)})$
for all
$(x_{\psi _{l,t}(n)})$
for all
![]() $(l',t')\succeq (l,t)$
. In particular,
$(l',t')\succeq (l,t)$
. In particular,
![]() $(x_{\psi _{b,N}(n)})$
is a subsequence of
$(x_{\psi _{b,N}(n)})$
is a subsequence of
![]() $(x_{\psi _{l,t}(n)})$
.
$(x_{\psi _{l,t}(n)})$
.
Let
![]() $l\in \{1,\dots ,b\}$
and show that the lemma holds with
$l\in \{1,\dots ,b\}$
and show that the lemma holds with
![]() $J_l=J_{l,N}$
and
$J_l=J_{l,N}$
and
![]() $\psi =\psi _{b,N}$
.
$\psi =\psi _{b,N}$
.
![]() $(a)$
: By the foregoing, either
$(a)$
: By the foregoing, either
![]() $J_l$
is empty or
$J_l$
is empty or
![]() $(v_{l,N,n})$
is strict. Item
$(v_{l,N,n})$
is strict. Item
![]() $(a)$
follows since
$(a)$
follows since
![]() $(x_{\psi (n)})$
is a subsequence of
$(x_{\psi (n)})$
is a subsequence of
![]() $(x_{\psi _{l,N}(n)})$
.
$(x_{\psi _{l,N}(n)})$
.
![]() $(b)$
: If
$(b)$
: If
![]() $j\in J_l$
, then we get
$j\in J_l$
, then we get
![]() $(b)$
by taking
$(b)$
by taking
![]() $\lambda ^{(j,l)}=1, \lambda _j^{(j,l)} = -1$
and
$\lambda ^{(j,l)}=1, \lambda _j^{(j,l)} = -1$
and
![]() $\lambda _m^{(j,l)}=0$
if
$\lambda _m^{(j,l)}=0$
if
![]() $m\neq j$
. If
$m\neq j$
. If
![]() $j\notin J_l$
, then
$j\notin J_l$
, then
![]() $j\notin J_{l,j}$
since
$j\notin J_{l,j}$
since
![]() $J_{l,j}\subset J_l$
. By construction of
$J_{l,j}\subset J_l$
. By construction of
![]() $J_{l,j}$
, it means that
$J_{l,j}$
, it means that
![]() $u_{l,j,n}\in T_{l,j}$
for all n. Consequently, [Reference Onishchik and Winberg17, Chapter 3, §3, Theorem 5] says us that there exists a tuple
$u_{l,j,n}\in T_{l,j}$
for all n. Consequently, [Reference Onishchik and Winberg17, Chapter 3, §3, Theorem 5] says us that there exists a tuple
![]() $\boldsymbol {\lambda }=(\lambda _m^{(j,l)})_{m\in J_{l,j}\cup \{j\}}\in \mathbb {Z}^{1+\#J_{l,j}}\backslash \{(0,\dots ,0)\}$
such that for all n,
$\boldsymbol {\lambda }=(\lambda _m^{(j,l)})_{m\in J_{l,j}\cup \{j\}}\in \mathbb {Z}^{1+\#J_{l,j}}\backslash \{(0,\dots ,0)\}$
such that for all n,
To get
![]() $(b)$
, it remains to prove that
$(b)$
, it remains to prove that
![]() $\lambda _j^{(j,l)}\neq 0$
, which is clear if
$\lambda _j^{(j,l)}\neq 0$
, which is clear if
![]() $J_{l,j}$
is empty since
$J_{l,j}$
is empty since
![]() $\boldsymbol {\lambda }\neq 0$
. If not, then the sequence
$\boldsymbol {\lambda }\neq 0$
. If not, then the sequence
![]() $(v_{l,j,n})$
is strict. In particular,
$(v_{l,j,n})$
is strict. In particular,
![]() $v_{l,j,n}\in T_{l,j}$
for only finitely many n. Once again, [Reference Onishchik and Winberg17, Chapter 3, §3, Theorem 5] tells us that the congruence
$v_{l,j,n}\in T_{l,j}$
for only finitely many n. Once again, [Reference Onishchik and Winberg17, Chapter 3, §3, Theorem 5] tells us that the congruence
![]() $\sum _{m\in J_{l,j}} \lambda _m^{(j,l)} k_{m,l,\psi _{l,j}(n)} \equiv 0 \; (m_{\psi _{l,j}(n)})$
holds for only finitely many n, and (8) proves that
$\sum _{m\in J_{l,j}} \lambda _m^{(j,l)} k_{m,l,\psi _{l,j}(n)} \equiv 0 \; (m_{\psi _{l,j}(n)})$
holds for only finitely many n, and (8) proves that
![]() $\lambda _j^{(j,l)}\neq 0$
. This completes the proof.
$\lambda _j^{(j,l)}\neq 0$
. This completes the proof.
Put
![]() $O=(0,0)$
. For a point
$O=(0,0)$
. For a point
![]() $P\in \mathbb {R}^2$
with affix z, we set
$P\in \mathbb {R}^2$
with affix z, we set
![]() $\overrightarrow {z}=\overrightarrow {OP}$
. Next define
$\overrightarrow {z}=\overrightarrow {OP}$
. Next define
![]() $(\overrightarrow {z_1}, \overrightarrow {z_2})$
to be the angle formed by nonzero vectors
$(\overrightarrow {z_1}, \overrightarrow {z_2})$
to be the angle formed by nonzero vectors
![]() $\overrightarrow {z_1}$
and
$\overrightarrow {z_1}$
and
![]() $\overrightarrow {z_2}$
. If
$\overrightarrow {z_2}$
. If
![]() $z_1=0$
or
$z_1=0$
or
![]() $z_2=0$
, we write
$z_2=0$
, we write
![]() $(\overrightarrow {z_1}, \overrightarrow {z_2})=0$
. We can now construct our sequence
$(\overrightarrow {z_1}, \overrightarrow {z_2})=0$
. We can now construct our sequence
![]() $(x_{\Phi (n)})$
.
$(x_{\Phi (n)})$
.
Lemma 7.2 We keep the notation of Lemma 7.1. Put
![]() $\theta = \prod _{j=1}^N \prod _{l=1}^b \vert \lambda ^{(j,l)} \vert \in \mathbb {N}, \Lambda _m^{(j,l)}= - \theta \lambda _m^{(j,l)}/\lambda ^{(j, l)}\in \mathbb {Z}$
and
$\theta = \prod _{j=1}^N \prod _{l=1}^b \vert \lambda ^{(j,l)} \vert \in \mathbb {N}, \Lambda _m^{(j,l)}= - \theta \lambda _m^{(j,l)}/\lambda ^{(j, l)}\in \mathbb {Z}$
and
![]() $K_{j,l,\psi (n)}=\sum _{m\in J_l} \Lambda _m^{(j,l)} k_{m,l,\psi (n)}$
. Then there exist a subsequence
$K_{j,l,\psi (n)}=\sum _{m\in J_l} \Lambda _m^{(j,l)} k_{m,l,\psi (n)}$
. Then there exist a subsequence
![]() $(x_{\Phi (n)})$
of
$(x_{\Phi (n)})$
of
![]() $(x_{\psi (n)})$
and a subset
$(x_{\psi (n)})$
and a subset
![]() $I\subset \{1,\dots ,N\}$
such that:
$I\subset \{1,\dots ,N\}$
such that:
-
(a) for all n, we have
where $$\begin{align*}x_{\Phi(n)}= \sum_{j\in I} a_{j,\Phi(n)}\prod_{l=1}^b \alpha_l^{K_{j,l,\Phi(n)}/(\theta m_{\Phi(n)})}= \sum_{j\in I} z_{j, \Phi(n)},\end{align*}$$
$$\begin{align*}x_{\Phi(n)}= \sum_{j\in I} a_{j,\Phi(n)}\prod_{l=1}^b \alpha_l^{K_{j,l,\Phi(n)}/(\theta m_{\Phi(n)})}= \sum_{j\in I} z_{j, \Phi(n)},\end{align*}$$
 $a_{j,\Phi (n)}\in K_\Gamma (\mathcal {F}^{1/\theta })$
and
$a_{j,\Phi (n)}\in K_\Gamma (\mathcal {F}^{1/\theta })$
and
 $z_{j,\Phi (n)} = a_{j,\Phi (n)}\prod _{l=1}^b \alpha _l^{K_{j,l,\Phi (n)}/(\theta m_{\Phi (n)})}$
;
$z_{j,\Phi (n)} = a_{j,\Phi (n)}\prod _{l=1}^b \alpha _l^{K_{j,l,\Phi (n)}/(\theta m_{\Phi (n)})}$
;
-
(b) the tuples
 $(K_{j,1,\Phi (n)}, \dots , K_{j,b,\Phi (n)})$
are pairwise distinct when j ranges over all elements of I;
$(K_{j,1,\Phi (n)}, \dots , K_{j,b,\Phi (n)})$
are pairwise distinct when j ranges over all elements of I; -
(c) the sequence
 $(((\overrightarrow {z_{i,\Phi (n)}}, \overrightarrow {z_{j,\Phi (n)}}))_{i, j \in I})$
converges as
$(((\overrightarrow {z_{i,\Phi (n)}}, \overrightarrow {z_{j,\Phi (n)}}))_{i, j \in I})$
converges as
 $n\to +\infty $
.
$n\to +\infty $
.
Proof Let
![]() $l\in \{1,\dots ,b\}$
, and let
$l\in \{1,\dots ,b\}$
, and let
![]() $j\in \{1,\dots ,N\}$
. A small calculation involving Lemma 7.1
$j\in \{1,\dots ,N\}$
. A small calculation involving Lemma 7.1
![]() $(b)$
gives
$(b)$
gives
![]() $k_{j,l,\psi (n)}= (v_{j,l,\psi (n)} m_{\psi (n)} + K_{j,l,\psi (n)})/\theta $
for some
$k_{j,l,\psi (n)}= (v_{j,l,\psi (n)} m_{\psi (n)} + K_{j,l,\psi (n)})/\theta $
for some
![]() $v_{j,l,\psi (n)}\in \mathbb {Z}$
. Thus
$v_{j,l,\psi (n)}\in \mathbb {Z}$
. Thus
 $$ \begin{align*} x_{\psi(n)} & = \sum_{j=1}^N x_{j, \psi(n)} \prod_{l=1}^b \alpha_l^{k_{j,l,\psi(n)}/m_{\psi(n)}} \\ & = \sum_{j=1}^N \left(x_{j, \psi(n)} \prod_{l=1}^b \alpha_l^{v_{j,l,\psi(n)}/\theta}\right)\prod_{l=1}^b \alpha_l^{K_{j,l,\psi(n)}/(\theta m_{\psi(n)})}. \end{align*} $$
$$ \begin{align*} x_{\psi(n)} & = \sum_{j=1}^N x_{j, \psi(n)} \prod_{l=1}^b \alpha_l^{k_{j,l,\psi(n)}/m_{\psi(n)}} \\ & = \sum_{j=1}^N \left(x_{j, \psi(n)} \prod_{l=1}^b \alpha_l^{v_{j,l,\psi(n)}/\theta}\right)\prod_{l=1}^b \alpha_l^{K_{j,l,\psi(n)}/(\theta m_{\psi(n)})}. \end{align*} $$
Note that
![]() $x_{j, \psi (n)} \prod _{l=1}^b \alpha _l^{v_{j,l,\psi (n)}/\theta }\in K_\Gamma (\mathcal {F}^{1/\theta })$
. If two tuples
$x_{j, \psi (n)} \prod _{l=1}^b \alpha _l^{v_{j,l,\psi (n)}/\theta }\in K_\Gamma (\mathcal {F}^{1/\theta })$
. If two tuples
![]() $(K_{i,1,\psi (n)}, \dots , K_{i,b,\psi (n)})$
and
$(K_{i,1,\psi (n)}, \dots , K_{i,b,\psi (n)})$
and
![]() $(K_{j,1,\psi (n)}, \dots , K_{j,b,\psi (n)})$
are equal, we can then group the ith and the jth term in the last sum above into a single. By repeating this process as much as possible, we construct a set
$(K_{j,1,\psi (n)}, \dots , K_{j,b,\psi (n)})$
are equal, we can then group the ith and the jth term in the last sum above into a single. By repeating this process as much as possible, we construct a set
![]() $I_{\psi (n)}\subset \{1,\dots ,N\}$
such that
$I_{\psi (n)}\subset \{1,\dots ,N\}$
such that
 $$\begin{align*}x_{\psi(n)}= \sum_{j\in I_{\psi(n)}} a_{j,\psi(n)}\prod_{l=1}^b \alpha_l^{K_{j,l,\psi(n)}/(\theta m_{\psi(n)})},\end{align*}$$
$$\begin{align*}x_{\psi(n)}= \sum_{j\in I_{\psi(n)}} a_{j,\psi(n)}\prod_{l=1}^b \alpha_l^{K_{j,l,\psi(n)}/(\theta m_{\psi(n)})},\end{align*}$$
where
![]() $a_{j,\psi (n)}\in K_\Gamma (\mathcal {F}^{1/\theta })$
and the tuples
$a_{j,\psi (n)}\in K_\Gamma (\mathcal {F}^{1/\theta })$
and the tuples
![]() $(K_{j,1,\psi (n)}, \dots , K_{j,b,\psi (n)})$
are pairwise distinct when j runs over all elements of
$(K_{j,1,\psi (n)}, \dots , K_{j,b,\psi (n)})$
are pairwise distinct when j runs over all elements of
![]() $I_{\psi (n)}$
. As
$I_{\psi (n)}$
. As
![]() $I_{\psi (n)}\subset \{1,\dots , N\}$
, there is a subsequence
$I_{\psi (n)}\subset \{1,\dots , N\}$
, there is a subsequence
![]() $(x_{\phi (n)})$
of
$(x_{\phi (n)})$
of
![]() $(x_{\psi (n)})$
for which the sequence
$(x_{\psi (n)})$
for which the sequence
![]() $(I_{\phi (n)})$
is constant, say to I.
$(I_{\phi (n)})$
is constant, say to I.
By definition,
![]() $(\overrightarrow {z_{i,\phi (n)}}, \overrightarrow {z_{j,\phi (n)}})\in [0, 2\pi [$
for all
$(\overrightarrow {z_{i,\phi (n)}}, \overrightarrow {z_{j,\phi (n)}})\in [0, 2\pi [$
for all
![]() $i,j\in I$
and all n. Hence, Bolzano–Weierstrass theorem ensures us the existence of a subsequence
$i,j\in I$
and all n. Hence, Bolzano–Weierstrass theorem ensures us the existence of a subsequence
![]() $(x_{\Phi (n)})$
of
$(x_{\Phi (n)})$
of
![]() $(x_{\phi (n)})$
such that the sequence
$(x_{\phi (n)})$
such that the sequence
![]() $(((\overrightarrow {z_{i,\Phi (n)}}, \overrightarrow {z_{j,\Phi (n)}}))_{i,j \in I})$
converges as
$(((\overrightarrow {z_{i,\Phi (n)}}, \overrightarrow {z_{j,\Phi (n)}}))_{i,j \in I})$
converges as
![]() $n\to +\infty $
. This proves
$n\to +\infty $
. This proves
![]() $(c)$
. Finally, we directly get
$(c)$
. Finally, we directly get
![]() $(a)$
and
$(a)$
and
![]() $(b)$
from the construction of
$(b)$
from the construction of
![]() $I_{\Phi (n)}=I$
.
$I_{\Phi (n)}=I$
.
8 Proof of Theorem 1.7
Recall that
![]() $l_N(\Gamma )$
is the set of
$l_N(\Gamma )$
is the set of
![]() $x\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
that can express as
$x\in \mathbb {Q}(\Gamma _{\mathrm {div}})$
that can express as
![]() $x=\sum _{j=1}^N x_j\gamma _j$
with
$x=\sum _{j=1}^N x_j\gamma _j$
with
![]() $x_j\in K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )$
and
$x_j\in K_\Gamma =\mathbb {Q}(\mu _\infty , \Gamma )$
and
![]() $\gamma _j\in \Gamma _{\mathrm {div}}$
. Clearly,
$\gamma _j\in \Gamma _{\mathrm {div}}$
. Clearly,
![]() $\tau x\in l_N(\Gamma )$
for all
$\tau x\in l_N(\Gamma )$
for all
![]() $\tau \in \mathrm {Gal}(\overline {\mathbb {Q}}/K_\Gamma )$
since any conjugate of
$\tau \in \mathrm {Gal}(\overline {\mathbb {Q}}/K_\Gamma )$
since any conjugate of
![]() $\gamma _j$
over
$\gamma _j$
over
![]() $K_\Gamma $
is equal to
$K_\Gamma $
is equal to
![]() $\gamma _j$
up to root of unity.
$\gamma _j$
up to root of unity.
Recall that
![]() $O_\Gamma (\alpha )$
and
$O_\Gamma (\alpha )$
and
![]() $d_{\Gamma , \varepsilon }(\alpha )$
have been defined in Section 1.2. Note that
$d_{\Gamma , \varepsilon }(\alpha )$
have been defined in Section 1.2. Note that
![]() $d_{\Gamma , \varepsilon }(\alpha )=d_{\Gamma , \varepsilon }(\beta )$
if
$d_{\Gamma , \varepsilon }(\alpha )=d_{\Gamma , \varepsilon }(\beta )$
if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are conjugates over
$\beta $
are conjugates over
![]() $K_\Gamma $
, that is if
$K_\Gamma $
, that is if
![]() $\beta \in O_\Gamma (\alpha )$
.
$\beta \in O_\Gamma (\alpha )$
.
The goal of this section is to prove the following.
Theorem 8.1 Let
![]() $(x_n)$
be a sequence of
$(x_n)$
be a sequence of
![]() $l_N(\Gamma )$
such that
$l_N(\Gamma )$
such that
![]() $d_{\Gamma , \varepsilon }(x_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
$d_{\Gamma , \varepsilon }(x_n)\underset {n\to +\infty }{\longrightarrow } 1$
for all
![]() $\varepsilon>0$
. Let
$\varepsilon>0$
. Let
![]() $(x_{\Phi (n)})$
be the sequence constructed in Lemma 7.2 from which we keep the notation. Then:
$(x_{\Phi (n)})$
be the sequence constructed in Lemma 7.2 from which we keep the notation. Then:
-
(a)
 $\sum _{j\in I} \vert z_{j,\Phi (n)}\vert ^2 \to 1$
;
$\sum _{j\in I} \vert z_{j,\Phi (n)}\vert ^2 \to 1$
; -
(b) there exist
 $\#I-1$
elements
$\#I-1$
elements
 $j\in I$
such that
$j\in I$
such that
 $z_{j,\Phi (n)} \to 0$
.
$z_{j,\Phi (n)} \to 0$
.
Proof of Theorem 1.7 by assuming Theorem 8.1
Set
![]() $v_n = \max _{x\in O_\Gamma (y_n)} \{\vert \vert x\vert ^2 -1\vert \}$
. Let
$v_n = \max _{x\in O_\Gamma (y_n)} \{\vert \vert x\vert ^2 -1\vert \}$
. Let
![]() $l\in \mathbb {R}\cup \{+\infty \}$
be an accumulation point of
$l\in \mathbb {R}\cup \{+\infty \}$
be an accumulation point of
![]() $(v_n)$
and show that
$(v_n)$
and show that
![]() $l=0$
, which will finish the proof of our theorem. Without loss of generality, assume that
$l=0$
, which will finish the proof of our theorem. Without loss of generality, assume that
![]() $v_n\to l$
.
$v_n\to l$
.
Pick
![]() $x_n\in O_\Gamma (y_n)$
such that
$x_n\in O_\Gamma (y_n)$
such that
![]() $v_n= \vert \vert x_n\vert ^2 -1 \vert $
. By the preamble of this section, we easily infer that
$v_n= \vert \vert x_n\vert ^2 -1 \vert $
. By the preamble of this section, we easily infer that
![]() $x_n\in l_N(\Gamma )$
for all n and
$x_n\in l_N(\Gamma )$
for all n and
![]() $d_{\Gamma , \varepsilon }(x_n)=d_{\Gamma , \varepsilon }(y_n)\to 1$
for all
$d_{\Gamma , \varepsilon }(x_n)=d_{\Gamma , \varepsilon }(y_n)\to 1$
for all
![]() $\varepsilon>0$
. Thanks to Lemma 7.2
$\varepsilon>0$
. Thanks to Lemma 7.2
![]() $(a)$
, we have
$(a)$
, we have
![]() $x_{\Phi (n)} = \sum _{j\in I} z_{j, \Phi (n)}$
. As a direct consequence of Theorem 8.1, we get
$x_{\Phi (n)} = \sum _{j\in I} z_{j, \Phi (n)}$
. As a direct consequence of Theorem 8.1, we get
![]() $\vert x_{\Phi (n)}\vert ^2\to 1$
. But then
$\vert x_{\Phi (n)}\vert ^2\to 1$
. But then
![]() $v_{\Phi (n)}\to 0$
; whence
$v_{\Phi (n)}\to 0$
; whence
![]() $l=0$
.
$l=0$
.
For the rest of this section, we keep (and fix) the same notation as Theorem 8.1. In order to simplify our explanation, we assume that
![]() $\Phi $
is the identity. Set
$\Phi $
is the identity. Set
![]() $G_n=\mathrm {Gal}(K_\Gamma (\mathcal {F}^{1/(\theta m_n)})/K_\Gamma )$
and
$G_n=\mathrm {Gal}(K_\Gamma (\mathcal {F}^{1/(\theta m_n)})/K_\Gamma )$
and
![]() $H_n=\mathrm {Gal}(K_\Gamma (\mathcal {F}^{1/(\theta m_n)})/K_\Gamma (\mathcal {F}^{1/\theta }))$
. Lemma 2.1 applied to
$H_n=\mathrm {Gal}(K_\Gamma (\mathcal {F}^{1/(\theta m_n)})/K_\Gamma (\mathcal {F}^{1/\theta }))$
. Lemma 2.1 applied to
![]() $m=\infty , d_1=\dots =d_b=\theta m_n$
and
$m=\infty , d_1=\dots =d_b=\theta m_n$
and
![]() $L=\mathbb {Q}(\mathcal {F}^{1/\theta })$
gives
$L=\mathbb {Q}(\mathcal {F}^{1/\theta })$
gives
 $$ \begin{align} H_n= \prod_{l=1}^b \mathbb{Z}/(m_n/c_{l,n})\mathbb{Z}, \end{align} $$
$$ \begin{align} H_n= \prod_{l=1}^b \mathbb{Z}/(m_n/c_{l,n})\mathbb{Z}, \end{align} $$
where
![]() $c_{1,n},\dots , c_{b,n}\in \mathbb {N}$
are bounded from above by a constant depending only on
$c_{1,n},\dots , c_{b,n}\in \mathbb {N}$
are bounded from above by a constant depending only on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\theta $
. Next, for all
$\theta $
. Next, for all
![]() $m\in \mathbb {N}$
, set
$m\in \mathbb {N}$
, set
![]() $. : \mathbb {R}^m \times \mathbb {R}^m \to \mathbb {R}$
to be the dot product on
$. : \mathbb {R}^m \times \mathbb {R}^m \to \mathbb {R}$
to be the dot product on
![]() $\mathbb {R}^m$
. Finally, put
$\mathbb {R}^m$
. Finally, put
![]() $\mathbf {K}_{j,n}=(K_{j,1,n},\dots , K_{j,b,n})$
and for any
$\mathbf {K}_{j,n}=(K_{j,1,n},\dots , K_{j,b,n})$
and for any
![]() $\mathbf {r}=(r_1,\dots ,r_b)\in \mathbb {R}^b$
, we set
$\mathbf {r}=(r_1,\dots ,r_b)\in \mathbb {R}^b$
, we set
 $$\begin{align*}B_{\mathbf{r},i,j,n} = (\overrightarrow{z_{i,n}}, \overrightarrow{z_{j,n}})+ \frac{2\pi \; \mathbf{rc}_n.(\mathbf{K}_{j,n}-\mathbf{K}_{i,n})}{m_n}, \end{align*}$$
$$\begin{align*}B_{\mathbf{r},i,j,n} = (\overrightarrow{z_{i,n}}, \overrightarrow{z_{j,n}})+ \frac{2\pi \; \mathbf{rc}_n.(\mathbf{K}_{j,n}-\mathbf{K}_{i,n})}{m_n}, \end{align*}$$
where
![]() $\mathbf {rc}_n=(r_1c_{1,n}, \dots , r_bc_{b,n})$
.
$\mathbf {rc}_n=(r_1c_{1,n}, \dots , r_bc_{b,n})$
.
8.1 Proof of Theorem 8.1
 $(a)$
$(a)$
We will deduce the limit of Theorem 8.1
![]() $(a)$
thanks to the following equality. Recall that
$(a)$
thanks to the following equality. Recall that
![]() $x_n\in K_\Gamma (\mathcal {F}^{1/(\theta m_n)})$
by Lemma 7.2
$x_n\in K_\Gamma (\mathcal {F}^{1/(\theta m_n)})$
by Lemma 7.2
![]() $(a)$
.
$(a)$
.
Lemma 8.2 Let
![]() $n\in \mathbb {N}$
, and let
$n\in \mathbb {N}$
, and let
![]() $\sigma =\mathbf {r}\in H_n$
. Then
$\sigma =\mathbf {r}\in H_n$
. Then
Proof As
![]() $\sigma \in H_n$
, it therefore fixes the elements of
$\sigma \in H_n$
, it therefore fixes the elements of
![]() $K_\Gamma (\mathcal {F}^{1/\theta })$
. Let
$K_\Gamma (\mathcal {F}^{1/\theta })$
. Let
![]() $j\in I$
. By Lemma 7.2
$j\in I$
. By Lemma 7.2
![]() $(a)$
, we have
$(a)$
, we have
![]() $z_{j,n}=a_{j,n}\prod _{l=1}^b \alpha _l^{K_{j,l,n}/m_n}$
with
$z_{j,n}=a_{j,n}\prod _{l=1}^b \alpha _l^{K_{j,l,n}/m_n}$
with
![]() $a_{j,n}\in K_\Gamma (\mathcal {F}^{1/\theta })$
. A small calculation involving (9) shows that
$a_{j,n}\in K_\Gamma (\mathcal {F}^{1/\theta })$
. A small calculation involving (9) shows that
![]() $\sigma z_{j,n}=z_{j,n} \zeta _{m_n}^{\mathbf {rc}_n.\mathbf {K}_{j,n}}$
. From Lemma 7.2
$\sigma z_{j,n}=z_{j,n} \zeta _{m_n}^{\mathbf {rc}_n.\mathbf {K}_{j,n}}$
. From Lemma 7.2
![]() $(a)$
and from the cosine rule, we get
$(a)$
and from the cosine rule, we get
 $$ \begin{align*} \vert \sigma x_n \vert^2 & = \left\vert \sum_{j\in I} \sigma z_{j,n}\right\vert{}^2 = \left\vert \sum_{j\in I} z_{j,n}\zeta_{m_n}^{\mathbf{rc_n}.\mathbf{K}_{j,n}} \right\vert{}^2 \\ & = \sum_{j\in I} \vert z_{j,n} \vert^2 + \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n}\vert \cos\left( \left(\overrightarrow{ z_{i,n}\zeta_{m_n}^{\mathbf{rc}_n.\mathbf{K}_{i,n}}}, \overrightarrow{ z_{j,n}\zeta_{m_n}^{\mathbf{rc}_n.\mathbf{K}_{j,n}}} \right)\right). \end{align*} $$
$$ \begin{align*} \vert \sigma x_n \vert^2 & = \left\vert \sum_{j\in I} \sigma z_{j,n}\right\vert{}^2 = \left\vert \sum_{j\in I} z_{j,n}\zeta_{m_n}^{\mathbf{rc_n}.\mathbf{K}_{j,n}} \right\vert{}^2 \\ & = \sum_{j\in I} \vert z_{j,n} \vert^2 + \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n}\vert \cos\left( \left(\overrightarrow{ z_{i,n}\zeta_{m_n}^{\mathbf{rc}_n.\mathbf{K}_{i,n}}}, \overrightarrow{ z_{j,n}\zeta_{m_n}^{\mathbf{rc}_n.\mathbf{K}_{j,n}}} \right)\right). \end{align*} $$
To conclude, it remains to show the equality
which is obvious if either
![]() $ z_{i,n}=0$
or
$ z_{i,n}=0$
or
![]() $ z_{j,n}=0$
. If these complex numbers are nonzero, then (10) arises from the chain of equalities modulo
$ z_{j,n}=0$
. If these complex numbers are nonzero, then (10) arises from the chain of equalities modulo
![]() $2\pi $
below
$2\pi $
below
which is valid for all
![]() $\alpha ,\beta \in \mathbb {C}^*$
and all
$\alpha ,\beta \in \mathbb {C}^*$
and all
![]() $\eta ,\lambda \in \mathbb {R}$
.
$\eta ,\lambda \in \mathbb {R}$
.
Fix from now
![]() $\varepsilon>0$
. Let
$\varepsilon>0$
. Let
![]() $F_n$
be the set of elements
$F_n$
be the set of elements
![]() $\sigma \in G_n$
satisfying
$\sigma \in G_n$
satisfying
![]() $1-\varepsilon \leq \vert \sigma x_n\vert ^2 \leq 1+\varepsilon $
. It is easy to check that
$1-\varepsilon \leq \vert \sigma x_n\vert ^2 \leq 1+\varepsilon $
. It is easy to check that
![]() $ d_{\Gamma , \varepsilon }(x_n)=\# F_n/\#G_n$
.
$ d_{\Gamma , \varepsilon }(x_n)=\# F_n/\#G_n$
.
Proof of Theorem 8.1 when I has cardinality
 $1$
$1$
Clearly
![]() $(b)$
arises from
$(b)$
arises from
![]() $(a)$
. Let j be the unique element of I. Lemma 8.2 tells us that
$(a)$
. Let j be the unique element of I. Lemma 8.2 tells us that
![]() $\vert \sigma x_n\vert ^2=\vert z_{j,n}\vert ^2$
for all
$\vert \sigma x_n\vert ^2=\vert z_{j,n}\vert ^2$
for all
![]() $\sigma \in H_n$
. The fact that
$\sigma \in H_n$
. The fact that
![]() $d_{\Gamma , \varepsilon }(x_n)\to 1$
by assumption and that
$d_{\Gamma , \varepsilon }(x_n)\to 1$
by assumption and that
![]() $H_n$
has index
$H_n$
has index
![]() $[K_\Gamma (\mathcal {F}^{1/\theta }) : K_\Gamma ]$
in
$[K_\Gamma (\mathcal {F}^{1/\theta }) : K_\Gamma ]$
in
![]() $G_n$
provides for all n large enough an element
$G_n$
provides for all n large enough an element
![]() $\sigma _n\in H_n$
belonging to
$\sigma _n\in H_n$
belonging to
![]() $F_n$
. In particular,
$F_n$
. In particular,
![]() $1-\varepsilon \leq \vert \sigma _n x_n \vert ^2 = \vert z_{j,n}\vert ^2 \leq 1+\varepsilon $
, and so
$1-\varepsilon \leq \vert \sigma _n x_n \vert ^2 = \vert z_{j,n}\vert ^2 \leq 1+\varepsilon $
, and so
![]() $\vert z_{j,n}\vert ^2\to 1$
proving what we desire.
$\vert z_{j,n}\vert ^2\to 1$
proving what we desire.
We now focus on the case where I has at least two elements.
Lemma 8.2 suggests us to construct for all n large enough a “good”
![]() $\sigma _n=\mathbf {r}_n\in H_n$
for which we can estimate as precisely as possible the quantities
$\sigma _n=\mathbf {r}_n\in H_n$
for which we can estimate as precisely as possible the quantities
![]() $\vert \sigma _n x_n\vert $
and
$\vert \sigma _n x_n\vert $
and
![]() $\cos (B_{\mathbf {r}_n,i,j,n})$
. Its construction is the purpose of the next proposition.
$\cos (B_{\mathbf {r}_n,i,j,n})$
. Its construction is the purpose of the next proposition.
Recall that
![]() $J_l$
is defined in Lemma 7.1. Let Y be the set of pairs
$J_l$
is defined in Lemma 7.1. Let Y be the set of pairs
![]() $(l,m)$
such that
$(l,m)$
such that
![]() $l\in \{1,\dots ,b\}$
and
$l\in \{1,\dots ,b\}$
and
![]() $m\in J_l$
. It is a non-empty set. Indeed, otherwise
$m\in J_l$
. It is a non-empty set. Indeed, otherwise
![]() $J_l$
would be empty for all l. Lemma 7.2 then implies
$J_l$
would be empty for all l. Lemma 7.2 then implies
![]() $K_{j,l,n}=0$
for all
$K_{j,l,n}=0$
for all
![]() $j,l,n$
. But this is possible only if I has cardinality
$j,l,n$
. But this is possible only if I has cardinality
![]() $1$
by Lemma 7.2
$1$
by Lemma 7.2
![]() $(b)$
, a contradiction by the foregoing.
$(b)$
, a contradiction by the foregoing.
Recall that the integer
![]() $\Lambda _m^{(i,l)}$
is defined in Lemma 7.2. Then put
$\Lambda _m^{(i,l)}$
is defined in Lemma 7.2. Then put
 $$\begin{align*}\gamma=\max_{i,j\in I, i\neq j}\left\{\sum_{(l,m)\in Y} \left \vert \Lambda_m^{(j,l)} - \Lambda_m^{(i,l)} \right\vert \right\} +1. \end{align*}$$
$$\begin{align*}\gamma=\max_{i,j\in I, i\neq j}\left\{\sum_{(l,m)\in Y} \left \vert \Lambda_m^{(j,l)} - \Lambda_m^{(i,l)} \right\vert \right\} +1. \end{align*}$$
Let
![]() $i,j\in I$
. Write
$i,j\in I$
. Write
![]() $\boldsymbol {\Lambda }_{i,j}=(\Lambda _m^{(j,l)} - \Lambda _m^{(i,l)})_{(l,m)\in Y}$
. Recall that the sequence
$\boldsymbol {\Lambda }_{i,j}=(\Lambda _m^{(j,l)} - \Lambda _m^{(i,l)})_{(l,m)\in Y}$
. Recall that the sequence
![]() $((\overrightarrow {z_{i,n}}, \overrightarrow {z_{j,n}}))$
converges by Lemma 7.2
$((\overrightarrow {z_{i,n}}, \overrightarrow {z_{j,n}}))$
converges by Lemma 7.2
![]() $(c)$
; denote by
$(c)$
; denote by
![]() $L_{i,j}$
its limit. Finally, for
$L_{i,j}$
its limit. Finally, for
![]() $\mathbf {x}\in \mathbb {R}^{\#Y}$
, we write
$\mathbf {x}\in \mathbb {R}^{\#Y}$
, we write
Proposition 8.3 Let
![]() $\mathbf {x}\in \mathbb {R}^{\#Y}$
. Then, for all n large enough, there exists
$\mathbf {x}\in \mathbb {R}^{\#Y}$
. Then, for all n large enough, there exists
![]() $\sigma _{\mathbf {x}, n}=\mathbf {r}_{\mathbf {x}, n}\in H_n$
such that
$\sigma _{\mathbf {x}, n}=\mathbf {r}_{\mathbf {x}, n}\in H_n$
such that
![]() $ 1-\varepsilon \leq \vert \sigma _{\mathbf {x}, n} x_n \vert ^2 \leq 1+\varepsilon $
. Furthermore, for each
$ 1-\varepsilon \leq \vert \sigma _{\mathbf {x}, n} x_n \vert ^2 \leq 1+\varepsilon $
. Furthermore, for each
![]() $i,j\in I$
distinct such that
$i,j\in I$
distinct such that
![]() $\pm 1\notin I_{i,j}(\mathbf {x})$
, we have
$\pm 1\notin I_{i,j}(\mathbf {x})$
, we have
 $$ \begin{align*} \cos(\gamma\varepsilon)\cos(L_{i,j} + \boldsymbol{\Lambda}_{i,j}.\mathbf{x})+\sin(\gamma\varepsilon) \geq \\ \cos(B_{\mathbf{r}_{\mathbf{x}, n},i,j,n}) \geq \cos(\gamma\varepsilon)\cos(L_{i,j} + \boldsymbol{\Lambda}_{i,j}.\mathbf{x}) - \sin(\gamma\varepsilon). \end{align*} $$
$$ \begin{align*} \cos(\gamma\varepsilon)\cos(L_{i,j} + \boldsymbol{\Lambda}_{i,j}.\mathbf{x})+\sin(\gamma\varepsilon) \geq \\ \cos(B_{\mathbf{r}_{\mathbf{x}, n},i,j,n}) \geq \cos(\gamma\varepsilon)\cos(L_{i,j} + \boldsymbol{\Lambda}_{i,j}.\mathbf{x}) - \sin(\gamma\varepsilon). \end{align*} $$
Proof
First part: As
![]() $d_{\Gamma ,\varepsilon }(x_n)\to 1$
, we deduce that for all n large enough,
$d_{\Gamma ,\varepsilon }(x_n)\to 1$
, we deduce that for all n large enough,
 $$ \begin{align} d_{\Gamma,\varepsilon}(x_n)= \frac{\# F_n}{\# G_n}> 1-\frac{(1-\varepsilon)^b}{2[K_\Gamma(\mathcal{F}^{1/\theta}) : K_\Gamma]} \left(\frac{\varepsilon}{2\pi}\right)^{\sum_{l=1}^b \#J_l}. \end{align} $$
$$ \begin{align} d_{\Gamma,\varepsilon}(x_n)= \frac{\# F_n}{\# G_n}> 1-\frac{(1-\varepsilon)^b}{2[K_\Gamma(\mathcal{F}^{1/\theta}) : K_\Gamma]} \left(\frac{\varepsilon}{2\pi}\right)^{\sum_{l=1}^b \#J_l}. \end{align} $$
Put
![]() $\mathbf {x}=(x_{l,m})_{(l,m)\in Y}$
. For
$\mathbf {x}=(x_{l,m})_{(l,m)\in Y}$
. For
![]() $l\in \{1,\dots ,b\}$
, define
$l\in \{1,\dots ,b\}$
, define
![]() $\mathcal {K}_{l,n}(\mathbf {x})$
to be the set
$\mathcal {K}_{l,n}(\mathbf {x})$
to be the set
![]() $\mathbb {Z}/(m_n/c_{l,n})\mathbb {Z}$
if
$\mathbb {Z}/(m_n/c_{l,n})\mathbb {Z}$
if
![]() $J_l$
is empty and the set of
$J_l$
is empty and the set of
![]() $r\in \mathbb {Z}/(m_n/c_{l,n})\mathbb {Z}$
such that
$r\in \mathbb {Z}/(m_n/c_{l,n})\mathbb {Z}$
such that
if
![]() $J_l$
is non-empty. We have
$J_l$
is non-empty. We have
 $$\begin{align*}\frac{\# \mathcal{K}_{l,n}(\mathbf{x})}{m_n/c_{l,n}}\geq (1-\varepsilon)\left(\frac{\varepsilon}{2\pi}\right)^{\# J_l} \end{align*}$$
$$\begin{align*}\frac{\# \mathcal{K}_{l,n}(\mathbf{x})}{m_n/c_{l,n}}\geq (1-\varepsilon)\left(\frac{\varepsilon}{2\pi}\right)^{\# J_l} \end{align*}$$
for all n large enough. It is clear if
![]() $J_l$
is empty. If not, then by Lemma 7.1
$J_l$
is empty. If not, then by Lemma 7.1
![]() $(a)$
, the sequence of terms
$(a)$
, the sequence of terms
![]() $(\zeta _{m_n}^{k_{m,l,n}})_{m\in J_l}$
is strict. As
$(\zeta _{m_n}^{k_{m,l,n}})_{m\in J_l}$
is strict. As
![]() $c_{l,n}$
is bounded from above by a constant depending only on
$c_{l,n}$
is bounded from above by a constant depending only on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\theta $
, we deduce that the sequence of terms
$\theta $
, we deduce that the sequence of terms
![]() $(\zeta _{m_n/c_{l,n}}^{k_{m,l,n}})_{m\in J_l}$
is also strict. The desired inequality now arises from Corollary 6.2 applied to this sequence,
$(\zeta _{m_n/c_{l,n}}^{k_{m,l,n}})_{m\in J_l}$
is also strict. The desired inequality now arises from Corollary 6.2 applied to this sequence,
![]() $M=\#J_l$
and
$M=\#J_l$
and
![]() $(x_1,\dots ,x_M)=(x_{l,m})_{m\in J_l}$
.
$(x_1,\dots ,x_M)=(x_{l,m})_{m\in J_l}$
.
Clearly,
![]() $\prod _{l=1}^b \mathcal {K}_{l,n}(\mathbf {x})$
is a subset of
$\prod _{l=1}^b \mathcal {K}_{l,n}(\mathbf {x})$
is a subset of
![]() $H_n$
by (9). Moreover,
$H_n$
by (9). Moreover,
![]() $H_n$
has cardinality
$H_n$
has cardinality
![]() $\prod _{l=1}^b m_n/c_{l,n}$
and has index
$\prod _{l=1}^b m_n/c_{l,n}$
and has index
![]() $[K_\Gamma (\mathcal {F}^{1/\theta }) : K_\Gamma ]$
in
$[K_\Gamma (\mathcal {F}^{1/\theta }) : K_\Gamma ]$
in
![]() $G_n$
. Thus
$G_n$
. Thus
 $$ \begin{align*} \frac{\# \prod_{l=1}^b \mathcal{K}_{l,n}(\mathbf{x})}{\#G_n} & = \frac{1}{[K_\Gamma(\mathcal{F}^{1/\theta}) : K_\Gamma]}\prod_{l=1}^b \frac{\# \mathcal{K}_{l,n}(\mathbf{x})}{m_n/c_{l,n}}\geq \frac{(1-\varepsilon)^b }{[K_\Gamma(\mathcal{F}^{1/\theta}) : K_\Gamma]} \left(\frac{\varepsilon}{2\pi}\right)^{\sum_{l=1}^b \#J_l} \end{align*} $$
$$ \begin{align*} \frac{\# \prod_{l=1}^b \mathcal{K}_{l,n}(\mathbf{x})}{\#G_n} & = \frac{1}{[K_\Gamma(\mathcal{F}^{1/\theta}) : K_\Gamma]}\prod_{l=1}^b \frac{\# \mathcal{K}_{l,n}(\mathbf{x})}{m_n/c_{l,n}}\geq \frac{(1-\varepsilon)^b }{[K_\Gamma(\mathcal{F}^{1/\theta}) : K_\Gamma]} \left(\frac{\varepsilon}{2\pi}\right)^{\sum_{l=1}^b \#J_l} \end{align*} $$
for all n large enough. Combining this inequality and (11) provides an element
![]() $\sigma _n =\mathbf {r}=(r_1,\dots ,r_b)\in F_n\cap \prod _{l=1}^b \mathcal {K}_{l,n}(\mathbf {x})$
. This ends the first part.
$\sigma _n =\mathbf {r}=(r_1,\dots ,r_b)\in F_n\cap \prod _{l=1}^b \mathcal {K}_{l,n}(\mathbf {x})$
. This ends the first part.
Second part: Let
![]() $i,j\in I$
be as in the statement. A small calculation gives
$i,j\in I$
be as in the statement. A small calculation gives
 $$ \begin{align*} \zeta_{m_n}^{\mathbf{rc}_n.(\mathbf{K}_{j,n}-\mathbf{K}_{i,n})} & = \zeta_{m_n}^{\sum_{l=1}^b r_lc_{l,n} (K_{j,l,n}-K_{i,l,n})} = \zeta_{m_n}^{\sum_{l=1}^b \sum_{m\in J_l}r_lc_{l,n}(\Lambda_m^{(j,l)} - \Lambda_m^{(i,l)})k_{m,l,n}} \\ & = \prod_{(l,m)\in Y} (\zeta_{m_n}^{ r_lc_{l,n}k_{m,l,n}})^{\Delta_m^{(i,j,l)}}, \end{align*} $$
$$ \begin{align*} \zeta_{m_n}^{\mathbf{rc}_n.(\mathbf{K}_{j,n}-\mathbf{K}_{i,n})} & = \zeta_{m_n}^{\sum_{l=1}^b r_lc_{l,n} (K_{j,l,n}-K_{i,l,n})} = \zeta_{m_n}^{\sum_{l=1}^b \sum_{m\in J_l}r_lc_{l,n}(\Lambda_m^{(j,l)} - \Lambda_m^{(i,l)})k_{m,l,n}} \\ & = \prod_{(l,m)\in Y} (\zeta_{m_n}^{ r_lc_{l,n}k_{m,l,n}})^{\Delta_m^{(i,j,l)}}, \end{align*} $$
where
![]() $\Delta _m^{(i,j,l)}=\Lambda _m^{(j,l)} - \Lambda _m^{(i,l)}\in \mathbb {Z}$
. Let
$\Delta _m^{(i,j,l)}=\Lambda _m^{(j,l)} - \Lambda _m^{(i,l)}\in \mathbb {Z}$
. Let
![]() $(l,m)\in Y$
. In particular,
$(l,m)\in Y$
. In particular,
![]() $J_l$
is non-empty. Recall that
$J_l$
is non-empty. Recall that
![]() $r_l\in \mathcal {K}_{l,n}(\mathbf {x})$
. By definition of
$r_l\in \mathcal {K}_{l,n}(\mathbf {x})$
. By definition of
![]() $\mathcal {K}_{l,n}(\mathbf {x})$
, we have
$\mathcal {K}_{l,n}(\mathbf {x})$
, we have
for all
![]() $m\in J_l$
. Thus
$m\in J_l$
. Thus
 $$ \begin{align*} &\zeta_{m_n}^{\mathbf{rc}_n.(\mathbf{K}_{j,n}-\mathbf{K}_{i,n})} \in \\ &\left[\prod_{(l,m)\in Y} e^{\zeta_4 \left(\Delta_m^{(i,j,l)}x_{l,m} - \varepsilon \left\vert \Delta_m^{(i,j,l)} \right\vert\right)}; \prod_{(l,m)\in Y} e^{\zeta_4\left(\Delta_m^{(i,j,l)} x_{l,m} + \varepsilon \left\vert \Delta_m^{(i,j,l)}\right\vert \right)} \right]. \end{align*} $$
$$ \begin{align*} &\zeta_{m_n}^{\mathbf{rc}_n.(\mathbf{K}_{j,n}-\mathbf{K}_{i,n})} \in \\ &\left[\prod_{(l,m)\in Y} e^{\zeta_4 \left(\Delta_m^{(i,j,l)}x_{l,m} - \varepsilon \left\vert \Delta_m^{(i,j,l)} \right\vert\right)}; \prod_{(l,m)\in Y} e^{\zeta_4\left(\Delta_m^{(i,j,l)} x_{l,m} + \varepsilon \left\vert \Delta_m^{(i,j,l)}\right\vert \right)} \right]. \end{align*} $$
We clearly have
and we finally conclude from the definition of
![]() $\gamma $
that
$\gamma $
that
On the other hand,
![]() $e^{\zeta _4(\overrightarrow {z_{i,n}}, \overrightarrow {z_{j,n}})}\in [e^{\zeta _4(L_{i,j}-\varepsilon )},e^{\zeta _4( L_{i,j}+\varepsilon )}]$
for all n large enough since
$e^{\zeta _4(\overrightarrow {z_{i,n}}, \overrightarrow {z_{j,n}})}\in [e^{\zeta _4(L_{i,j}-\varepsilon )},e^{\zeta _4( L_{i,j}+\varepsilon )}]$
for all n large enough since
![]() $(\overrightarrow {z_{i,n}}, \overrightarrow {z_{j,n}}) \to L_{i,j}$
. From all this, we conclude that for all n large enough,
$(\overrightarrow {z_{i,n}}, \overrightarrow {z_{j,n}}) \to L_{i,j}$
. From all this, we conclude that for all n large enough,
By assumption,
![]() $\pm 1 \notin I_{i,j}(\mathbf {x})$
. The real part function is therefore monotone on
$\pm 1 \notin I_{i,j}(\mathbf {x})$
. The real part function is therefore monotone on
![]() $I_{i,j}(\mathbf {x})$
. In particular, it reaches its extrema to the two endpoints of
$I_{i,j}(\mathbf {x})$
. In particular, it reaches its extrema to the two endpoints of
![]() $I_{i,j}(\mathbf {x})$
. If it is decreasing, then
$I_{i,j}(\mathbf {x})$
. If it is decreasing, then
We deduce the desired inequality thanks to the relations
![]() $\cos (x-y)=\cos (x)\cos (y)+\sin (x)\sin (y)$
,
$\cos (x-y)=\cos (x)\cos (y)+\sin (x)\sin (y)$
,
![]() $\cos (x+y) = \cos (x)\cos (y)- \sin (x)\sin (y),$
and
$\cos (x+y) = \cos (x)\cos (y)- \sin (x)\sin (y),$
and
![]() $\vert \sin (x)\vert \leq 1$
. The increasing case is similar, which proves the second part of the statement.
$\vert \sin (x)\vert \leq 1$
. The increasing case is similar, which proves the second part of the statement.
The key to get Theorem 8.1
![]() $(a)$
is to apply the previous proposition to a finite number of well-chosen
$(a)$
is to apply the previous proposition to a finite number of well-chosen
![]() $\mathbf {x}$
. But before constructing them, we need some preliminary results.
$\mathbf {x}$
. But before constructing them, we need some preliminary results.
Lemma 8.4 Let
![]() $i,j\in I$
be distinct. Then
$i,j\in I$
be distinct. Then
![]() $\boldsymbol {\Lambda }_{i,j}$
is nonzero.
$\boldsymbol {\Lambda }_{i,j}$
is nonzero.
Proof If
![]() $\boldsymbol {\Lambda }_{i,j}$
is zero, then
$\boldsymbol {\Lambda }_{i,j}$
is zero, then
![]() $\Lambda _m^{(j,l)}=\Lambda _m^{(i,l)}$
for all
$\Lambda _m^{(j,l)}=\Lambda _m^{(i,l)}$
for all
![]() $(l,m)\in Y$
, i.e., for all
$(l,m)\in Y$
, i.e., for all
![]() $l\in \{1,\dots ,b\}$
and all
$l\in \{1,\dots ,b\}$
and all
![]() $m\in J_l$
. But then, Lemma 7.2 implies
$m\in J_l$
. But then, Lemma 7.2 implies
![]() $K_{i,l,n}=K_{j,l,n}$
for all
$K_{i,l,n}=K_{j,l,n}$
for all
![]() $l\in \{1,\dots ,b\}$
and all n, i.e.,
$l\in \{1,\dots ,b\}$
and all n, i.e.,
![]() $(K_{i,1,n},\dots ,K_{i,b,n})=(K_{j,1,n},\dots , K_{j,b,n})$
for all n. This is possible only if
$(K_{i,1,n},\dots ,K_{i,b,n})=(K_{j,1,n},\dots , K_{j,b,n})$
for all n. This is possible only if
![]() $i=j$
according to Lemma 7.2
$i=j$
according to Lemma 7.2
![]() $(b)$
, a contradiction. The lemma follows.
$(b)$
, a contradiction. The lemma follows.
We can thus fix an integer
![]() $d\in \mathbb {N}$
such that for all
$d\in \mathbb {N}$
such that for all
![]() $i,j\in I$
distinct, d does not divide at least one of the coordinates of
$i,j\in I$
distinct, d does not divide at least one of the coordinates of
![]() $\boldsymbol {\Lambda }_{i,j}$
. Put
$\boldsymbol {\Lambda }_{i,j}$
. Put
Lemma 8.5 Let
![]() $i,j\in I$
be distinct. Then
$i,j\in I$
be distinct. Then
![]() $\sum _{\mathbf {z}\in Z} e^{\zeta _4 \boldsymbol {\Lambda }_{i,j}.\mathbf {z}}=0$
.
$\sum _{\mathbf {z}\in Z} e^{\zeta _4 \boldsymbol {\Lambda }_{i,j}.\mathbf {z}}=0$
.
Proof For brevity, write
![]() $\boldsymbol {\Lambda }_{i,j}=(\lambda _1,\dots , \lambda _{\#Y})$
. Thus
$\boldsymbol {\Lambda }_{i,j}=(\lambda _1,\dots , \lambda _{\#Y})$
. Thus
By definition of d, there is
![]() $u\in \{1,\dots ,\# Y\}$
such that d does not divide
$u\in \{1,\dots ,\# Y\}$
such that d does not divide
![]() $\lambda _u$
. So
$\lambda _u$
. So
 $$\begin{align*}\sum_{\mathbf{z}\in Z} e^{\zeta_4 \boldsymbol{\Lambda}_{i,j}.\mathbf{z}} = \sum_{0\leq k_1,\dots, k_{u-1}, k_{u+1}, \dots, k_{\#Y}\leq d-1} \zeta_d^{\sum_{\underset{t\neq u}{t=1}}^{\#Y} \lambda_t k_t} \sum_{k_u=0}^{d-1} \zeta_d^{\lambda_u k_u}. \end{align*}$$
$$\begin{align*}\sum_{\mathbf{z}\in Z} e^{\zeta_4 \boldsymbol{\Lambda}_{i,j}.\mathbf{z}} = \sum_{0\leq k_1,\dots, k_{u-1}, k_{u+1}, \dots, k_{\#Y}\leq d-1} \zeta_d^{\sum_{\underset{t\neq u}{t=1}}^{\#Y} \lambda_t k_t} \sum_{k_u=0}^{d-1} \zeta_d^{\lambda_u k_u}. \end{align*}$$
Finally,
![]() $\sum _{k=0}^{d-1} \zeta _d^{\lambda _u k}=0$
since d does not divide
$\sum _{k=0}^{d-1} \zeta _d^{\lambda _u k}=0$
since d does not divide
![]() $\lambda _u$
. The lemma follows.
$\lambda _u$
. The lemma follows.
We would like to apply Proposition 8.3 for all
![]() $\mathbf {x}\in Z$
. However, there is no guarantee that the condition
$\mathbf {x}\in Z$
. However, there is no guarantee that the condition
![]() $\pm 1\notin I_{i,j}(\mathbf {x})$
holds for all
$\pm 1\notin I_{i,j}(\mathbf {x})$
holds for all
![]() $i,j\in I$
distinct and all
$i,j\in I$
distinct and all
![]() $\mathbf {x}\in Z$
. We see below how to circumvent this difficulty.
$\mathbf {x}\in Z$
. We see below how to circumvent this difficulty.
We define
![]() $\mathcal {H}$
to be the set of
$\mathcal {H}$
to be the set of
![]() $\mathbf {X} \in [0;2\pi ]^{\# Y}$
satisfying
$\mathbf {X} \in [0;2\pi ]^{\# Y}$
satisfying
As
![]() $\boldsymbol {\Lambda }_{i,j}$
is nonzero for all
$\boldsymbol {\Lambda }_{i,j}$
is nonzero for all
![]() $i,j\in I$
distinct, we infer that
$i,j\in I$
distinct, we infer that
![]() $\mathcal {H}$
lies in a finite union of hyperplanes in
$\mathcal {H}$
lies in a finite union of hyperplanes in
![]() $\mathbb {R}^{\#Y}$
(the equation above having no solution if
$\mathbb {R}^{\#Y}$
(the equation above having no solution if
![]() $\vert t \vert $
is large enough since the quantity
$\vert t \vert $
is large enough since the quantity
![]() $\mathbf {X}$
is bounded). Hence, there exists a simply-connected compact
$\mathbf {X}$
is bounded). Hence, there exists a simply-connected compact
![]() $K \subset [0;2\pi ]^{\#Y}$
such that
$K \subset [0;2\pi ]^{\#Y}$
such that
![]() $K \cap \mathcal {H}$
is empty. The distance
$K \cap \mathcal {H}$
is empty. The distance
![]() $\delta $
from K to
$\delta $
from K to
![]() $\mathcal {H}$
is a positive real since both K and
$\mathcal {H}$
is a positive real since both K and
![]() $\mathcal {H}$
are compact. For
$\mathcal {H}$
are compact. For
![]() $\mathbf {x}_0\in K$
, the distance from
$\mathbf {x}_0\in K$
, the distance from
![]() $\mathbf {x}_0$
to
$\mathbf {x}_0$
to
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
 $$\begin{align*}\min_{t\in \mathbb{Z}, i\neq j\in I, \mathbf{z}\in Z}\left\{ \frac{\vert L_{i,j}+ \boldsymbol{\Lambda}_{i,j}.(\mathbf{x}_0+\mathbf{z}) - t\pi \vert}{\sqrt{\boldsymbol{\Lambda}_{i,j}.\boldsymbol{\Lambda}_{i,j}}}\right\}\geq \delta. \end{align*}$$
$$\begin{align*}\min_{t\in \mathbb{Z}, i\neq j\in I, \mathbf{z}\in Z}\left\{ \frac{\vert L_{i,j}+ \boldsymbol{\Lambda}_{i,j}.(\mathbf{x}_0+\mathbf{z}) - t\pi \vert}{\sqrt{\boldsymbol{\Lambda}_{i,j}.\boldsymbol{\Lambda}_{i,j}}}\right\}\geq \delta. \end{align*}$$
As
![]() $\boldsymbol {\Lambda }_{i,j}\in \mathbb {Z}^{\#Y}$
is nonzero, we conclude
$\boldsymbol {\Lambda }_{i,j}\in \mathbb {Z}^{\#Y}$
is nonzero, we conclude
![]() $\sqrt {\boldsymbol {\Lambda }_{i,j}.\boldsymbol {\Lambda }_{i,j}}\geq 1$
, and so
$\sqrt {\boldsymbol {\Lambda }_{i,j}.\boldsymbol {\Lambda }_{i,j}}\geq 1$
, and so
for all
![]() $t\in \mathbb {Z}$
, all
$t\in \mathbb {Z}$
, all
![]() $i,j\in I$
distinct and all
$i,j\in I$
distinct and all
![]() $\mathbf {x}\in K+Z= \{ \mathbf {X}+\mathbf {z}, \mathbf {X}\in K, \mathbf {z}\in Z\}$
.
$\mathbf {x}\in K+Z= \{ \mathbf {X}+\mathbf {z}, \mathbf {X}\in K, \mathbf {z}\in Z\}$
.
Recall that
![]() $\varepsilon $
is as small as possible. So we can take it such that
$\varepsilon $
is as small as possible. So we can take it such that
![]() $\gamma \varepsilon < \delta $
. Thus
$\gamma \varepsilon < \delta $
. Thus
for all
![]() $t\in \mathbb {Z}$
, all
$t\in \mathbb {Z}$
, all
![]() $i,j\in I$
distinct and all
$i,j\in I$
distinct and all
![]() $\mathbf {x}\in K+Z$
. In conclusion,
$\mathbf {x}\in K+Z$
. In conclusion,
![]() $\pm 1\notin I_{i,j}(\mathbf {x})$
for all
$\pm 1\notin I_{i,j}(\mathbf {x})$
for all
![]() $i,j\in I$
distinct and all
$i,j\in I$
distinct and all
![]() $\mathbf {x}\in K+Z$
.
$\mathbf {x}\in K+Z$
.
Here is the last calculation before starting the proof of Theorem 8.1
![]() $(a)$
.
$(a)$
.
Lemma 8.6 Let
![]() $\eta , x_j\in \mathbb {C}$
be complex numbers with
$\eta , x_j\in \mathbb {C}$
be complex numbers with
![]() $j\in I$
. Then
$j\in I$
. Then
Proof For brevity, put
![]() $\eta _1=-\eta /2$
and
$\eta _1=-\eta /2$
and
![]() $\eta _2=1+\eta (\#I-1)$
. Then
$\eta _2=1+\eta (\#I-1)$
. Then
 $$ \begin{align*} \eta_1\sum_{i,j\in I, i\neq j} (x_i-x_j)^2 + \eta_2\sum_{j\in I} x_j^2 & = \eta_1\sum_{i,j\in I, i\neq j} (x_i^2+x_j^2-2x_ix_j) +\eta_2\sum_{j\in I} x_j^2 \\ & = 2(\#I-1)\eta_1\sum_{i\in I} x_i^2 -2\eta_1\sum_{i,j\in I, i\neq j} x_ix_j +\eta_2 \sum_{j\in I} x_j^2 \\ & = (\eta_2+2(\#I-1)\eta_1) \sum_{j\in I} x_j^2 -2\eta_1\sum_{i,j\in I, i\neq j} x_ix_j, \end{align*} $$
$$ \begin{align*} \eta_1\sum_{i,j\in I, i\neq j} (x_i-x_j)^2 + \eta_2\sum_{j\in I} x_j^2 & = \eta_1\sum_{i,j\in I, i\neq j} (x_i^2+x_j^2-2x_ix_j) +\eta_2\sum_{j\in I} x_j^2 \\ & = 2(\#I-1)\eta_1\sum_{i\in I} x_i^2 -2\eta_1\sum_{i,j\in I, i\neq j} x_ix_j +\eta_2 \sum_{j\in I} x_j^2 \\ & = (\eta_2+2(\#I-1)\eta_1) \sum_{j\in I} x_j^2 -2\eta_1\sum_{i,j\in I, i\neq j} x_ix_j, \end{align*} $$
and the lemma follows since
![]() $-2\eta _1=\eta $
and
$-2\eta _1=\eta $
and
![]() $\eta _2+2(\#I-1)\eta _1=1$
.
$\eta _2+2(\#I-1)\eta _1=1$
.
Proof of Theorem 8.1
 $(a)$
$(a)$
Let
![]() $\mathbf {y}\in K$
. Recall that
$\mathbf {y}\in K$
. Recall that
![]() $\pm 1 \notin I_{i,j}(\mathbf {x})$
for all
$\pm 1 \notin I_{i,j}(\mathbf {x})$
for all
![]() $i,j\in I$
distinct and all
$i,j\in I$
distinct and all
![]() $\mathbf {x}\in \mathbf {y}+Z$
. The set
$\mathbf {x}\in \mathbf {y}+Z$
. The set
![]() $\mathbf {y}+Z$
being finite, we infer that for all n large enough, Proposition 8.3 holds for all elements
$\mathbf {y}+Z$
being finite, we infer that for all n large enough, Proposition 8.3 holds for all elements
![]() $\mathbf {x}\in \mathbf {y}+Z$
. Choose such a n.
$\mathbf {x}\in \mathbf {y}+Z$
. Choose such a n.
Lemma 8.5 easily implies
![]() $\sum _{\mathbf {x}\in \mathbf {y}+Z} \cos (L_{i,j}+ \mathbf {\Lambda }_{i.j}.\mathbf {x})=0$
for all
$\sum _{\mathbf {x}\in \mathbf {y}+Z} \cos (L_{i,j}+ \mathbf {\Lambda }_{i.j}.\mathbf {x})=0$
for all
![]() $i,j\in I$
distinct. Summing over
$i,j\in I$
distinct. Summing over
![]() $\mathbf {y}+Z$
the chain of inequalities in Proposition 8.3 leads to
$\mathbf {y}+Z$
the chain of inequalities in Proposition 8.3 leads to
Proposition 8.3 gives
![]() $1+\varepsilon \geq \vert \sigma _{\mathbf {x}, n} x_n\vert ^2 \geq 1-\varepsilon $
for all
$1+\varepsilon \geq \vert \sigma _{\mathbf {x}, n} x_n\vert ^2 \geq 1-\varepsilon $
for all
![]() $\mathbf {x}\in \mathbf {y}+ Z$
. By Lemma 8.2,
$\mathbf {x}\in \mathbf {y}+ Z$
. By Lemma 8.2,
By summing these inequalities over
![]() $\mathbf {y}+Z$
, we conclude
$\mathbf {y}+Z$
, we conclude
and
Finally, Lemma 8.6 applied to
![]() $x_j=\vert z_{j,n}\vert $
and
$x_j=\vert z_{j,n}\vert $
and
![]() $\eta =\pm \sin (\gamma \varepsilon )$
gives us
$\eta =\pm \sin (\gamma \varepsilon )$
gives us
 $$ \begin{align*} 1+\varepsilon & \geq \frac{\sin(\gamma\varepsilon)}{2}\sum_{i,j\in I, i\neq j}(\vert z_{i,n}\vert - \vert z_{j,n} \vert)^2 + \left(1-(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2 \\ &\geq \left(1-(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2 \end{align*} $$
$$ \begin{align*} 1+\varepsilon & \geq \frac{\sin(\gamma\varepsilon)}{2}\sum_{i,j\in I, i\neq j}(\vert z_{i,n}\vert - \vert z_{j,n} \vert)^2 + \left(1-(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2 \\ &\geq \left(1-(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2 \end{align*} $$
and
 $$ \begin{align*} 1-\varepsilon & \leq -\frac{\sin(\gamma\varepsilon)}{2}\sum_{i,j\in I, i\neq j}(\vert z_{i,n}\vert - \vert z_{j,n} \vert)^2 + \left(1+(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2 \\ & \leq \left(1+(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2. \end{align*} $$
$$ \begin{align*} 1-\varepsilon & \leq -\frac{\sin(\gamma\varepsilon)}{2}\sum_{i,j\in I, i\neq j}(\vert z_{i,n}\vert - \vert z_{j,n} \vert)^2 + \left(1+(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2 \\ & \leq \left(1+(\#I-1)\sin(\gamma\varepsilon)\right)\sum_{j\in I} \vert z_{j,n}\vert^2. \end{align*} $$
In conclusion, for all n large enough, we have
 $$\begin{align*}\frac{1-\varepsilon}{1+(\#I-1)\sin(\gamma\varepsilon)} \leq \sum_{j\in I} \vert z_{j,n}\vert^2 \leq \frac{1+\varepsilon}{1-(\#I-1)\sin(\gamma\varepsilon)}, \end{align*}$$
$$\begin{align*}\frac{1-\varepsilon}{1+(\#I-1)\sin(\gamma\varepsilon)} \leq \sum_{j\in I} \vert z_{j,n}\vert^2 \leq \frac{1+\varepsilon}{1-(\#I-1)\sin(\gamma\varepsilon)}, \end{align*}$$
i.e.,
![]() $\sum _{j\in I} \vert z_{j,n}\vert ^2 \to 1$
, which proves Theorem 8.1
$\sum _{j\in I} \vert z_{j,n}\vert ^2 \to 1$
, which proves Theorem 8.1
![]() $(a)$
.
$(a)$
.
8.2 Proof of Theorem 8.1
 $(b)$
$(b)$
Recall that
![]() $\pm 1 \notin I_{i,j}(\mathbf {x})$
for all
$\pm 1 \notin I_{i,j}(\mathbf {x})$
for all
![]() $i,j\in I$
distinct and all
$i,j\in I$
distinct and all
![]() $\mathbf {x}\in K\subset K+Z$
. We can now show the pointwise limit below.
$\mathbf {x}\in K\subset K+Z$
. We can now show the pointwise limit below.
Lemma 8.7 Pick
![]() $\mathbf {x}\in K$
. Then
$\mathbf {x}\in K$
. Then
![]() $\sum _{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n} \vert \cos \left ( L_{i,j} + \boldsymbol {\Lambda }_{i,j}.\mathbf {x} \right ) \to 0$
.
$\sum _{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n} \vert \cos \left ( L_{i,j} + \boldsymbol {\Lambda }_{i,j}.\mathbf {x} \right ) \to 0$
.
Proof Thanks to Theorem 8.1
![]() $(a)$
, we have
$(a)$
, we have
![]() $1-\varepsilon \leq \sum _{j\in I} \vert z_{j,n} \vert ^2 \leq 1+\varepsilon $
for all n large enough. Furthermore, for all n large enough, there is
$1-\varepsilon \leq \sum _{j\in I} \vert z_{j,n} \vert ^2 \leq 1+\varepsilon $
for all n large enough. Furthermore, for all n large enough, there is
![]() $\sigma _{\mathbf {x},n}\in H_n$
as in Proposition 8.3. Choose n large enough so that the facts above hold.
$\sigma _{\mathbf {x},n}\in H_n$
as in Proposition 8.3. Choose n large enough so that the facts above hold.
Using the triangle inequality, then Proposition 8.3, we get
 $$ \begin{align} \left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \left(\cos (B_{\mathbf{r_{\mathbf{x},n}},i,j,n}) -\cos(\gamma\varepsilon) \cos\left(L_{i,j}+\boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right)\right) \right\vert \leq \\ \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n}\vert \sin(\gamma\epsilon)\leq \gamma\varepsilon \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert. \nonumber \end{align} $$
$$ \begin{align} \left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \left(\cos (B_{\mathbf{r_{\mathbf{x},n}},i,j,n}) -\cos(\gamma\varepsilon) \cos\left(L_{i,j}+\boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right)\right) \right\vert \leq \\ \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n}\vert \sin(\gamma\epsilon)\leq \gamma\varepsilon \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert. \nonumber \end{align} $$
We also have
![]() $1-\varepsilon \leq \vert \sigma _{\mathbf {x},n} x_n\vert ^2 \leq 1+\varepsilon $
by Proposition 8.3. Recall that we have the chain of inequalities
$1-\varepsilon \leq \vert \sigma _{\mathbf {x},n} x_n\vert ^2 \leq 1+\varepsilon $
by Proposition 8.3. Recall that we have the chain of inequalities
![]() $1-\varepsilon \leq \sum _{j\in I} \vert z_{j,n} \vert ^2 \leq 1+\varepsilon $
. Thanks to Lemma 8.2, we obtain
$1-\varepsilon \leq \sum _{j\in I} \vert z_{j,n} \vert ^2 \leq 1+\varepsilon $
. Thanks to Lemma 8.2, we obtain
 $$ \begin{align} \left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \cos (B_{\mathbf{r}_{\mathbf{x},n},i,j,n}) \right\vert \leq 2\varepsilon. \end{align} $$
$$ \begin{align} \left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \cos (B_{\mathbf{r}_{\mathbf{x},n},i,j,n}) \right\vert \leq 2\varepsilon. \end{align} $$
Applying the reverse triangle inequality to (12), it follows from (13) that
 $$\begin{align*}\cos(\gamma\varepsilon) \left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \cos\left(L_{i,j}+\boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right) \right\vert \leq \varepsilon\left(\gamma \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert +2 \right). \end{align*}$$
$$\begin{align*}\cos(\gamma\varepsilon) \left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \cos\left(L_{i,j}+\boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right) \right\vert \leq \varepsilon\left(\gamma \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert +2 \right). \end{align*}$$
As
![]() $\vert z_{j,n} \vert ^2\leq 1+\varepsilon $
for all
$\vert z_{j,n} \vert ^2\leq 1+\varepsilon $
for all
![]() $j\in I$
, we finally conclude that for all n large enough,
$j\in I$
, we finally conclude that for all n large enough,
 $$\begin{align*}\left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \cos\left(L_{i,j}+\boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right) \right\vert \leq \frac{\varepsilon}{\cos(\gamma\varepsilon)} (2+\gamma(1+\varepsilon) (\# I)^2) ,\end{align*}$$
$$\begin{align*}\left\vert \sum_{i,j\in I, i\neq j} \vert z_{i,n} \vert \vert z_{j,n } \vert \cos\left(L_{i,j}+\boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right) \right\vert \leq \frac{\varepsilon}{\cos(\gamma\varepsilon)} (2+\gamma(1+\varepsilon) (\# I)^2) ,\end{align*}$$
which ends the proof of the lemma.
Let
![]() $\{\mathbf {c}_1,\dots , \mathbf {c}_M\}=\{\boldsymbol {\Lambda }_{i,j}, i, j\in I, i\neq j\}$
be with
$\{\mathbf {c}_1,\dots , \mathbf {c}_M\}=\{\boldsymbol {\Lambda }_{i,j}, i, j\in I, i\neq j\}$
be with
![]() $\mathbf {c}_1,\dots ,\mathbf {c}_M$
pairwise distinct. For
$\mathbf {c}_1,\dots ,\mathbf {c}_M$
pairwise distinct. For
![]() $k\in \{1,\dots , M\}$
, put
$k\in \{1,\dots , M\}$
, put
![]() $E_k$
the set of
$E_k$
the set of
![]() $i,j\in I$
distinct such that
$i,j\in I$
distinct such that
![]() $\mathbf {c}_k=\boldsymbol {\Lambda }_{i,j}$
. Clearly,
$\mathbf {c}_k=\boldsymbol {\Lambda }_{i,j}$
. Clearly,
![]() $E_1,\dots , E_k$
is a partition of
$E_1,\dots , E_k$
is a partition of
![]() $I^2\backslash \bigsqcup _{l\in I} (l,l)$
.
$I^2\backslash \bigsqcup _{l\in I} (l,l)$
.
We now state a much more precise result than Lemma 8.7.
Lemma 8.8 We have
![]() $\sum _{(i,j)\in E_k} \vert z_{i,n}\vert \vert z_{j,n}\vert e^{\zeta _4 L_{i,j} } \to 0$
for all
$\sum _{(i,j)\in E_k} \vert z_{i,n}\vert \vert z_{j,n}\vert e^{\zeta _4 L_{i,j} } \to 0$
for all
![]() $k\in \{1,\dots ,M\}$
.
$k\in \{1,\dots ,M\}$
.
Proof Write
The sequence of terms
![]() $(C_{k,n}, S_{k,n})_{k=1}^M$
has an accumulation point in
$(C_{k,n}, S_{k,n})_{k=1}^M$
has an accumulation point in
![]() $\mathbb {R}^{2M}$
since it is bounded by Theorem 8.1
$\mathbb {R}^{2M}$
since it is bounded by Theorem 8.1
![]() $(a)$
. Let
$(a)$
. Let
![]() $(C_k,S_k)_{k=1}^M$
be such a point. To show our lemma, it is sufficient to get
$(C_k,S_k)_{k=1}^M$
be such a point. To show our lemma, it is sufficient to get
![]() $C_k=S_k=0$
for all
$C_k=S_k=0$
for all
![]() $k\in \{1,\dots ,M\}$
. Without loss of generality, assume that
$k\in \{1,\dots ,M\}$
. Without loss of generality, assume that
![]() $(C_{k,n}, S_{k,n})_{k=1}^M\to (C_k, S_k)_{k=1}^M$
.
$(C_{k,n}, S_{k,n})_{k=1}^M\to (C_k, S_k)_{k=1}^M$
.
Let
![]() $\mathbf {x}\in K$
. A short calculation gives
$\mathbf {x}\in K$
. A short calculation gives
 $$ \begin{align*} \sum_{i,j\in I, i\neq j} \vert z_{i,n}\vert \vert z_{j,n}\vert \cos\left(L_{i,j}+ \boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right) & = \sum_{k=1}^M \sum_{(i,j)\in E_k} \vert z_{i,n}\vert \vert z_{j,n}\vert \cos\left(L_{i,j}+ \mathbf{c}_k.\mathbf{x} \right) \\ & = \sum_{k=1}^M C_{k,n}\cos\left( \mathbf{c}_k.\mathbf{x}\right) + S_{k,n}\sin\left(\mathbf{c}_k.\mathbf{x} \right). \end{align*} $$
$$ \begin{align*} \sum_{i,j\in I, i\neq j} \vert z_{i,n}\vert \vert z_{j,n}\vert \cos\left(L_{i,j}+ \boldsymbol{\Lambda}_{i,j}.\mathbf{x}\right) & = \sum_{k=1}^M \sum_{(i,j)\in E_k} \vert z_{i,n}\vert \vert z_{j,n}\vert \cos\left(L_{i,j}+ \mathbf{c}_k.\mathbf{x} \right) \\ & = \sum_{k=1}^M C_{k,n}\cos\left( \mathbf{c}_k.\mathbf{x}\right) + S_{k,n}\sin\left(\mathbf{c}_k.\mathbf{x} \right). \end{align*} $$
We deduce from Lemma 8.7 that
![]() $\sum _{k=1}^M C_{k,n}\cos \left ( \mathbf {c}_k.\mathbf {x}\right ) + S_{k,n}\sin \left (\mathbf {c}_k.\mathbf {x} \right ) \to 0$
and the uniqueness of the limit gives
$\sum _{k=1}^M C_{k,n}\cos \left ( \mathbf {c}_k.\mathbf {x}\right ) + S_{k,n}\sin \left (\mathbf {c}_k.\mathbf {x} \right ) \to 0$
and the uniqueness of the limit gives
 $$\begin{align*}\sum_{k=1}^M C_k \cos\left( \mathbf{c}_k.\mathbf{x} \right) + S_k \sin\left(\mathbf{c}_k.\mathbf{x} \right) =0.\end{align*}$$
$$\begin{align*}\sum_{k=1}^M C_k \cos\left( \mathbf{c}_k.\mathbf{x} \right) + S_k \sin\left(\mathbf{c}_k.\mathbf{x} \right) =0.\end{align*}$$
As K is a simply-connected compact, the Monodromy Theorem claims that this equality holds for all
![]() $\mathbf {x}\in \mathbb {C}^{\#Y}$
. Thus, for such a
$\mathbf {x}\in \mathbb {C}^{\#Y}$
. Thus, for such a
![]() $\mathbf {x}$
, we have
$\mathbf {x}$
, we have
 $$\begin{align*}\sum_{k=1}^M C_k\cos\left( \mathbf{c}_k.\mathbf{x}\right)= \sum_{k=1}^M S_k\sin\left( \mathbf{c}_k.\mathbf{x}\right)=0,\end{align*}$$
$$\begin{align*}\sum_{k=1}^M C_k\cos\left( \mathbf{c}_k.\mathbf{x}\right)= \sum_{k=1}^M S_k\sin\left( \mathbf{c}_k.\mathbf{x}\right)=0,\end{align*}$$
since the functions
![]() $\mathbf {x}\mapsto \sum _{k=1}^M C_k\cos \left ( \mathbf {c}_k.\mathbf {x}\right )$
and
$\mathbf {x}\mapsto \sum _{k=1}^M C_k\cos \left ( \mathbf {c}_k.\mathbf {x}\right )$
and
![]() $\mathbf {x}\mapsto \sum _{k=1}^M S_k\sin \left ( \mathbf {c}_k.\mathbf {x}\right )$
are both even and odd. The tuples
$\mathbf {x}\mapsto \sum _{k=1}^M S_k\sin \left ( \mathbf {c}_k.\mathbf {x}\right )$
are both even and odd. The tuples
![]() $\mathbf {c}_1, \dots , \mathbf {c}_M$
being pairwise distinct by construction, we get
$\mathbf {c}_1, \dots , \mathbf {c}_M$
being pairwise distinct by construction, we get
![]() $C_k=S_k=0$
for all
$C_k=S_k=0$
for all
![]() $k\in \{1,\dots ,M\}$
. The lemma follows.
$k\in \{1,\dots ,M\}$
. The lemma follows.
For all
![]() $i,j\in I$
, put
$i,j\in I$
, put
![]() $\boldsymbol {\Lambda }_j=(\Lambda _m^{(j,l)})_{(l,m)\in Y}$
and note that
$\boldsymbol {\Lambda }_j=(\Lambda _m^{(j,l)})_{(l,m)\in Y}$
and note that
![]() $\boldsymbol {\Lambda }_{i,j}=\boldsymbol {\Lambda }_j-\boldsymbol {\Lambda }_i$
. Thanks to Lemma 8.4, it follows that
$\boldsymbol {\Lambda }_{i,j}=\boldsymbol {\Lambda }_j-\boldsymbol {\Lambda }_i$
. Thanks to Lemma 8.4, it follows that
![]() $\boldsymbol {\Lambda }_j$
are pairwise distinct when j runs over all elements of I. We now compare these tuples as follows: We say that
$\boldsymbol {\Lambda }_j$
are pairwise distinct when j runs over all elements of I. We now compare these tuples as follows: We say that
![]() $\boldsymbol {\Lambda }_i$
is less than
$\boldsymbol {\Lambda }_i$
is less than
![]() $\boldsymbol {\Lambda }_j$
if and only if
$\boldsymbol {\Lambda }_j$
if and only if
![]() $\Lambda _m^{(i,l)} < \Lambda _m^{(j,l)}$
, where
$\Lambda _m^{(i,l)} < \Lambda _m^{(j,l)}$
, where
![]() $(l,m)$
is the smallest element of Y (for the usual lexicographic order in
$(l,m)$
is the smallest element of Y (for the usual lexicographic order in
![]() $\mathbb {R}^2$
) for which
$\mathbb {R}^2$
) for which
![]() $\Lambda _m^{(i,l)}$
and
$\Lambda _m^{(i,l)}$
and
![]() $\Lambda _m^{(j,l)}$
differ.
$\Lambda _m^{(j,l)}$
differ.
Proof of Theorem 8.1
 $(b)$
$(b)$
Write E for the set of elements
![]() $j\in I$
such that the sequence
$j\in I$
such that the sequence
![]() $(z_{j,n})$
does not go to
$(z_{j,n})$
does not go to
![]() $0$
. Theorem 8.1
$0$
. Theorem 8.1
![]() $(a)$
claims that E is non-empty. To get
$(a)$
claims that E is non-empty. To get
![]() $(b)$
, it suffices to prove that
$(b)$
, it suffices to prove that
![]() $\#E=1$
. Assume by contradiction that
$\#E=1$
. Assume by contradiction that
![]() $\# E>1$
. Let
$\# E>1$
. Let
![]() $i_0, j_0\in E$
be distinct such that
$i_0, j_0\in E$
be distinct such that
![]() $\boldsymbol {\Lambda }_{j_0}=\max _{h\in E} \boldsymbol {\Lambda }_h$
and
$\boldsymbol {\Lambda }_{j_0}=\max _{h\in E} \boldsymbol {\Lambda }_h$
and
![]() $\boldsymbol {\Lambda }_{i_0}=\min _{h\in E} \boldsymbol {\Lambda }_h$
.
$\boldsymbol {\Lambda }_{i_0}=\min _{h\in E} \boldsymbol {\Lambda }_h$
.
Let
![]() $k\in \{1,\dots , M\}$
be the unique integer such that
$k\in \{1,\dots , M\}$
be the unique integer such that
![]() $(i_0,j_0)\in E_k$
. Lemma 8.8 gives
$(i_0,j_0)\in E_k$
. Lemma 8.8 gives
![]() $\sum _{(i,j)\in E_k} \vert z_{i,n}\vert \vert z_{j,n} \vert e^{\zeta _4 L_{i,j}} \to 0$
. As the sequence of terms
$\sum _{(i,j)\in E_k} \vert z_{i,n}\vert \vert z_{j,n} \vert e^{\zeta _4 L_{i,j}} \to 0$
. As the sequence of terms
![]() $(z_{j,n})_{j\in I}$
is bounded by Theorem 8.1
$(z_{j,n})_{j\in I}$
is bounded by Theorem 8.1
![]() $(a)$
, we get
$(a)$
, we get
![]() $\vert z_{i,n}\vert \vert z_{j,n}\vert \to 0$
if either
$\vert z_{i,n}\vert \vert z_{j,n}\vert \to 0$
if either
![]() $i\notin E$
or
$i\notin E$
or
![]() $j\notin E$
. From the equality
$j\notin E$
. From the equality
we infer that
![]() $\sum _{(i,j)\in E_k \cap E^2} \vert z_{i,n}\vert \vert z_{j,n} \vert e^{\zeta _4 L_{i,j}} \to 0$
.
$\sum _{(i,j)\in E_k \cap E^2} \vert z_{i,n}\vert \vert z_{j,n} \vert e^{\zeta _4 L_{i,j}} \to 0$
.
Let
![]() $(i,j)\in E_k \cap E^2$
. As
$(i,j)\in E_k \cap E^2$
. As
![]() $(i_0, j_0)\in E_k \cap E^2$
, we have
$(i_0, j_0)\in E_k \cap E^2$
, we have
![]() $\boldsymbol {\Lambda }_{i_0,j_0}= \mathbf {c}_k = \boldsymbol {\Lambda }_{i,j}$
; whence
$\boldsymbol {\Lambda }_{i_0,j_0}= \mathbf {c}_k = \boldsymbol {\Lambda }_{i,j}$
; whence
The maximality of
![]() $\boldsymbol {\Lambda }_{j_0}$
, together with the minimality of
$\boldsymbol {\Lambda }_{j_0}$
, together with the minimality of
![]() $\boldsymbol {\Lambda }_{i_0}$
, shows that
$\boldsymbol {\Lambda }_{i_0}$
, shows that
![]() $\boldsymbol {\Lambda }_j= \boldsymbol {\Lambda }_{j_0}$
and
$\boldsymbol {\Lambda }_j= \boldsymbol {\Lambda }_{j_0}$
and
![]() $\boldsymbol {\Lambda }_i= \boldsymbol {\Lambda }_{i_0}$
. Since
$\boldsymbol {\Lambda }_i= \boldsymbol {\Lambda }_{i_0}$
. Since
![]() $\boldsymbol {\Lambda }_j$
are pairwise distinct when j ranges over all elements of I, we deduce that
$\boldsymbol {\Lambda }_j$
are pairwise distinct when j ranges over all elements of I, we deduce that
![]() $(i,j)=(i_0,j_0)$
, and so
$(i,j)=(i_0,j_0)$
, and so
![]() $E_k \cap E^2=\{(i_0,j_0)\}$
. But then,
$E_k \cap E^2=\{(i_0,j_0)\}$
. But then,
![]() $\vert z_{i_0,n} \vert \vert z_{j_0,n}\vert e^{\zeta _4 L_{i_0,j_0}} \to 0$
, i.e., either
$\vert z_{i_0,n} \vert \vert z_{j_0,n}\vert e^{\zeta _4 L_{i_0,j_0}} \to 0$
, i.e., either
![]() $z_{i_0,n} \to 0$
or
$z_{i_0,n} \to 0$
or
![]() $z_{j_0,n} \to 0$
, contradicting the definition of E. Theorem 8.1
$z_{j_0,n} \to 0$
, contradicting the definition of E. Theorem 8.1
![]() $(b)$
follows.
$(b)$
follows.
Acknowledgment
I thank Y. Bilu and M. Sombra for their helpful advice; F. Amoroso, L. Pottmeyer, G. Rémond, and the anonymous referees for their relevant suggestions; and S. Fischler for his help concerning Lemma 4.2.