Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-05T11:57:54.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and Sufficient Conditions for the Discreteness of the Spectrum of Certain Singular Differential Operators

Published online by Cambridge University Press:  20 November 2018

Calvin D. Ahlbrandt ,
Don B. Hinton  and
Roger T. Lewis
Calvin D. Ahlbrandt
Affiliation:
University of Missouri, Columbia, Missouri
Don B. Hinton
Affiliation:
University of Tennessee, Knoxville, Tennessee
Roger T. Lewis
Affiliation:
University of Alabama in Birmingham, Birmingham, Alabama
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Let P(x) be an m × m matrix-valued function that is continuous, real, symmetric, and positive definite for all x in an interval J , which will be further specified. Let w(x) be a positive and continuous weight function and define the formally self adjoint operator l by

where y(x) is assumed to be an m-dimensional vector-valued function. The operator l generates a minimal closed symmetric operator L0 in the Hilbert space ℒm2(J; w) of all complex, m-dimensional vector-valued functions y on J satisfying

with inner product

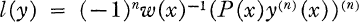
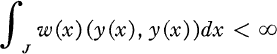
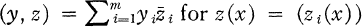where . All selfadjoint extensions of L0 have the same essential spectrum ([5] or [19]). As a consequence, the discreteness of the spectrum S(L) of one selfadjoint extension L will imply that the spectrum of every selfadjoint extension is entirely discrete.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 229 - 246
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Ahlbrandt, C. D., Equivalent boundary value problems for self adjoint differential systems, J. Differential Equations 9 (1971), 420–435.Google Scholar
2. Ahlbrandt, C. D., Disconjugacy criteria for self adjoint differential systems, J. Differential Equations 6 (1969), 271–295.Google Scholar
3. Ahlbrandt, C. D., Hinton, D. B. and Lewis, R. T., The effect of variable change on oscillation and disconjugacy criteria with applications to spectral theory and asymptotic theory, J. Math. Analysis and Applications, in press.Google Scholar
4. Sh. Birman, M., The spectrum of singular boundary-value problems, Matem. Sb. 55 (1961), 125–173.Google Scholar
5. Dunford, N. and Schwartz, J. T., Linear operators, II (Interscience, New York, 1948).Google Scholar
6. Glazman, I. M., Direct methods of qualitative spectral analysis of singular differential operators, Jerusalem: Israel Program for Scientific Translations (1965).Google Scholar
7. Hille, E., Nono sdilation theorems, Transactions Amer. Math. Soc. 64 (1948), 234–252.Google Scholar
8. Hinton, D. B. and Lewis, R. T., Oscillation theory at a finite singularity, J. Differential Equations 30 (1978), 235–247.Google Scholar
9. Hinton, D. B. and Lewis, R. T., Singular differential operators with spectra discrete and bounded below, Proc. Royal Society of Edinburgh 84A (1979), 117–134.Google Scholar
10. Kalyabin, G. A., A necessary and sufficient condition for the spectrum of a homogeneous operation to be discrete in the matrix case, Differential Equations 9 (1973), 951–954.Google Scholar
11. Leighton, W., On self adjoint differential equations of second order, J. London Math. Soc. 27 (1952), 37–47.Google Scholar
12. Lewis, R. T., Conjugate points of vector-matrix differential equations, Transactions Amer. Math. Soc. 231 (1977), 167–178.Google Scholar
13. Lewis, R. T., The discreteness of the spectrum of self adjoint, even order, one term, differential operators, Proc. Amer. Math. Soc. 42 (1974), 480–482.Google Scholar
14. Lewis, R. T., Oscillation and nonos dilation criteria for some self-adjoint, even order, linear differential operators, Pacific J. Math. 51 (1974), 221–234.Google Scholar
15. Lewis, R. T. and Wright, L. C., Comparison and oscillation criteria for selfadjoint vector-matrix differential equations, Pacific J. Math. 90 (1980), 125–134.Google Scholar
16. Martynov, V. V., The conditions for discreteness and continuity of the spectrum in case of a selfadjoint system of even order differential equations, Differential Equations 1 (1965), 1578–1591.Google Scholar
17. Moore, R. A., The behavior of solutions of a linear differential equation of second order, Pacific J. Math. 5 (1955), 125–145.Google Scholar
18. Miiller-Pfeiffer, E., Spektraleigenschaften Singuldrer Gewohnlicher Differentialoperatoren (Teubner-Texte zur Mathematik, Leipzig, 1977).Google Scholar
19. Naimark, M. A., Linear differential operators, II (Ungar, New York, 1968).Google Scholar
20. Reid, W. T., Ordinary differential equations (John Wiley and Sons, New York, 1971).Google Scholar
21. Wintner, A., A criterion of oscillatory stability, Quart. Appl. Math. 7 (1949), 115–117.Google Scholar