Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T05:21:53.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and Sufficient Conditions for Mean Convergence of Lagrange Interpolation for Erdős Weights II

Published online by Cambridge University Press:  20 November 2018

S. B. Damelin  and
D. S. Lubinsky
S. B. Damelin
Affiliation:
S. B. Damelin Department of Mathematics University of the Witwatersrand P.O. Wits 2050 Republic of South Africa, e-mail: [email protected]
D. S. Lubinsky
Affiliation:
D. S. Lubinsky Department of Mathematics University of the Witwatersrand P.O. Wits 2050 Republic of South Africa, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We complete our investigations of mean convergence of Lagrange interpolation at the zeros of orthogonal polynomials pn(W2, x) for Erdős weights W2 = e-2Q. The archetypal example is Wk,α = exp(—Qk,α), where

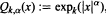
α > 1, k ≥ 1, and 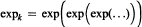is the k-th iterated exponential. Following is our main result: Let 1 < p < 4 and α ∊ ℝ Let Ln[f] denote the Lagrange interpolation polynomial to ƒ at the zeros of pn(W2, x) = pn(e-2Q, x). Then for

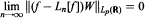
to hold for every continuous function ƒ:ℝ. —> ℝ satisfying

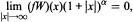
it is necessary and sufficient that α > 1/p. This is, essentially, an extension of the Erdös-Turan theorem on L2 convergence. In an earlier paper, we analyzed convergence for all p > 1, showing the necessity and sufficiency of using the weighting factor 1 + Q for all p > 4. Our proofs of convergence are based on converse quadrature sum estimates, that are established using methods of H. König.

Keywords

42C1542C0565D05Erdős weightsLagrange interpolationmean convergenceLp norms
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 4 , 01 August 1996 , pp. 737 - 757
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Clunie, J., Kovari, T., On integral functions having prescribed asymptotic growth II, Canad. J., Math. 20(1968), 7–20.Google Scholar
2. Damelin, S.B. and Lubinsky, D.S., Necessary and sufficient conditions for mean convergence of Lagrange interpolation for Erdȍs weights, Canad. J. Math., to appear.Google Scholar
3. Freud, G., Orthogonal polynomials, Pergamon Press/Akademiai Kiado, Budapest, 1970.Google Scholar
4. König, H. andNielson, N.J., Vector valued Lp convergence of orthogonal series and Lagrange interpolation, Forum, Math. 6(1994), 183–207.Google Scholar
5. Konig, H., Vector valued Lagrange interpolation and mean convergence of Hermite series, Proc. Essen Conference on Functional Analysis, North Holland, to appear.Google Scholar
6. Koosis, P., The logarithmic integral I, Cambridge University Press, Cambridge, 1988.Google Scholar
7. Levin, A.L., Lubinsky, D.S. and Mthembu, T.Z., Christoffel functions and orthogonal polynomials for Erdos weights on (-∞, ∞), Rend. Mat. Appl., (7) 14(1994), 199–289.Google Scholar
8. Lubinsky, D.S., The weighted Lp norms of orthonormal polynomials for Erdős weights, Comput. Math. Appl., to appear.Google Scholar
9. Lubinsky, D.S. and Mthembu, T.Z., Mean convergence of Lagrange interpolation for Erdos weights, J. Comput. Appl., Math. 47(1993), 369–390.Google Scholar
10. Mhaskar, H.N. and Saff, E.B., Where does the sup-norm of a weighted polynomial live?, Constr., Approx. 1(1985), 71–91.Google Scholar
11. Muckenhoupt, B., Mean convergence ofHermite andLaguerre series II, Trans. Amer. Math., Soc. 147(1970), 433–460.Google Scholar
12. Stein, E.M., Harmonic analysis: real variable methods, orthogonality and oscillatory integrals, Princeton University Press, Princeton, 1993.Google Scholar