No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In this paper the Corwin's conjecture is proved, which says that if d is a function analytic near ∞, then the hypoellipticity of the convolution operator Ad, defined by 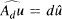 for every u ∊ S'(ℝn), implies that P(x)/ logx → ∞ as x → ∞, where P(x) is the distance from x ∊ ℝn to the set of complex zeros of d.
for every u ∊ S'(ℝn), implies that P(x)/ logx → ∞ as x → ∞, where P(x) is the distance from x ∊ ℝn to the set of complex zeros of d.
Supported by NNFC and Special Fund for Doctoral Program in University.