Article contents
Nearly Approximate Transitivity (AT) for Circulant Matrices
Published online by Cambridge University Press: 07 March 2019
Abstract
By previous work of Giordano and the author, ergodic actions of 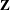 $\mathbf{Z}$ (and other discrete groups) are completely classified measure-theoretically by their dimension space, a construction analogous to the dimension group used in
$\mathbf{Z}$ (and other discrete groups) are completely classified measure-theoretically by their dimension space, a construction analogous to the dimension group used in 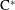 $\text{C}^{\ast }$-algebras and topological dynamics. Here we investigate how far from approximately transitive (AT) actions can be that derive from circulant (and related) matrices. It turns out not very: although non-AT actions can arise from this method of construction, under very modest additional conditions, approximate transitivity arises. KIn addition, if we drop the positivity requirement in the isomorphism of dimension spaces, then all these ergodic actions satisfy an analogue of AT. Many examples are provided.
$\text{C}^{\ast }$-algebras and topological dynamics. Here we investigate how far from approximately transitive (AT) actions can be that derive from circulant (and related) matrices. It turns out not very: although non-AT actions can arise from this method of construction, under very modest additional conditions, approximate transitivity arises. KIn addition, if we drop the positivity requirement in the isomorphism of dimension spaces, then all these ergodic actions satisfy an analogue of AT. Many examples are provided.
Keywords
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
Supported in part by an NSERC Discovery Grant.
References
- 1
- Cited by


