Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-02T22:28:18.078Z Has data issue: false hasContentIssue false
  • English
  • Français

The n-Dimensional Distributional Hankel Transformation

Published online by Cambridge University Press:  20 November 2018

E. L. Koh
E. L. Koh*
Affiliation:
University of Regina, Regina, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Hankel transformation was extended to certain generalized functions of one dimension [1; 2; 3]. In this paper, we develop the n-dimensional case corresponding to [1]. The procedure in [1] is briefly as follows:

A test function space Hμ is constructed on which the μth order Hankel transformation hμ defined by

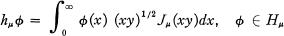
is an automorphism whenever μ ≧ —1/2. The generalized transformation hμ' is then defined on the dual Hμ' as the adjoint of hμ through a Parseval relation, i.e.

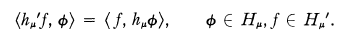
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 2 , 01 April 1975 , pp. 423 - 433
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Zemanian, A. H., A distributional Hankel transformation, SI AM J. Appl. Math. 14 (1966), 561–576.Google Scholar
2. Koh, E. L. and Zemanian, A. H., The complex Hankel and I-transformations of generalized functions, SIAM J. Appl. Math. 16 (1968), 945–957.Google Scholar
3. Koh, E. L., The Hankel transformation of negative order for distributions of rapid growth, SIAM J. Math. Anal. 1 (1970), 322–327.Google Scholar
4. Zemanian, A. H., Generalized integral transformations (Interscience, New York, 1968).Google Scholar
5. Fleming, W. H., Functions of several variables (Addison-Wesley, Reading, Mass, 1965).Google Scholar
6. Sneddon, I.N., Fourier transforms (McGraw-Hill, New York, 1951).Google Scholar