Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-04T18:47:30.185Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Mixing and Rank One Group Actions

Published online by Cambridge University Press:  20 November 2018

Andrés del Junco  and
Reem Yassawi
Andrés del Junco
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 1A1
Reem Yassawi
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montreal, QC, H3A 2K6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose $G$ is a countable, Abelian group with an element of infinite order and let 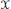$\text{ }\!\!\chi\!\!\text{ }$ be a mixing rank one action of $G$ on a probability space. Suppose further that the Følner sequence 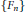$\{{{F}_{n}}\}$ indexing the towers of 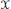$\text{ }\!\!\chi\!\!\text{ }$ satisfies a “bounded intersection property”: there is a constant 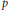$p$ such that each 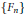$\{{{F}_{n}}\}$ can intersect no more than 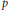$p$ disjoint translates of 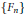$\{{{F}_{n}}\}$. Then 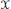$\text{ }\!\!\chi\!\!\text{ }$ is mixing of all orders. When 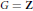$G\,=\,\mathbf{Z}$, this extends the results of Kalikow and Ryzhikov to a large class of “funny” rank one transformations. We follow Ryzhikov’s joining technique in our proof: the main theorem follows from showing that any pairwise independent joining of 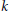$k$ copies of 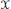$\text{ }\!\!\chi\!\!\text{ }$ is necessarily product measure. This method generalizes Ryzhikov’s technique.

Keywords

28D15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 2 , 01 April 2000 , pp. 332 - 347
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Blum, J. R. and Hanson, D. L., On the mean ergodic theorem for subsequences. Bull. Amer. Math. Soc. 66(1960), 308–311.Google Scholar
[2] Ferenczi, S., Systèmes de rang un gauche. Ann. Inst. Henri Poincaré (2) 21(1985), 177–186.Google Scholar
[3] Host, B., Mixing of all orders and pairwise independent joinings of systems with singular spectrum. Israel J. Math 76(1991), 289–298.Google Scholar
[4] del Junco, A., A weakly mixing simple map with no prime factors. Israel J. Math., to appear.Google Scholar
[5] del Junco, A., A Transformation with Simple Spectrum which is not Rank One. Canad. J. Math. (3) 29(1977), 655–663.Google Scholar
[6] del Junco, A. and Rudolph, D., On ergodic actions whose self-joinings are graphs. Ergodic Theory Dynamical Systems 7(1987), 531–557.Google Scholar
[7] Kalikow, S. A., Twofold mixing implies threefold mixing for rank one transformations. Ergodic Theory Dynamical Systems 4(1984), 237–259.Google Scholar
[8] Ornstein, D. and Weiss, B., The Shannon-McMillan-Breiman theorem for amenable groups. Israel J. Math. (1) 44(1983), 53–60.Google Scholar
[9] Rokhlin, V. A., On ergodic compact Abelian groups. Izv. Akad. Nauk. SSSR Ser. Mat. 13(1949), 323–340.(Russian).Google Scholar
[10] Ryzhikov, V. V., Mixing, Rank, andMinimal Self-Joining of Actions with an Invariant Measure. Russian Acad. Sci. Sb. Math. (2) 75(1993), 405–427.Google Scholar
[11] Ryzhikov, V. V., Joinings and multiple mixing of the actions of finite rank. Funct. Anal. Appl. 27(1993), 128–140.Google Scholar
[12] Tempel’man, A. A., Ergodic Theorems for General Dynamical Systems. English transl.: Soviet Math. Doklady (5) 8(1967), 1213–1216.Google Scholar