Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T12:17:44.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone Classes of Dendrites

Published online by Cambridge University Press:  20 November 2018

Veronica Martínez-de-la-Vega  and
Christopher Mouron
Veronica Martínez-de-la-Vega
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México Circuito exterior, Cd. Universitaria, México D.F., 04510, Mexico e-mail: [email protected]
Christopher Mouron
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México Circuito exterior, Cd. Universitaria, México D.F., 04510, Mexico e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Continua $X$ and 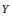$Y$ are monotone equivalent if there exist monotone onto maps 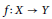$f\,:\,X\,\to \,Y$ and 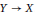$g:\,Y\to \,X.\,\text{A}$ . A continuum $X$ is isolated with respect to monotone maps if every continuumthat is monotone equivalent to $X$ must also be homeomorphic to $X$ . In this paper we show that a dendrite $X$ is isolated with respect to monotone maps if and only if the set of ramification points of $X$ is finite. In this way we fully characterize the classes of dendrites that are monotone isolated.

Keywords

54F5054C1006A0754F1554F6503E15dendritemonotonebqoantichain
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 3 , 01 June 2016 , pp. 675 - 697
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Camerlo, R., Darji, U. B., and Marcone, A., Classification problems in continuum theory. Trans. Amer. Math. Soc. 357(2005), no. 11, 4301–4328. http://dx.doi.org/10.1090/S0002-9947-05-03956-5 Google Scholar
[2]Charatonik, J. J.,Monotone mappings of universal dendrites. Topology Appl. 38(1991), no. 2,163–187. http://dx.doi.org/10.1016/0166-8641(91)90083-X Google Scholar
[3]Laver, R., Order types and well-quasi-orderings. Thesis (Ph.D.), University of California, Berkeley,1969.Google Scholar
[4] Laver, R., On Fraïssé's order type conjecture. Ann. of Math. (2)93(1971), 89–111.http://dx.doi.org/10.2307/1970754 Google Scholar
[5] Martínez de la Vega, V. and Martínez Montejano, J., Open problems on dendroids. In: Open Problems in Topology. II, Elsevier, 2007, pp. 319–334 Google Scholar
[6] Menger, K., Kurventheorie, Teubner, Leipzig, 1932.Google Scholar
[7] Nash-Williams, C. St. J. A., On well-quasi-ordering inûnite trees. Proc.Cambridge Philos. Soc. 61(1965), 697–720. http://dx.doi.org/10.1017/S0305004100039062 Google Scholar
[8] Rado, R., Partial well-ordering of sets of vectors. Mathematika 1(1954), 89–95. http://dx.doi.org/10.1112/S0025579300000565 Google Scholar
[9] Ważewski, T., Sur les courbes de Jordan ne renferment aucune courbe simple fermée de Jordan. Ann. Soc. Pol. Math2(1293), 49–170. Google Scholar