Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-15T22:14:28.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Monochromatic Solutions to 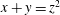$x+y=z^{2}$

Part of: Sequences and sets Extremal combinatorics

Published online by Cambridge University Press:  07 January 2019

Ben Joseph Green  and
Sofia Lindqvist
Ben Joseph Green
Affiliation:
Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG Email: ben.green@maths.ox.ac.uklindqvist.sofia@gmail.com
Sofia Lindqvist
Affiliation:
Mathematical Institute, Radcliffe Observatory Quarter, Woodstock Rd, Oxford OX2 6GG Email: ben.green@maths.ox.ac.uklindqvist.sofia@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that N is 2-coloured. Then there are infinitely many monochromatic solutions to 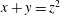$x+y=z^{2}$. On the other hand, there is a 3-colouring of N with only finitely many monochromatic solutions to this equation.

Keywords

additive combinatoricsRamsey theory

MSC classification

Primary: 11B75: Other combinatorial number theory
Secondary: 05D10: Ramsey theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 3 , June 2019 , pp. 579 - 605
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was partially supported by a grant from the Simons Foundation (award number 376201 to Ben Green) , and the first author is supported by ERC Advanced Grant AAS 279438. We thank both organisations for their support.

References

Bombieri, E., Friedlander, J. B., and Iwaniec, H., Primes in arithmetic progressions to large moduli . II. Math. Ann. 277(1987), no. 3, 361–393. https://doi.org/10.1007/BF01458321.Google Scholar
Eberhard, S., The abelian arithmetic regularity lemma. arixv:1606.09303.Google Scholar
Eberhard, S., Green, B., and Manners, F., Sets of integers with no large sum-free subset . Ann. of Math. (2) 180(2014), no. 2, 621–652. https://doi.org/10.4007/annals.2014.180.2.5.Google Scholar
Green, B., A Szemerédi-type regularity lemma in abelian groups, with applications . Geom. Funct. Anal. 15(2005), no. 2, 340–376. https://doi.org/10.4007/annals.2012.175.2.2.Google Scholar
Green, B. and Tao, T., An arithmetic regularity lemma, an associated counting lemma, and applications . In: An irregular mind, Bolyai Soc. Math. Stud., 21, János Bolyai Math. Soc., Budapest, 2010, pp. 261–334.. https://doi.org/10.1007/978-3-642-14444-8_7.Google Scholar
Green, B. and Tao, T., The quantitative behaviour of polynomial orbits on nilmanifolds . Ann. of Math. (2) 175(2012), no. 2, 465–540. https://doi.org/10.4007/annals.2012.175.2.2.Google Scholar
Gyarmati, K., Csikvári, P., and Sárközy, A., Density and Ramsey type results on algebraic equations with restricted solution sets . Combinatorica 32(2012), 425–449. https://doi.org/10.1007/s00493-012-2697-9.Google Scholar
Katznelson, Y., An introduction to harmonic analysis . Second Ed. Dover Publications, Inc., New York, 1976.Google Scholar
Khalfallah, A. and Szemerédi, E., On the number of monochromatic solutions of x + y = z 2 . Combin. Probab. Comput. 15(2006), no. 1–2, 213–227. https://doi.org/10.1017/S0963548305007169.Google Scholar
Lagarias, J. C., Odlyzko, A. M., and Shearer, J. B., On the density of sequences of integers the sum of no two of which is a square. I. Arithmetic progressions . J. Combin. Theory Ser. A 33(1982), no. 2, 167–185. https://doi.org/10.1016/0097-3165(82)90005-X.Google Scholar
Lagarias, J. C., Odlyzko, A. M., and Shearer, J. B., On the density of sequences of integers the sum of no two of which is a square. II. General sequences . J. Combin. Theory Ser. A 34(1983), no. 2, 123–139. https://doi.org/10.1016/0097-3165(83)90051-1.Google Scholar
Lindqvist, S., Partition regularity of generalised Fermat equations. arxiv:1606.07334.Google Scholar
Lindqvist, S., Monochromatic solutions to $x+y$ a square in $Z/qZ$ , http://people.maths.ox.ac.uk/lindqvist/notes/xysumsquare.pdf.Google Scholar
Montgomery, H. L., Ten lectures on the interface between analytic number theory and harmonic analysis. CBMS Regional Conference Series in Mathematics, 84, Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1994. https://doi.org/10.1090/cbms/084.Google Scholar
Vaughan, R. C., The Hardy-Littlewood method. Cambridge Tracts in Mathematics, 125, Cambridge University Press, Cambridge, 1997. https://doi.org/10.1017/CBO9780511470929.Google Scholar
Wooley, T. D., On Diophantine inequalities: Freeman’s asymptotic formulae. In: Proceedings of the Session in Analytic Number Theory and Diophantine Equations, Bonner Math. Schriften, 360, Univ. Bonn, Bonn, 2003.Google Scholar