Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-19T02:43:37.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Moments of the Critical Values of Families of Elliptic Curves, with Applications

Published online by Cambridge University Press:  20 November 2018

Matthew P. Young
Matthew P. Young*
Affiliation:
American Institute of Mathematics, Palo Alto, CA 94306-2244, U.S.A. and Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, U.S.A.
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We make conjectures on the moments of the central values of the family of all elliptic curves and on the moments of the first derivative of the central values of a large family of positive rank curves. In both cases the order of magnitude is the same as that of the moments of the central values of an orthogonal family of $L$-functions. Notably, we predict that the critical values of all rank 1 elliptic curves is logarithmically larger than the rank 1 curves in the positive rank family.

Furthermore, as arithmetical applications, we make a conjecture on the distribution of 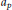${{a}_{p}}$'s amongst all rank 2 elliptic curves and show how the Riemann hypothesis can be deduced from sufficient knowledge of the first moment of the positive rank family (based on an idea of Iwaniec).

Keywords

11M4111G4011M26
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 1155 - 1181
Copyright
Copyright © Canadian Mathematical Society 2010

Footnotes

This research was supported by an NSF Mathematical Sciences Post-Doctoral Fellowship and by the American Institute of Mathematics.

References

[B MSW] Bektemirov, B., Mazur, B., Stein, W., and Watkins, M., Average ranks of elliptic curves: tension between data and conjecture. Bull. Amer. Math. Soc. (N.S.) 44(2007), no. 2, 233–254. doi:10.1090/S0273-0979-07-01138-XGoogle Scholar
[B] Birch, B., How the number of points of an elliptic curve over a fixed prime field varies. J. London Math. Soc. 43(1968), 57-60. doi:10.1112/jlms/s1-43.1.57Google Scholar
[BCDT] Breuil, C., Conrad, B., Diamond, F., and Taylor, R., On the modularity of elliptic curves over Q: wild 3-adic exercises. J. Amer. Math. Soc. 14(2001), no. 4, 843–939. doi:10.1090/S0894-0347-01-00370-8Google Scholar
[C] Conrey, J., The Riemann hypothesis. Notices Amer. Math. Soc. 50(2003), no. 3, 341–353.Google Scholar
[CFKRS] Conrey, J., Farmer, D., Keating, J., Rubinstein, M., and Snaith, N., Integral moments of L-functions. Proc. London Math. Soc. (3) 91(2005), no. 1, 33–104. doi:10.1112/S0024611504015175Google Scholar
[CKRS] Conrey, J. B., Keating, J., Rubinstein, M., and Snaith, N., On the frequency of vanishing of quadratic twists of modular L-functions. In: Number theory for the millennium, I (Urbana, IL, 2000), A K Peters, Natick, MA, 2002, pp. 301–315.Google Scholar
[F] Farmer, D.W., Modeling families of L-functions. In: Ranks of elliptic curves and random matrix theory, London Mathematical Society Lecture Note Series, 341, Cambridge University Press, Cambridge, 2007.Google Scholar
[GR] Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products. Fourth edition, Academic Press, New York, 1965.Google Scholar
[KS] Keating, J. P. and Snaith, N., Random matrix theory and L-functions at s = 1/2. Comm. Math. Phys. 214(2000), no. 1, 91–110. doi:10.1007/s002200000262Google Scholar
[Kn] Knapp, A.W., Elliptic curves. Mathematical Notes, 40, Princeton University Press, Princeton, NJ, 1992.Google Scholar
[M] Miller, S. J., Investigations of zeros near the central point of elliptic curve L-functions.With an appendix by Eduardo Due˜nez. Experiment. Math. 15(2006), no. 3, 257–279.Google Scholar
[Sch] Schoof, R., Nonsingular plane cubic curves over finite fields. J. Combin. Theory Ser. A 46(1987), no. 2, 183–211. doi:10.1016/0097-3165(87)90003-3Google Scholar
[Se] Selberg, A., Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series. J. Indian Math. Soc. 20(1956), 47–87.Google Scholar
[Si] Silverman, J. H., The arithmetic of elliptic curves. Graduate Texts in Mathematics, 106, Springer-Verlag, New York, 1986.Google Scholar
[Si2] Silverman, J. H., Advanced topics in the arithmetic of elliptic curves. Graduate Texts in Mathematics, 151, Springer-Verlag, New York, 1994.Google Scholar
[TW] Taylor, R. and Wiles, A., Ring-theoretic properties of certain Hecke algebras. Ann. of Math. (2) 141(1995), no. 3, 553–572. doi:10.2307/2118560Google Scholar
[Wa] Watkins, M., Some heuristics about elliptic curves. Experiment Math. 17(2008), no. 1, 105–125.Google Scholar
[Wi] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. (2) 141(1995), no. 3, 443–551. doi:10.2307/2118559Google Scholar
[Y2] Young, M., On the non-vanishing of elliptic curve L-functions at the central point. Proc. London Math. Soc. (3) 93(2006), no. 1, 1–42. doi:10.1017/S0024611506015760Google Scholar