Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-19T03:02:11.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Moduli Spaces of Reflexive Sheaves of Rank 2

Published online by Cambridge University Press:  20 November 2018

Jan O. Kleppe
Jan O. Kleppe*
Affiliation:
Oslo University College, Faculty of Engineering, Pb. 4 St. Olavs plass, 0130, Oslo, Norway
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 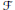$\mathcal{F}$ be a coherent rank 2 sheaf on a scheme $Y\,\subset \,{{\mathbb{P}}^{n}}$ of dimension at least two and let 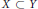$X\,\subset \,Y$ be the zero set of a section 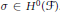$\sigma \,\in \,{{H}^{0}}\left( \mathcal{F} \right)$. In this paper, we study the relationship between the functor that deforms the pair 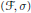$\left( \mathcal{F},\,\sigma \right)$ and the two functors that deform 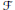$\mathcal{F}$ on 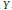$Y$, and 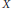$X$ in 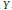$Y$, respectively. By imposing some conditions on two forgetful maps between the functors, we prove that the scheme structure of e.g., the moduli scheme 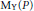${{\text{M}}_{\text{Y}}}\left( P \right)$ of stable sheaves on a threefold 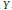$Y$ at $\left( \mathcal{F} \right)$, and the scheme structure at (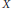$X$) of the Hilbert scheme of curves on 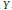$Y$ become closely related. Using this relationship, we get criteria for the dimension and smoothness of 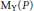${{\text{M}}_{\text{Y}}}\left( P \right)$ at $\left( \mathcal{F} \right)$, without assuming $\text{Ex}{{\text{t}}^{2}}\left( \mathcal{F},\,\mathcal{F} \right)\,=\,0$. For reflexive sheaves on $Y\,=\,{{\mathbb{P}}^{3}}$ whose deficiency module 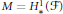$M\,=\,H_{*}^{1}\left( \mathcal{F} \right)$ satisfies 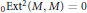$_{0}\text{Ex}{{\text{t}}^{2}}\left( M,\,M \right)\,=\,0$ (e.g., of diameter at most 2), we get necessary and sufficient conditions of unobstructedness that coincide in the diameter one case. The conditions are further equivalent to the vanishing of certain graded Betti numbers of the free graded minimal resolution of 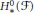$H_{*}^{0}\left( \mathcal{F} \right)$. Moreover, we show that every irreducible component of 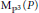${{\text{M}}_{\mathbb{P}}}^{3}\left( P \right)$ containing a reflexive sheaf of diameter one is reduced (generically smooth) and we compute its dimension. We also determine a good lower bound for the dimension of any component of 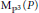${{\text{M}}_{\mathbb{P}}}^{3}\left( P \right)$ that contains a reflexive stable sheaf with “small” deficiency module $M$.

Keywords

14C0514D2214F0514J1014H5014B1013D0213D07moduli spacereflexive sheafHilbert schemespace curveBuchsbaum sheafunobstructednesscup productgraded Betti numbers
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 1131 - 1154
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Ancona, V. and Ottaviani, G., On singularities of MP3 (c1, c2). Internat. J. Math. 9(1998), no. 4, 407–419. doi:10.1142/S0129167X98000178Google Scholar
[2] Chang, M-C., A Filtered Bertini-type theorem. J. Reine Angew. Math. 397(1989), 214–219.Google Scholar
[3] Chang, M-C., Stable rank 2 reflexive sheaves on P3 with large c3. J. Reine Angew. Math. 343(1983), 99–107.Google Scholar
[4] Chang, M-C., Stable rank 2 reflexive sheaves on P3 with small c2 and applications. Trans. Amer. Math. Soc. 284(1984), no. 1, 57–89. doi:10.2307/1999274Google Scholar
[5] Ellia, P. and Fiorentini, M., Défaut de postulation et singularités du schéma de Hilbert. Ann. Univ. Ferrara Sez. VII 30(1984), 185–198.Google Scholar
[6] Ellingsrud, G. and Strømme, S. A., Stable rank 2 vector bundles with c1 = 0 and c2 = 3. Math. Ann. 255(1981), no. 1, 123–135. doi:10.1007/BF01450561Google Scholar
[7] Ellingsrud, G., Sur le schéma de Hilbert des variétés de codimension 2 dans Pe á cône de Cohen-Macaulay. Ann. Sci. École Norm. Sup. 8(1975), no. 4, 423–431.Google Scholar
[8] Guffroy, S., Dimension des familles de courbes lisses sur une surface quartique normales de P3. Proc. Amer. Math. Soc. 135(2007), no. 11, 3499–3505. doi:10.1090/S0002-9939-07-08966-6Google Scholar
[9] Gurrola, P. and Miró-Roig, R. M.. On the existence of generically smooth components for moduli spaces of rank 2 stable reflexive sheaves on P3. J. Pure Appl. Algebra 102(1995), no. 3, 313–345. doi:10.1016/0022-4049(94)00089-2Google Scholar
[10] Fløystad, G., Determining obstructions for space curves, with application to nonreduced components of the Hilbert scheme. J. Reine Angew. Math. 439(1993), 11–44.Google Scholar
[11] Grothendieck, A., Cohomologie locale des faisceaux cohérents et Théorèmes de Lefschetz locaux et globaux (SGA 2). Advanced Studies in Pure Mathematics, 2, North-Holland Publishing Co., Amsterdam, 1968.Google Scholar
[12] Grothendieck, A., Techniques de constructions et théorèmes d’existence en géométrie algébrique IV: les schémas de Hilbert. Séminaire Bourbaki, 6(1960), no. 221, 249–276.Google Scholar
[13] Hartshorne, R., Stable vector bundles of rank 2 on P3. Math. Ann. 238(1978), no. 3, 229–280. doi:10.1007/BF01420250Google Scholar
[14] Hartshorne, R., Stable reflexive sheaves. Math. Ann. 254(1980), no. 2, 121–176. doi:10.1007/BF01467074Google Scholar
[15] Hartshorne, R. and Sols, I., Stable rank 2 vector bundles on P3 with c1 = −1, c2 = 2. J. Reine Angew. Math. 325(1981), 145–152.Google Scholar
[16] Huybrechts, D. and Lehn, M., The Geometry of moduli spaces of sheaves. Aspects of Mathematics, E31, Friedr. Vieweg & Sohn, Braunschweig, 1997.Google Scholar
[17] Iliev, A. and Markushevich, D., Quartic 3-fold: pfaffians, vector bundles, and half-canonical curves. Michigan Math. J. 47(2000), no. 2, 385–394. doi:10.1307/mmj/1030132542Google Scholar
[18] Kleppe, J. O., Deformations of reflexive sheaves of rank 2 on P3. Preprint, University of Oslo, 1982, http://www.iu.hio.no/-jank/papers.htm Google Scholar
[19] Kleppe, J. O., Nonreduced components of the Hilbert scheme of smooth space curves. In: Space curves (Rocca di Papa), Lectures Notes in Math., 1266, Springer, Berlin, 1987, pp. 181–207.Google Scholar
[20] Kleppe, J. O., Liaison of families of subschemes in Pn. In: Algebraic curves and projective geometry (Trento, 1988), Lectures Notes in Math., 1389, Springer, Berlin, 1989, pp. 128–173.Google Scholar
[21] Kleppe, J. O., Concerning the existence of nice components in the Hilbert scheme of curves in Pn for n = 4 and 5. J. Reine Angew. Math. 475(1996), 77–102.Google Scholar
[22] Kleppe, J. O., The Hilbert scheme of space curves of small diameter. Ann. Inst. Fourier 56(2006), no. 5, 1297–1335.Google Scholar
[23] Laudal, O. A., Formal moduli of algebraic structures. Lectures Notes in Math., 754, Springer, Berlin, 1979.Google Scholar
[24] Laudal, O. A., A generalized trisecant lemma. In: Algebraic geometry (Proc. Sympos. Univ. Tromsø, 1977), Lectures Notes in Math., 687, Springer, Berlin, 1978. pp. 112–149.Google Scholar
[25] Laudal, O. A., Matrix massey products and formal moduli I. In: Algebra, algebraic topology and their interactions, Lecture Notes in Math., 1183, Springer, Berlin, 1986, pp. 218–240.Google Scholar
[26] Martin-Deschamps, M. and Perrin, D., Sur la classification des courbes gauches. Astérisque, 184–185, 1990.Google Scholar
[27] Maruyama, M., Moduli of stable sheaves. I. J. Math. Kyoto Univ. 17(1977), no. 1, 91–126.Google Scholar
[28] Maruyama, M., Moduli of stable sheaves. II. J. Math. Kyoto Univ. 18(1978), no. 3, 557–614.Google Scholar
[29] Meseguer, J., Sols, I., and Strømme, S. A., Compactification of a family of vector bundles on P3. In: 18th Scandinavian Congress of Mathematicians (Aarhus, 1980), Prog. Math, 11, Birkhäuser Boston, Inc., Boston, MA, 1981, pp. 474–494.Google Scholar
[30] Migliore, J. C., Introduction to liaison theory and deficiency modules. Progress in Math., 165, Birkhäuser Boston, Inc., Boston, MA, 1998.Google Scholar
[31] Miró-Roig, R. M., Gaps in the Chern classes of rank 2 stable reflexive sheaves. Math. Ann. 270(1985), no. 3, 317–323. doi:10.1007/BF01473429Google Scholar
[32] Miró-Roig, R. M., Faisceaux réflexifs stables de rang 2 sur P3 non obstrués. C. R. Acad. Sci. Paris Sér. I Math. 303(1986), no. 14, 711–713.Google Scholar
[33] Miró-Roig, R. M., Some moduli spaces for rank 2 stable reflexive sheaves on P3. Trans. Amer. Math. Soc 299(1987), no. 2, 699–717. doi:10.2307/2000521Google Scholar
[34] Miró-Roig, R. M., Singular moduli spaces of stable vector bundles on P3. Pacific J. Math. 172(1996), no. 2, 477–482.Google Scholar
[35] Miró-Roig, R. M. and Trautmann, G., The moduli scheme M(0, 2, 4) over P3. Math. Z. 216(1994), no. 2, 283–315. doi:10.1007/BF02572323Google Scholar
[36] Mumford, D., Further pathologies in algebraic geometry. Amer. J. Math. 84(1962), 642–648. doi:10.2307/2372870Google Scholar
[37] Nasu, H., Obstructions to deforming space curves and non-reduced components of the Hilbert scheme. Publ. Res. Inst. Math. Sci. 42(2006), no. 1, 117–141. doi:10.2977/prims/1166642061Google Scholar
[38] Rao, A. P., Liaison among curves in P3. Invent. Math. 50(1978/79), no. 3, 205–217. doi:10.1007/BF01410078Google Scholar
[39] Roggero, M., Valabrega, P., and Valenzano, M., Rank two bundles and reflexive sheaves on P3 and corresponding curves: an overview. In: Geometric and combinatorial aspects of commutative algebra ( Messina 1999), Lecture Notes in Pure and Appl. Math., 217, Dekker, New York, 2001, pp. 327–343.Google Scholar
[40] Schlessinger, M., Functors of Artin rings. Trans. Amer. Math. Soc. 130(1968), 208–222. doi:10.2307/1994967Google Scholar
[41] Sernesi, E., An example of an obstructed curve in P3. (Italian) In: Semimar on complex variable (Bologna, 1981), CNR, Rome, 1982, pp. 223–231.Google Scholar
[42] Strømme, S. A., Ample divisors on fine moduli spaces on the projective plane. Math. Z. 187(1984), no. 3, 405–423. doi:10.1007/BF01161956Google Scholar
[43] Vakil, R., Murphy's law in algebraic geometry: badly-behaved deformation spaces. Invent. Math. 164(2006), no. 3, 569–590. doi:10.1007/s00222-005-0481-9Google Scholar
[44] Valenzano, M., Rank 2 reflexive sheaves on a smooth threefold. Rend. Sem. Mat. Univ. Pol. Torino 62(2004), no. 3, 235–254.Google Scholar
[45] Vermeire, P., Moduli of reflexive sheaves on smooth projective 3-fold. J. Pure Appl. Algebra 211(2007), no. 3, 622–632. doi:10.1016/j.jpaa.2007.03.006Google Scholar
[46] Vogelaar, J. A., Constructing vector bundles from codimension two subvarieties. Ph.D. Thesis, Leiden, 1978.Google Scholar
[47] Walter, C., Some examples of obstructed curves in P3. In: Complex projective geometry, London Math. Soc. Lecture Note Ser., 179, Cambridge University Press, Cambridge, 1992, pp. 324–340.Google Scholar
[48] Weibel, C. A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, Cambridge, 1994.Google Scholar